论文《PMSC: PatchMatch-Based Superpixel Cut for Accurate Stereo Matching》学习

Abstract

(2018 一区)在立体匹配问题中，同时估计一个像素的视差和法向，而不仅仅是视差，也被称为3D标记方法，可以获得更高的亚像素精度。然而，由于参数空间的无限性，在保持全局一致性的同时，给来自连续标签空间R 3的每个像素分配合适的3D标签是极其困难的。本文提出了一种新的基于补丁匹配的超像素切割算法，以更准确地分配图像的三维标签。为了在本地窗口之间实现稳健而精确的立体匹配，我们提出了一种双层匹配代价，利用自底向上的方法来设计两层。利用预先训练好的卷积神经网络，利用底层对局部小正方形斑块之间的相似性进行度量，然后利用顶层对由物体表面切平面引起的大不规则窗口的局部匹配代价进行集合。为了优化局部赋值的空间平滑性，我们提出了一种更新3D标签的新策略。在优化过程中，利用PatchMatch的分割信息和随机细化的方法，对每个像素的候选3D标签集进行更新，从而获得更低的概率损失。自成对的能量一般候选材料-日期标签集违反的子模块属性图,我们提出了一种新型多层superpixel结构将候选标签集分组为候选人作业,从而可以有效地融合了α-expansion图。大量的实验证明，我们的方法可以在不同的数据集上获得更高的亚像素精度，目前在新的具有挑战性的Middlebury 3.0基准测试中，我们的方法在所有现有方法中排名第一。
索引术语- 3d标签，补丁匹配，立体匹配，超像素切割(SC)。

1. Introduction

立体匹配一直是计算机视觉的核心问题之一。近年来，3D标签的广泛应用在很大程度上提高了立体匹配算法的精度。3D标签方法不需要分配一个离散的视差值，而是为每个像素分配三个连续的值，同时表示视差和表面法线方向，具有以下优点。首先，他们避免了在1D标签立体声方法中常见的“阶梯效应”的前端平行排列偏差。其次，利用曲面法线确定倾斜曲面的对应区域是合理的。第三，仅用[2]对约束，即可得到视差的二阶光滑性。

然而，由于三维标签具有巨大的连续标签空间$R^3$和非凸能量函数，因此无论是成本聚合还是全局优化都不如标量视差情况那样简单。为了更好地克服上述使用3D标签的困难，我们提出了一种基于patch的超像素切割(superpixel cut, PMSC)算法来进行精确的立体匹配。

第一个挑战是patch匹配成本的选择。对于标签诱导的一维正方形patch，我们已经精心设计了大量的匹配代价[3]-[7]，但是在每个匹配窗口中视差值不变的假设使得窗口很小，唯一性较弱。使用3D标签诱导的斜斑块克服了前端并行假设的不利条件，因此窗口大小通常大得多。然而，由于不同3D标签的匹配窗口形状不同，将最先进的匹配成本从前端平行补片扩展到倾斜补片通常是低效的。因此，现有的倾斜patch的匹配代价通常是通过像素强度和梯度差值的直接累加来计算的，这对于很多具有挑战性的情况是不适用的，比如左右图像之间的曝光或者光照变化。

为了解决这个问题，我们提出了一种双层策略来构造新的匹配代价。首先利用预训练卷积神经网络（CNN）[5]预测小额额侧窗的相似性，然后在3D标签诱导的大斜窗上用自适应权值[8]对像素相似性进行聚集。第一层提高了局部匹配的鲁棒性，在小的正方形窗口上可以忽略前面平行假设误差，而第二层保证了大的倾斜窗口上与倾斜物体表面的一致性。

第二个挑战是如何对每个像素的无限3D标签空间进行全局优化。一个有效的解决方法是使用分割作为硬约束或软约束[9]-[13]。在对强度图像进行过分割后，基于分割的方法在超像素水平上计算候选的三维标签，假设同一段内的像素属于同一三维表面。然后从有限标签集而不是整个标签空间$R^3$中找到最佳赋值。虽然超像素级的处理复杂度较低，但由于候选3D标签集不足，精度受到限制，优化过程中可能会出现分割错误。另一组方法借鉴了PatchMatch[14]的思想，用于近似最近邻字段。PatchMatch立体声[1]通过随机采样和邻居传播的方式减少了巨大的搜索空间，并直接从$R^3$中为每个像素分配一个近似最佳的3D标签。随后，不同的正则化项[15]-[19]被加入到结构全局方法中。全局PatchMatch方法虽然达到了更高的精度，但其优化过程却很容易陷入虚假的局部极小值。此外，每个像素的极度冗余采样和传播使得高分辨率图像的运行时间很快变得不可接受。为了充分利用基于分段的方法的效率和基于补丁的方法的准确性，我们提出了一种新的全局优化策略。基于groundtruth标记通常是空间平滑的，并且在对象边缘处存在不连续，我们执行了多层超像素分割，并沿着超像素迭代地传播候选标签。我们还使用了PatchMatch的随机细分来更新每个像素的候选标签集，我们希望从中找到整个图像更好的分配。自解决常见的优化,比如融合移动[20]或[21]信仰传播原始候选标签集不够准确和高效,我们重组候选标签设置为候选人全球作业叫建议采用α-expansion图切为优化[22]。提出了一种基于区域腐蚀的超像素图像超像素建议构造方法，满足了图割的子模块要求。

总的来说，我们的贡献主要有以下四个方面：

• 我们提出了一个有效的三维像素标签优化框架，通过迭代生成和融合超像素建议。
• 结合基于cnn和基于patchmatch的相似性度量，我们提出了一种3D标签的双层匹配成本。
• 我们设计一种新型superpixel提议结构,所以α-expansion图的子模块的需求减少会融合。
• 在视差图精度方面，该方法在新的Middlebury 3.0基准测试中排名第一，并优于其他全局PatchMatch方法。

三维标签的匹配成本计算不同于离散差异的匹配成本计算。每个像素点对应的不规则区域是由物体表面的切平面引起的，切平面随三维标签的不同而变化。在这种情况下，基于分段的方法综合了超级混合体内部的强度和梯度差异[9]，而基于补丁匹配的方法则在倾斜的补丁内部使用自适应权重进行聚合[1]。为了更好的处理曝光和光照变化，Zhang等人[11]和Yamaguchi等人[23]将像素之间的强度和梯度差异替换为梯度，并将小块正方形斑块之间的普查变换差异替换为匹配成本，但匹配成本仅针对超像素进行计算。Zbontar和LeCun[5]使用CNN来提高方形斑块匹配的准确性，而前端并行成本聚合仅在离散的差值上。与上述方法不同的是，我们的双层匹配算法既利用了三维标签诱导的大斜窗匹配，又利用了神经网络预测的小正方形patch匹配，同时获得了与倾斜物体表面的一致性和像素相似度的鲁棒性。此外，我们的匹配成本分别在每个像素处进行计算。

2. Realted Work

三维标签的匹配成本计算不同于离散差异的匹配成本计算。每个像素点对应的不规则区域是由物体表面的切平面引起的，切平面随三维标签的不同而变化。在这种情况下，基于分段的方法综合了超级混合体内部的强度和梯度差异[9]，而基于补丁匹配的方法则在倾斜的补丁内部使用自适应权重进行聚合[1]。为了更好地处理曝光和光照变化，Zhang等人[11]和Yamaguchi等人[23]将像素之间的强度和梯度差异替换为小正方形面片之间的梯度和人口普查转换差异，但仅计算超级像素的匹配成本。Zbontar和LeCun[5]使用CNN来获得更好的方形面片匹配精度，仅在离散差异上使用前并行成本聚集。与上述方法不同的是，我们的双层匹配算法既利用了三维标签诱导的大斜窗匹配，又利用了神经网络预测的小正方形patch匹配，同时获得了与倾斜物体表面的一致性和像素相似度的鲁棒性。此外，我们的匹配成本分别在每个像素处进行计算。基于线段的方法自然地减少了三维标签的标签空间。一些作品使用过分割作为硬约束[24]，[25]，通过假设分段平面场景和鼓励相邻段对之间的平滑[23]，[26]。然而，它们存在分割不准确和非平面曲面的问题。以分割为软约束的方法较好地解决了这些问题。Bleyer等人。[13] 仅使用分割生成候选3D标签集，并从有限集优化最佳分配。Olsson等人[2]直接使用三维标签距离作为二阶平滑度的正则化项，并将分段平面建议与融合移动求解器融合。上述方法的缺点在于，只有包含在像素有限的候选标签集中，才能得到正确的3D标签。而我们只采用分割的方法在像素之间传播候选标签，而PatchMatch随机抽样策略保证了候选标签集的充分性。虽然我们还在像素级融合的建议更好的任务,我们的建议是精心设计的,这样他们可以融合α-expansions图,比融合更加高效和准确移动[20],特别是对高分辨率图像。

基于PatchMatch的方法也能有效地生成候选3D标签。作为一种局部方法[27]，原始的面片匹配立体模型不能很好地处理图像噪声和低纹理区域。应用不同的全局信息来解决这个问题。Heise等人[16]使用松弛变量迭代更新一元数据成本和全局变分平滑成本，但基于松弛变量的方法在极端非凸的情况下不能像预期的那样工作。Besse等人[15]将粒子信念传播的采样替换为相邻传播和随机采样，但是每个像素的3D标签的串行更新很容易陷入不需要的局部极小值。Taniai等人的[17]设计方案来自本地共享标签(LSL)，可以通过标准的图形切割来解决，这是与我们最相关的工作。缺点是使用相同大小的正方形共享区域会导致大量的冗余计算，并且大于共享区域的错误区域无法纠正。相反，我们引入分割结果来生成建议。在强度图像的指导下，我们的建议中的分段平面区域更可能与可能具有挑战性的像素区域对齐。此外，我们的多层结构能够同时处理复杂的表面和大的模糊区域。因此，我们的多层超混合方案的使用带来了更好的准确性和效率。

3.Proposed Method

A. Overview

该方法对每个像素的候选标签集进行迭代更新，优化候选标签集的最佳分配。候选标签集由提案{P i |i = 1,2，…， N}和优化是融合的建议。每个方案都是一个具有相同大小的输入图像的三通道图像。每个像素的三个值代表一个3D标签。该方法迭代更新每个像素的候选标签集，并优化候选集中的最佳分配。候选标签集由建议 { P i ∣ i = 1 , 2 ， … ， N } \{P^ i | i=1,2，…，N\} {Pi∣i=1,2，…，N}表示，并通过融合建议实现优化。每个方案都是一个三通道图像，与输入图像的大小相同。每个像素处的三个值表示一个三维标签。对于像素p，相应的候选3D标签集$L_p$由


我们设计一种新型superpixel结构有效更新的建议,这样可以进行融合α-expansion图。最后的三维标记显示了具有深度和表面法线的精确三维场景结构。图1给出了整个框架的工作流程。第三- b节至第三- e节将详细介绍这些步骤。

B. Formulation

它由两个数据项组成，一个是测量匹配像素之间的切面patch一致性，另一个是测量相邻像素之间的平滑性的两两正则化项。$N_p$包含像素p的四个相邻像素。

1)一元数据项:为了提高亚像素精度，我们将3D平面诱导的patch结构与CNN预测的像素相似性相结合，提出了一种新的$E_p(l_p)$双层数据代价。

如图2所示，为了缓解由大面片内部的深度变化引起的投影变形问题，对于来自参考图像的正方形面片，来自另一图像的相应面片的形状由由由3D标签表示的对象点的切面诱导。由于对应的patch的形状随着3D标签的不同而不同，因此patch的相似度测量比使用正方形patch更难加速。对于效率关注，现有的基于补丁匹配的方法通过像素强度和两个补丁之间的梯度差的加权和来建立数据成本，如果在左图像和右图像之间曝光或照度变化，则处理不良。

为了更强的鲁棒性和更好的准确性，近期的工作[5]，[28]使用CNN预测两个小图像块的相似性。可能的误差来源，包括图像噪声，光照变化，倾斜，和其他几何变形，可以通过训练的神经网络识别。然而，尽管增加补丁的大小可以减少匹配的模糊性，但是神经网络不能很好地处理大的补丁。一个原因是当patch的尺寸变大时，神经网络处理倾斜的能力仍然比使用带有3D标签的倾斜patch的能力差。

我们提出的双层数据成本利用了上述两种patch成本的优点，通过计算得到

对于原始面片匹配立体图，Zp的规格化是不必要的，因为它的值对于所有切面都保持不变。相反，在我们的例子中，数据项需要规范化以进行全局优化。

简单地说，我们的双层数据成本首先计算一维标签诱导的小正方形斑块的匹配成本，然后聚合在三维标签诱导的大斜斑块上。该神经网络设计用于用前并行图像块进行一维视差标记，能够矫正倾斜曲面的部分投影变形。因此，小块$R^L(q)和R^R(q)$的前沿并行假设误差仍然可以忽略。同时，$W_p$的大半径保证了与斜面的一致性。

2 )两两平滑项:我们相邻像素对上的平滑项有形式

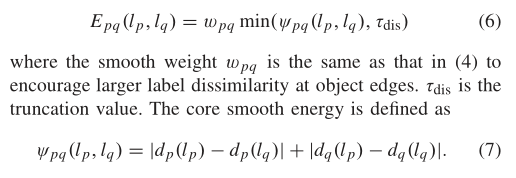
该函数在像素点p和q处测量两个3D平面在观察光线上的距离。较低的平滑能量倾向于视差和3D法线在相邻像素之间平滑变化。其主要优点是，作为一阶相互作用的成对函数，证明了二阶光滑性对视差[2]的增强作用。此外，这种能量在许多情况下鼓励高效的子模块融合[22]，这将在后面展示。

C. Superpixel Structure Construction

尽管在立体匹配中采用MRF模型是一种常见的方法，但由于每个节点的3D标签空间无限大，节点数目庞大，求解（2）的MRF仍然具有挑战性[15]、[17]、[19]。利用我们精心设计的超混合结构，我们的方法能够在较大的区域内有效地传播候选标记，并同时融合它们，因此有较高的机会跳出虚假的局部极小值，获得较低的收敛能量。

在观察到一个好的三维标注方案在大多数图像区域都是空间平滑的基础上，除了在对象边界处是不连续的之外，我们在超像素级生成建议。然而，如果直接根据分割结果构造分段平面方案，如[2]和[13]所述，则由于非亚模性质，无法通过α-展开有效地解决融合问题[22]。因此，我们提出了一种新的超混合提议结构。为了提高效率，我们预先构造了超级混合结构，从中可以方便地在每次迭代过程中更新超级混合方案。

我们的方法首先使用简单线性迭代聚类(SLIC)算法[29]对输入图像进行多次超像素分割M次。每个分割将输入图像分割成B个超像素。通过给B赋不同的值，分别得到由小超像素和大超像素组成的不同的分割，如图3所示。由于提案的3D标签会在每个超像素内设置几乎相同的值，较小的超像素会鼓励复杂表面的更多细节，而较大的超像素则提供了在相应区域跳出虚假局部极小值的可能性。因此，多层超像素分割比单个超像素分割具有更高的精度。

为了生成能够有效优化的方案，每个超级像素图像需要满足在四个相邻像素网格上每两个超级像素都是断开的。同时，像素优选包含在尽可能多的超级像素中。为了达到这一目的，我们在分割结果上采用了一种新的区域腐蚀方法。

对于每个分割结果，我们首先将超像素分成K组，这样来自同一组的任意两个超像素在4邻域像素网格上都不会相邻。根据四色定理[30]，K = 4的解总是存在的。在实际应用中，我们使用一个有效的贪心策略来得到计算复杂度问题的K = 5解。图3给出了一些真实图像的分组示例，其中K个不同的组用K种不同的颜色表示，类似于四色问题。图4(b)进一步显示了可能的小像素区域内的过程。

从每个分割的K个超像素组中，生成K个不同结构的超像素图像。对于第i个超像素图像，我们保持第i组的超像素不变，对所有其他超像素执行交叉核为5个像素的腐蚀操作。被侵蚀的像素被标记为“无效”。如图4©所示，除黄色组外的所有超像素均被侵蚀。

经过以上的处理步骤，我们提出的超像素结构包含了一些带有“无效”标记的K×M超像素图像。此外，在每个超像素图像中，任何两个相邻像素要么属于同一个超像素，要么包含至少一个“无效”标记。

D. Optimization

算法1总结了PMSC优化的全过程框架。根据第2行的特殊超级混合结构，我们的方法迭代地更新第5行和第6行的建议{P}={S}{C}，并在第8行通过α-展开将其融合。


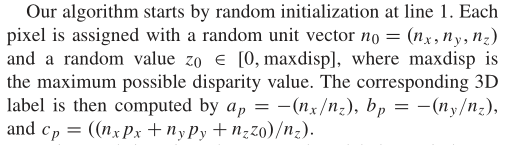
在每次迭代过程中，通过在第4行进行随机抽样，独立地提炼出当前最好的标签。首先将每个3D标签转换为视差和法向表示，然后迭代地将$[-{\Delta }_z^{max}，{\Delta }_z^{max}]$中的一个随机值添加到z0，将$[-{\Delta }_n^{max}，{\Delta }_n^{max}]$中的三个随机值添加到n0。

其中，$E_p(l)和E_{pq}(l_p,l_q)$与式(2)相同。对这里的能量项进行细化，试图以贪婪的方式找到所有其他像素标签为常数的最佳$l_p$。与此同时，我们的新型SC尝试同时更新超像素内的像素标签，从而比现有方法具有更高的精度。

由于我们精心设计的超像素结构，来自一个超像素提案的任何两个相邻像素要么具有相同的3D标签，要么包含至少一个“无效”标签。

在第6行，两个棋盘图建议C0, C1也通过从$l_{refine}$重新分组标签来更新，从而将改进的标签添加到候选标签集中。基于改进的最佳标识$l_{refine}$，这两个建议被更新

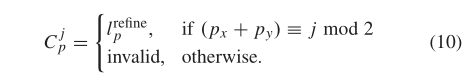
换句话说，$l_{refine}$中的像素是按照棋盘格方式划分的。一个方案包含所有黑色像素，而另一个方案包含所有白色像素。其余位置用“无效”标记填充。在这种情况下，这两个方案与superpixel融合方案具有相似的性质。图5示出了超级像素方案和棋盘格方案的更新过程。

所有的超像素建议和棋盘建议组成的建议集{P}。找到最好的融合结果从{P},我们迭代更新当前的最佳标签$l^{best}$通过执行α-expansion图切割的建议。[22]所示,α-expansion可以到达全球最低能量从两个建议只有在满足成对的两个建议

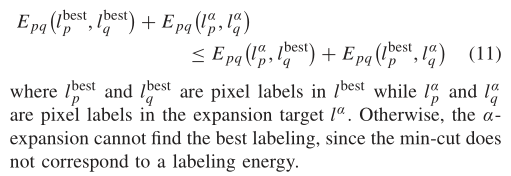
现有的一些方法直接使用简单的立体匹配方法的输出作为提案[2]、[13]。在他们的情况下,没有约束添加到四个标签$l_p^{best},l_q^{best},l_p^{\alpha },l_q^{\alpha }$,因此,经常(11)是违反了。因此，只有fusion move[20]可以应用于提案的融合。融合移动的缺点是计算复杂度高于α-扩展，在每个移动中只能达到部分融合结果而不是全局最小结果。

E. Implementation Details

对于全局PatchMatch方法，一个问题是计算复杂度高，这主要是由于每个像素的3D标签的自适应权值聚合的重复计算造成的。使用超像素提案的优点是边缘感知滤波器(EAFs)[31]、[32]可以很容易地降低计算复杂度。由于每个superpixel提案中的大多数像素都具有相同的3D标签，因此可以像在[19]和[33]中那样，通过过滤同时计算它们的数据成本，而不是对每个倾斜的窗口执行冗余计算。高效的EAF直接应用于我们的CPU实现超像素提案的数据成本计算。如果使用GPU加速，每个像素的patch的并行计算速度甚至比我们实验中使用EAFs的速度快10倍，因此EAF没有应用到我们的GPU实现中。

该方法可以很好地处理随机3D标签在第一行的初始化。为了更快的收敛速度，可以使用局部PatchMatch进行初始化。该方法首先利用局部有效的方法为每个像素单独找到一个好的三维标签，然后利用SC从好的初始值中找到全局最优的赋值项。一个障碍是局部PatchMatch计算复杂度高;因此，现有的实现根本没有效率。但是，在我们的示例中，我们使用可接受的运行时间以大规模并行的方式实现了局部PatchMatch，方法是用红黑顺序传播[34]代替局部PatchMatch的顺序传播。我们实现的局部PatchMatch初始化帮助PMSC在不受其他影响的情况下更快地收敛。

我们算法的流水线是为一个视图设计的。在计算左视图或右视图的视差图时，所有的分割和优化操作都仅在该视图上使用。结果表明，该算法对不一致分割具有很强的鲁棒性。为了得到最终的结果，我们分别在左视图和右视图上运行我们的算法；然后，使用自定义的左-右一致性检查来查找具有$|d_p^L–-d_{p^{\prime }}^R|>1$的不一致像素。这些像素用与较低视差相对应的左或右最近的一致3D标签重新填充。不进行其他后处理。

IV. EXPERIMENTS

A. Parameter Setting

在实验中，我们在Middle-bury 3.0基准[35]上对我们的方法进行了评估，该基准由30组高分辨率（高达3000×2000）图像和21组低分辨率（约450×350）图像组成的Middlebury 2006数据集[36]组成。首先，我们在米德尔伯里3.0的官方基准上根据不同的标准来评估我们的排名。接下来，我们测试每个模块的效果。然后，我们给出了与其他基于全局补丁匹配的方法的比较结果。最后分析了系统对参数和运行时间的敏感性。

我们的实验是在一台配备了i7-6700K 4.0-GHz CPU、40G内存和GTX TITAN X显卡的PC上进行的。为数据项,我们使用一个小窗口的11×11 CNN像素相似度计算和设置截断阈值τsim至0.5。CNN使用Middlebury 2001、2003、2005、2006和2014年的所有数据集[27]、[35]–[37]对图像进行训练，从每个图像对的每个11×11补丁中生成一个正样本和一个负样本。在可能的高分辨率图像的情况下，我们对倾斜的匹配窗口使用相对较大的值41×41。成本参数γ聚合权重设置为5。对于正则化项，将超像素层数M设置为4，期望的超像素数分别为200、1000、5000和25000。τ说截断差距不连续面设置为2。平衡数据项和正则化项,λ是设置为1。为了优化统一能量函数，我们进行了五次迭代。上述参数在我们所有的实验中都保持不变。

B. Evaluation on Middlebury Benchmark

我们的方法在Middlebury 3.0基准上进行了准确性评估。它有30个高分辨率的图像对，具有校正误差小、不同的曝光或左右图像之间不同的照度等条件。图像对分为15个图像对的训练集和测试集。划分的目的是防止过度的参数调优。隐藏测试集的Groundtruth视差图，只允许对算法结果进行一次评估。与此相反，提供了训练集的groundtruth视差图来帮助算法的开发。排序的总体错误率是15对图像错误率的加权平均值。为了公平比较，我们采用了半分辨率（高达1500×1000）的方法对基准进行评价，这与其他排名靠前的方法相同。

表1显示了我们的方法在测试集上不同标准下的平均误差，以及在默认标准“bad 2.0”下的其他前五种方法，包括MC-CNN[5]、MeshsteroE[11]、TMAP[38]、IDR[39] 和SGM[40]。“MC CNN acrt”是MC-CNN的准确版本，而“MC CNN fst”是快速版本。“Bad 0.5”、“Bad 1.0”、“Bad 2.0”和“Bad 4.0”是指在全分辨率下视差错误率分别大于0.5、1.0、2.0和4.0像素的缩写。“Avgerr”是指以像素为单位的平均绝对误差。“RMS”是指以像素为单位的均方根视差误差。“A50”、“A90”、“A95”和“A99”分别是以像素为单位的50%、90%、95%和99%误差分位数。我们的方法在所有十个标准中排名第一，优于所有其他公布的排名靠前的方法。由于输入图像是半分辨率的，因此“bad 2.0”和“bad 1.0”分别对应于Middlebury 2.0基准的“误差阈值1.0”和“误差阈值0.5”，这是比较立体匹配精度的常用标准。

我们还演示了与表II中设置的训练标准相同的顶级执行方法的等级。我们的方法在所有十项标准中仍然排名第一。结果表明，我们的方法在不同的挑战情况下，对所有30对图像都具有良好的鲁棒性。

图6分别示出了15个测试图像对上的最高执行方法的“坏2.0”错误率。我们列出了当前前三种方法的性能，并与广泛使用的SGM[40]进行了比较。我们的方法在15个测试图像对中的13个上达到了最低的错误率。图7示出了15个训练图像对上的相同错误率。我们的方法在15对训练图像中仍有10对达到了最低的错误率。


即使包含未发布的方法，我们的方法仍然是最精确的算法。表三显示了截至提交时米德尔伯里3.0基准的总体排名。在网页上，所提出的方法目前在七个标准下排名第一：“坏0.5”、“坏1.0”、“坏2.0”、“avgerr”、“rms”、“A50”和“A99”，在其他三个标准下排名第二或第三。

由于切平面法线和深度的联合正则化，我们的方法除了可以降低错误率外，还可以生成二阶平滑的视差图。为了实现二阶平滑度的可视化，我们在新视图下为每个由顶级执行方法生成的视差图绘制了一个三维网格。视差的微小误差会导致局部法线方向发生较大的变化，这一点在相应的三维网格中很容易观察到。图8显示了三种顶级方法和groundtruth的三对图像的结果。三维网格渲染没有纹理，以表达更多的细节在亚像素精度。即使MeshStereo也是基于3D标签的，但在MC-CNN和MeshStereo生成的网格中可以清楚地观察到光滑物体表面上的小凸起。与前两种方法相比，我们的方法生成的三维网格更自然、更准确，更接近于groundtruth。

图9显示了我们的方法的一些输出视差图，以及两个广泛使用的PatchMatch立体声方法[1]和SGM[40]。在具有挑战性的图像区域，我们的视差图在视觉上更加精确和自然，例如“Adiron”中的扶手、“Playrm”中的墙壁、“Playt”中的桌子和地板以及“Recyc”中的回收边界

C. Effectiveness of Each Module

为了验证分别作为数据项和作为正则项的多层SC的CNN相似度(PM CNN)的PatchMatch聚合的贡献，我们用不同的设置来测试我们的方法。完整的方法记为PM CNN +SC，表示两个模块都是活动的。对现有的基于补丁匹配的单元成本进行测试以进行比较。原始PatchMatch立体声的强度梯度数据成本无法处理数据集中的曝光或照明变化，因此产生更大的错误率（在某些图像对上超过70%），这里省略。相反，我们用广泛使用的梯度普查数据成本代替一元术语，用PM GC+SC表示。为了说明预训练相似度的优点，我们将底层斑块的CNN相似度替换为梯度统计量相似度，用PM-BLGC+SC表示，为了说明SC的有效性，我们通过设置λ=0分离SC的正则项，用PMCNN表示。为了比较现有的全局补丁匹配方法的最佳正则化项，我们还实现了[LS]中的LSL，它在基准米德尔伯里被关闭时在旧的2基准上的错误阈值0.5中排名第一，并且使用我们的PMCNN作为一元项，表示为PMCNN+LSL。表4列出了相应结果的错误率。在所有三个错误阈值下，PM-CNN+SC的错误率远低于PMCNN和PM-GC+SC，这表明PM-CNN和SC对高精度的贡献很大。此外，PM-CNN+SC也优于PM-BLGC+SC，说明CNN相似性在双层匹配成本上的优势。PM-BLGC+SC比PM-GC+SC更差的原因是前者放弃了部分矫正倾斜表面的能力。与PMCNN+LSL相比，PMCNN+SC仍具有较低的误码率，表明作为正则化项，我们的新SC优于现有的全局补丁匹配方法的最新正则化项。

另一个设置也被测试以显示分割精度的稳健性。如图10（b）所示，我们将SLIC超级混合直接替换为大小相似的正方形网格超级混合，这是不精确分割的极端情况。图10示出了作为示例的“Adiron”的不同设置的错误率。利用SLIC超混合进行优化，误差率最低，说明良好的分割有助于提高算法的精度。另一方面，直接使用网格超像素的精度并不差，说明我们的算法对分割误差具有很强的鲁棒性。“Mix”设置是两个视图分割不一致的一个例子，对应的错误率是在另外两个设置之间，说明我们的方法不太受分割不一致的影响。表四列出了在整个训练集上使用网格超像素的结果，用PM CNN + grid表示。总体错误率显示了相同的结论。由于在一个不准确的超像素内的像素不太可能像在一个完美的超像素内的像素那样共享类似的3D标签，所以沿着不准确的超像素传播的效率较低。同时，我们的能量函数不鼓励来自相同超像素的像素具有相同的3D标签;因此，我们的准确性不会因为不准确的定位而大大降低。此外，在计算一个视图的视差图时，所有的超像素层只在该视图上分段;因此，我们的方法是稳健的不一致分割。

D. Comparison With Other Global PatchMatch Methods

然后，我们将我们的方法与其他全局补丁匹配方法进行比较，包括PMBP[15]、SPM-BP[19]和GCLSL[17]。由于旧的Middlebury 2.0基准测试（由四个名为 “Tsukuba”、 “Venus”、 “Teddy”和“Cones”的图像对组成）几乎已经解决，因此它不再处于活动状态，并已升级到3.0版本，具备更具挑战性的条件。然而，大多数现有的全球补丁匹配方法是针对低分辨率图像设计的，大约为0.1像素。在新的基准上，对于超过1兆像素的高分辨率测试图像对，它们是难以处理的。例如，GCLSL[17]处理一个图像对需要2小时，而PMBP在合理设置下需要一天以上。因此，我们使用三分之一分辨率的Middlebury 2006数据集[36]进行彻底比较，该数据集由21个0.1兆像素的图像对组成，每个图像对之间没有曝光或照明变化。文中给出了PMBP[15]和SPM-BP[19]的具体实现。我们还实现了参数微调的GCLSL[17]。对于PMBP，我们按照建议设置粒子数K=5和迭代时间T=5。对于GCLSL，我们设置迭代时间T=10。PMBP、GCLSL和我们的方法的斑块大小都被设置为41×41，以便进行公平比较，而SPM-BP的参数则由作者调整。

表五显示了上述方法和我们的方法在21个测试图像对中的每一个上的错误率，错误阈值为一个像素。在非遮挡区域上评估错误率，这些区域是根据提供的左、右地面真值视差图计算的。我们的方法在21对图像中有17对达到了最佳的精度。值得注意的是，对于含有大的无纹理区域的图像对，在现有的全局补丁匹配方法不能很好地处理的情况下，我们的错误率远远低于次优。平均错误率是在最后一行计算出来的，而不像Middlebury 3.0 benchmark那样使用不同的权重；因此，平均错误率的排名取决于处理最具挑战性情况的能力。

前一种方法中的一些视差图的可视化如图11所示。误差差异用红色标记。我们在这里列出四组结果。前两行显示倾斜曲面的情况。尽管所有基于PatchMatch的方法处理倾斜曲面的效果相对较好，但我们的方法在极倾斜曲面上的效果更好，在曲面对象边界附近产生的误差分布更少。下面两行显示无纹理区域的情况。对于成对MRF模型，无纹理区域导致许多强大的局部极小值，现有的方法很难跳出。相比之下，我们的多层SC对伪局部极小值有更强的鲁棒性，同时CNN的像素匹配代价对噪声有更强的鲁棒性。因此，虽然理论上无纹理区域无法通过立体匹配得到完美的解决，但PMSC在无纹理区域上的性能要比其他全局补丁匹配方法好得多。

E. Parameter and Time Analysis

然后，我们评估了我们的方法对一些关键参数的敏感性。参数λ平衡的贡献一元数据成本和成对正则化成本。当λ设置为0,PMSC退化到一个本地方法,当λ设置为一个极大值,输出差异地图肯定是平滑。然而,PMSC是对λ的性能在一个相对较大的范围,如图12所示(一个)。我们列出了从Middlebury 3.0基准测试的训练集中随机选择的三对图像的错误率。所有三个图像的错误率对不同比例时,慢慢地从0.1到10λ。当λ> 10,由于oversmooth错误率增加迅速,而当λ< 0.1,由于不够正规化错误率增加缓慢。注意，x轴以对数坐标表示。窗口大小W控制近似切面的区域。窗口越大，曲面上的投影误差越大，而窗口越小，对模糊的鲁棒性越差。PMSC的性能在相对较大的范围内对W也不敏感，如图12（b）所示。

并对超混合层数M和超混合层数进行了详细的分析。图13示出了在两种图像对上具有不同M值和超级像素大小的性能。我们为不同的设置生成六个不同的分隔层供选择，每个分隔层有8、40、200、1000、5000和25000个预期的超级混合。使用0-6个最大超级混合层的错误率绘制为“M-Large”，而使用0-6个最小超级混合层的性能绘制为“M-Small”。图13（a）显示了包含足够纹理和复杂场景结构的“Motor”的错误率。图13(b)显示了“搁板”的错误率，其中包含大量未纹理但平面的区域。当M很小时，临界超像素大小与期望的场景结构有关。如图13(a)所示，使用三个最小的超像素层的错误率远低于使用三个最大的超像素层的“Motor”错误率。同时，图13（b）给出了“货架”的相反结论，原因是与较小的超级混合相比，使用较大的超级混合的传播能够同时改善较大的区域，但是在完美标记处采样的机会较低，因为长距离传播会增大3D标记误差。因此，小的超级混合层对于纹理化和复杂的场景是至关重要的，而大的超级混合层对于无纹理的平面是至关重要的。另一方面，毫无疑问，在这两种场景中使用更多具有不同超级像素大小的层可以获得更好或至少相似的精度，而由于附加的融合操作，运行时间几乎与M成线性增加。

不同迭代次数的性能如图14所示。图14（a）以“Adiron”图像对的总能量的变化为例，给出了不同超混合层M和不同迭代时间的情况。当M=0时，该方法退化为对每个像素独立的贪婪搜索，类似于SPM-BP和PMBP。优化被困在一个高能量的状态。当M从1增加到4时，加上更大的超混合，我们的方法能够跳出更具挑战性的局部最小状态，从而以更少的迭代次数在较低的能量下收敛。以“ArtL”图像对为例，分别使用和不使用局部PatchMatch初始化，其错误率如图14(b)所示。当优化从随机3D标签开始时，错误率从几乎100%缓慢下降，经过大约25次迭代后收敛。如果从局部PatchMatch初始化开始，优化将在几个迭代中收敛。注意，在这两种设置下，收敛的错误率是相同的。局部PatchMatch初始化步骤在没有其他影响的情况下加快了收敛速度。

就运行时间而言，我们的方法大约需要10分钟来生成高分辨率图像对（约1500×1000）的两个视图的最终视差图，其中高分辨率图像对从Middlebury 2014数据集中最多380个视差级别；低分辨率图像对（约450×350）从Middlebury 2006数据中最多85个视差层准备好了。相比之下，在处理 Middlebury2006年数据集的一对低分辨率图像时，SPM-BP大约需要40秒，而PMBP则需要17000秒。我们的方法是全局补丁匹配方法中速度最快的方法之一。

5.Conclusion

本文提出了一种基于三维标签的二阶平滑正则化立体精确匹配方法。我们提出了一个双层匹配代价，将CNN生成的像素相似值与PatchMatch立体声的倾斜patch匹配相结合，从而保持了两种测量方法的优点。为了生成每个像素的候选3D标签集，我们提出了一种基于多层超像素传播和随机细化的新策略。全局正则化定义为具有3D标签的像素网格MRF能量，由于我们设计了新颖的方案结构，可以直接通过α展开图切割进行优化。评估表明，所提出的方法获得高度准确的视差图，目前排名第一的官方米德尔伯里3基准之间的所有现有方法。与其他基于PatchMatch的全局匹配方法相比，该方法在Middlebury 2006数据集上取得了较好的效果，对高分辨率图像的处理效率更高。在未来，我们希望在PMSC模型中加入语义信息，并将我们的算法扩展到多视图场景。