1801. 积压订单中的订单总数；1567. 乘积为正数的最长子数组长度；923. 三数之和的多种可能

本文主要是介绍1801. 积压订单中的订单总数；1567. 乘积为正数的最长子数组长度；923. 三数之和的多种可能，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1801. 积压订单中的订单总数

核心思想：维护一个最小堆sell和一个最大堆buy，然后模拟即可。

1567. 乘积为正数的最长子数组长度

核心思想:动态规划，z表示以当前数字num结尾的乘积为正的最长子数组长度，f表示以当前数字num结尾的乘积为负的最长子数组长度。那么遇到正数num，正数个数肯定+1,不论前面有没有正数，负数个数，需要看前面有没有负数，有就+1；遇到负数num,那么就要看前面负数的个数，如果负数个数为0，那么正数长度为0,如果负数长度不为0,那么相乘为正，正数长度就+1，然后负数长度，不论前面有没有正数，都需要在正数长度上+1，按照我的定义出发看两遍代码就明白了。

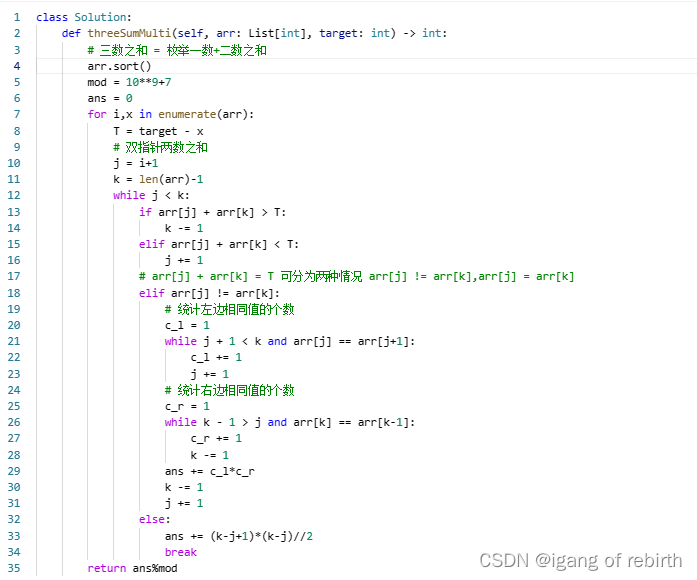
923. 三数之和的多种可能

核心思想：枚举+优化。如果直接枚举i,j,k，那么是O（n**3）超时了，所以我们就要进行优化，我们只用枚举i，然后把剩余的a[i+1:k]看作新的数组，那么就变成求两数之和的问题了，然后求两数之和，我们可以用双指针来做。这里是对arr排序过的，在没有重复数的双指针代码上改进一下就变成含有重复数字的了。