本文主要是介绍信号系统之滤波详解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1 过滤的基础
通常希望使用信号的幅度,而不是它的功率。例如,假设一个增益为20dB的放大器。根据定义,这意味着信号中的功率增加了 100 倍。由于幅度与功率的平方根成正比,因此输出幅度是输入幅度的 10 倍。虽然 20dB 意味着功率的 100 倍,但它仅意味着幅度的 10 倍。每 20 分贝意味着振幅变化了 10 倍。在等式形式中:

上述方程使用以 10 为底的对数;但是,许多计算机语言仅提供基本 E 对数的功能。可以通过修改上述公式来使用自然对数: d B = 4.342945 log ( P 2 / P 1 ) dB=4.342945\log(P_2/P_1) dB=4.342945log(P2/P1) 和 d B = 8.685890 log e ( A 2 / A 1 ) dB=8.685890\log e(A_2/A_1) dB=8.685890loge(A2/A1)。
图示:
分贝是表示两个信号之间比率的一种方式,因此非常适合描述系统的增益,即输出和输入信号之间的比率。然而,工程师也使用分贝来指定单个信号的幅度(或功率),方法是将其参考到某种标准。例如,术语:dBV 表示信号以 1 伏均方根信号为基准。同样,dBm 表示向 600 欧姆负载(约 0.78 伏均方根)产生 1 mW 的参考信号。
如果对分贝一无所知,请记住两件事:
- 首先,-3dB 表示振幅降低到 0.707(因此功率降低到 0.5)。
- 其次,记住分贝和振幅比之间的以下转换:

在自然发生的信号中表示信息只有两种常见方式。我们将这些称为:在时域中表示的信息,以及在频域中表示的信息。
在时域中表示的信息描述了某事发生的时间以及发生的幅度。例如,想象一个研究太阳光输出的实验。光输出每秒测量和记录一次。信号中的每个样本都表示该时刻正在发生的事情以及事件的级别。如果发生太阳耀斑,信号会直接提供有关其发生时间、持续时间、随时间推移的发展等信息。每个样本都包含无需参考任何其他样本即可解释的信息。
相比之下,在频域中表示的信息更间接。我们宇宙中的许多事物都表现出周期性运动。例如,用指甲敲击的酒杯会振动,发出铃声;恒星和行星绕着它们的轴旋转并相互旋转,依此类推。通过测量这种周期性运动的频率、相位和振幅,通常可以获得有关产生运动的系统的信息。假设对酒杯发出的声音进行采样。周期性振动的基频和谐波与材料的质量和弹性有关。单个样品本身不包含有关周期性运动的信息,因此也不包含有关酒杯的信息。该信息包含在信号中许多点之间的关系中。
这让我们想到了阶跃和频率响应的重要性。阶跃响应描述了系统如何修改时域中表示的信息。相反,频率响应显示了频域中表示的信息是如何变化的。这种区别在滤波器设计中绝对至关重要,因为不可能针对两种应用优化滤波器。时域性能良好会导致频域性能不佳,反之亦然。如果设计滤波器以消除心电图信号(在时域中表示的信息)中的噪声,则阶跃响应是重要参数,而频率响应则无关紧要。如果是为助听器设计一个数字滤波器(使用频域中的信息),则频率响应非常重要,而阶跃响应则无关紧要。现在,看看是什么使滤波器成为时域或频域应用的最佳选择。
3 时域参数
阶跃、脉冲和频率响应都包含相同的信息,只是排列方式不同。阶跃响应在时域分析中很有用,因为它与人类查看信号中包含的信息的方式相匹配。
例如,假设得到一个未知来源的信号,并分析它。要做的第一件事是将信号划分为具有相似特征的区域。有些区域可能是平滑的;其他可能具有较大的振幅峰值。这种分段是通过识别分隔区域的点来实现的。这就是阶跃函数的用武之地。阶跃函数是表示两个不同区域之间划分的最纯粹方式。它可以标记事件何时开始,或何时结束。它告诉你,左边的任何东西都与右边的东西有什么不同。这就是人类思维看待时域信息的方式:一组阶跃函数将信息划分为具有相似特征的区域。反过来,阶跃响应很重要,因为它描述了滤波器如何修改分界线。
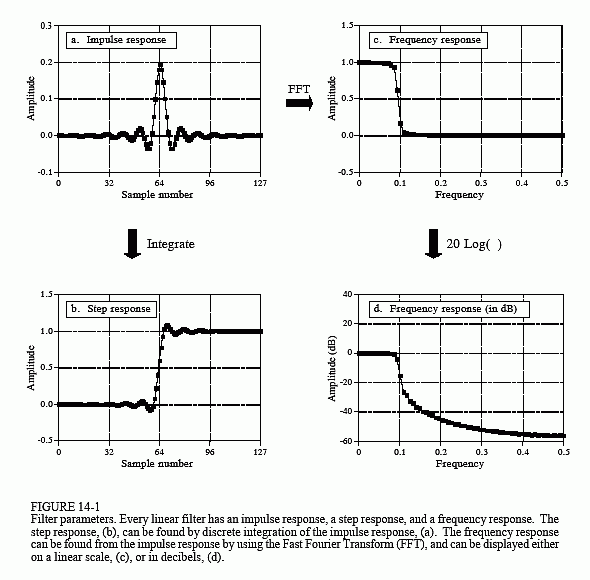
滤波器设计中重要的阶跃响应参数如图14-2所示。为了区分信号中的事件,阶跃响应的持续时间必须短于事件的间隔。这就决定了阶跃响应应尽可能快。如图所示,(a) 和 (b) 指定时间上升10% 和 90%。为什么不总是可以实现非常快的上升时间?原因有很多,降噪、数据采集系统的固有局限性、避免混叠等。
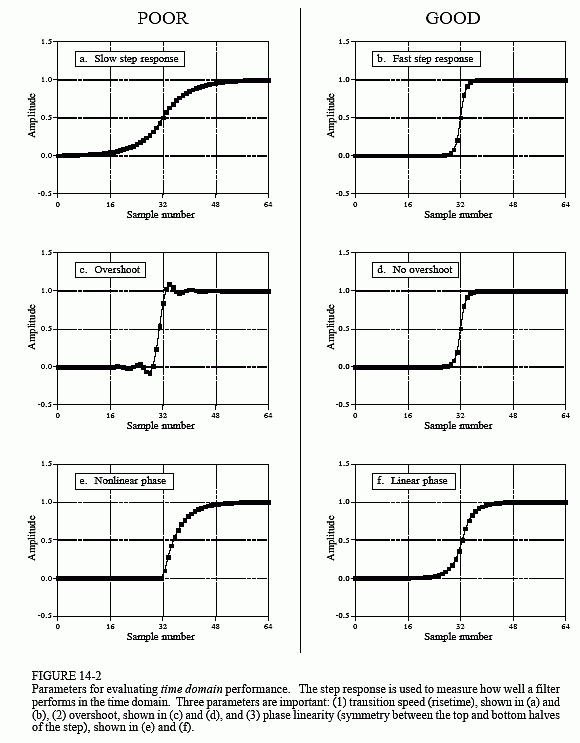
图(c)和(d)显示了下一个重要的参数:阶跃响应中的过冲(overshoot)。通常必须消除过冲,因为它会改变信号中样本的幅度;这是对时域中包含的信息的基本失真。这可以总结为一个问题:在信号中观察到的过冲是来自测量的物体,还是来自使用的滤波器?
最后,通常希望阶跃响应的上半部分与下半部分对称,如(e)和(f)所示。需要这种对称性才能使上升沿看起来与下降沿相同。这种对称性称为线性相位(linear phase),因为频率响应的相位是一条直线。
4 频域参数
图 14-3 显示了四种基本频率响应。这些滤波器的目的是允许某些频率原封不动地通过,同时完全阻挡其他频率。通带(passband)是指那些通过的频率,而阻带(stopband)包含那些被阻塞的频率。过渡带(transition band)介于两者之间。快速滚降(fast roll-off)意味着过渡带非常窄。通带和过渡带之间的划分称为截止频率(cutoff frequency)。在模拟滤波器设计中,截止频率通常定义为幅度降低到0.707(即-3dB)的位置。数字滤波器的标准化程度较低,通常将 99%、90%、70.7% 和 50% 的幅度电平定义为截止频率。
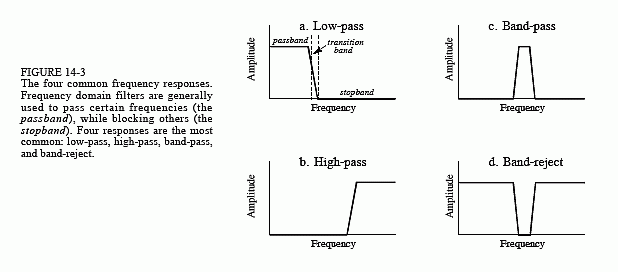
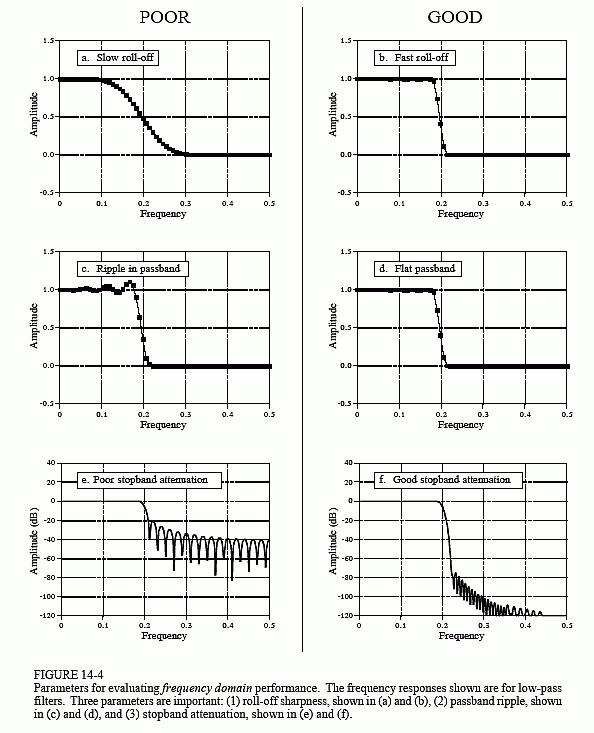
图 14-4 显示了测量滤波器在频域中性能的三个参数。为了分离间隔很近的频率,滤波器必须具有快速滚降,如(a)和(b)所示。为了使通带频率原封不动地通过滤波器,必须没有通带纹波,如(c)和(d)所示。最后,为了充分阻断阻带频率,必须具有良好的阻带衰减,如(e)和(f)所示。
为什么这些参数中没有关于相位的信息?首先,在大多数频域应用中,相位并不重要。例如,音频信号的相位几乎是完全随机的,并且包含很少的有用信息。其次,如果相位很重要,那么很容易使数字滤波器具有完美的相位响应,即所有频率都以零相移通过滤波器。相比之下,模拟滤波器在这方面是可怕的。
FFT 从滤波核 N 个样本开始,计算由 N 点实部和 N 点虚部组成的频谱。只有 FFT 实部和虚部的样本 0 到 N/2 包含有用的信息;其余点是重复的(负频率),可以忽略。由于实部和虚部对人类来说很难理解,因此它们通常被转换为极性符号。这提供了幅度和相位信号,每个信号从样本 0 到样本 N/2(即每个信号中的 N/2 + 1 个样本)。例如,256 个点的脉冲响应将导致从 0 点到 128 点的频率响应。样本 0 表示直流,即零频率。样本 128 表示采样率的一半。请记住,采样数据中不能出现高于采样率二分之一的频率。
用于表示脉冲响应的样本数可以任意大。例如,假设要查找由 80 个点组成的滤波器内核的频率响应。由于 FFT 仅适用于 2 的幂信号,因此需要在信号中添加 48 个零,以使其长度达到 128 个样本。这种用零填充不会改变脉冲响应。要理解为什么会这样,考虑当输入信号与系统的脉冲响应卷积时,这些添加的零会发生什么。添加的零只是在卷积中消失,并且不会影响结果。
更进一步,可以在脉冲响应中添加许多零,使其长度为256,512或1024点。重要的思想是,较长的脉冲响应导致频率响应中数据点的间隔更近。也就是说,有更多的样本分布在DC和采样率的一半之间。在极端情况下,如果脉冲响应中填充了无限个零,那么频率响应中的数据点就会无限小地靠近在一起,即一条连续的线。换句话说,滤波器的频率响应实际上是在直流和采样率的一半之间的连续信号。DFT的输出是这条连续线的采样。在计算滤波器的频率响应时,应该使用什么长度的脉冲响应?
记住,本问中讨论的“好”和“坏”参数只是概括。许多信号并没有整齐地归类。例如,考虑被 60 赫兹干扰污染的心电图信号。信息在时域中编码,但干扰最好在频域中处理。
5 高通、带通和带阻滤波器
高通滤波器、带通滤波器和带阻滤波器的设计方法是从低通滤波器开始,然后将其转换为所需的响应。因此,大多数关于滤波器设计的讨论只给出了低通滤波器的例子。低通到高通的转换有两种方法:光谱反演和光谱反转(spectral inversion and spectral reversal),两者都同样有用。
14-5 中显示了光谱反演的示例。图(a)显示了一个称为窗口sinc的低通滤波器内核。此筛选器内核的长度为 51 个点,尽管许多样本的值非常小,以至于它们在此图中显示为零。相应的频率响应如(b)所示,通过向滤波器内核添加13个零并获取64点FFT得到。要将低通滤波器内核更改为高通滤波器内核,必须执行两件事。
- 首先,更改过滤器内核中每个样本的符号。
- 其次,在对称中心的样本中添加一个。
这导致了高通滤波器内核如(c)所示,频率响应如(d)所示。频谱反演将频率响应从上到下翻转,将通带变为阻带,将阻带变为通带。换言之,它将滤波器从低通变为高通,从高通变为低通,从带通变为带阻,或将带阻变为带通。
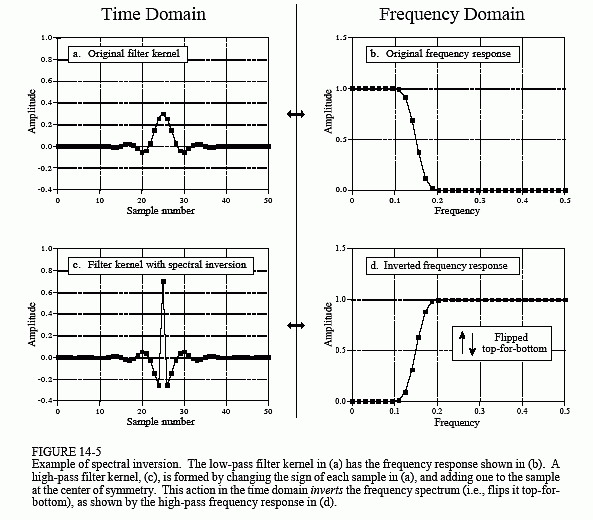
图 14-6 显示了为什么对时域进行两步修改会导致频谱反转。在(a)中,输入信号x[n]并联施加到两个系统。其中一个系统是低通滤波器,其脉冲响应由h[n]给出。另一个系统对信号不做任何操作,因此具有增量函数的脉冲响应,δ[n]。总输出 y[n] 等于全通系统的输出减去低通系统的输出。由于从原始信号中减去低频分量,因此输出中仅出现高频分量。因此,形成了一个高通滤波器。
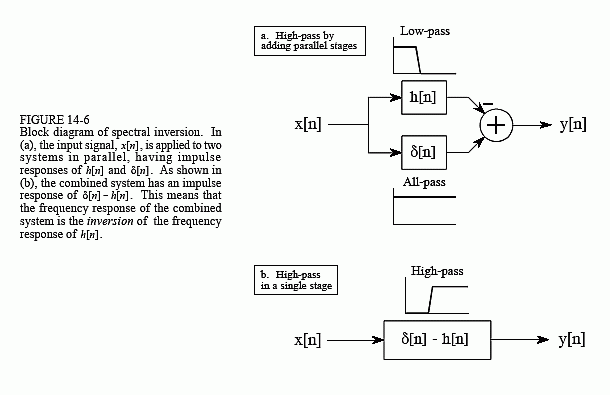
这可以作为计算机程序中的两步操作来执行:使信号通过低通滤波器,然后从原始信号中减去滤波后的信号。但是,通过组合两个滤波器内核,可以在信号级中执行整个操作。
通过增加脉冲响应,可以将具有附加输出的并联系统组合成一个级。如(b)所示,高通滤波器的滤波器内核由下式给出:δ[n]-h[n]。也就是说,更改所有样本的符号,然后在对称中心的样本中添加一个符号。
要使这种技术起作用,离开低通滤波器的低频分量必须与离开全通系统的低频分量具有相同的相位。否则,无法进行完全减法。这给该方法带来了两个限制:(1)原始滤波器内核必须具有左右对称性(即零相位或线性相位),以及(2)必须在对称中心添加脉冲。
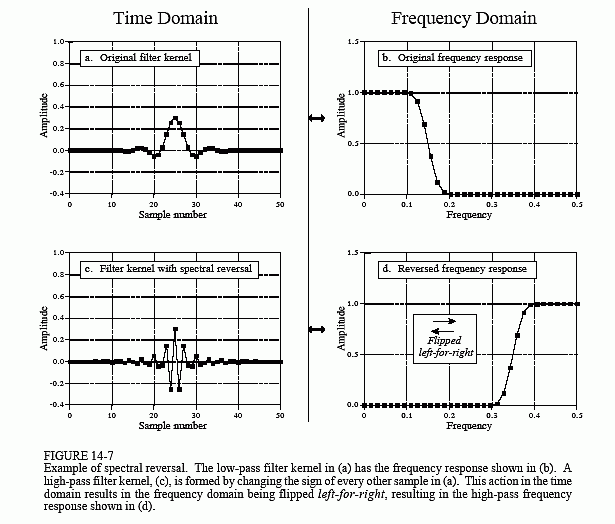
低通到高通转换的第二种方法,即频谱反转,如图14-7所示。和以前一样,(a)中的低通滤波器内核对应于(b)中的频率响应。高通滤波器核(c)是通过改变(a)中其他每个样本的符号而形成的。如(d)所示,这会将频域从左向右翻转:0变为0.5和0.5变为 0。示例低通滤波器的截止频率为0.15,因此高通滤波器的截止频率为0.35。
每隔一个样本改变一个符号,相当于将滤波核乘以频率为 0.5 的正弦曲线。这会产生频域移动 0.5 的效果。看看 (b) 并想象 -0.5 和 0 之间的负频率是 0 到 0.5 之间频率的镜像。(d)中出现的频率是从(b)偏移0.5的负频率。
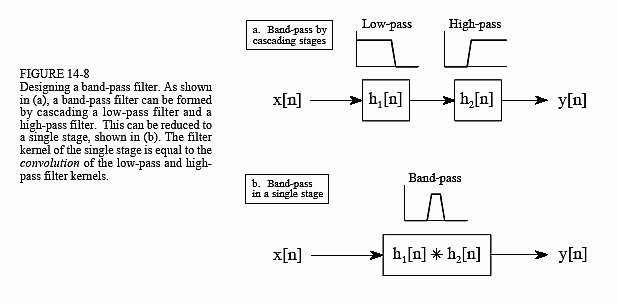
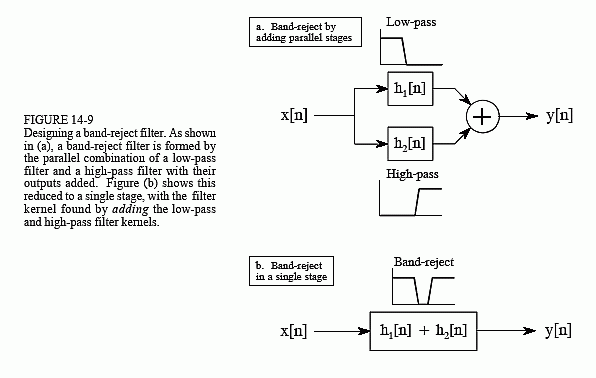
最后,图 14-8 和图 14-9 显示了如何组合低通和高通滤波器内核以形成带通和带阻滤波器。简言之,添加滤波器内核会产生带阻滤波器,而对滤波器内核进行卷积会产生带通滤波器。例如,可以通过添加两个滤波器内核来设计带通滤波器,以形成带通滤波器,然后如前所述使用光谱反演或光谱反转。
6 过滤器分类
表 14-1 总结了数字滤波器如何按其用途和实现进行分类。数字滤波器的使用可分为三类:时域、频域和自定义。如前所述,当信息以信号波形的形状进行编码时,使用时域滤波器。时域滤波用于以下操作:平滑、DC 去除、波形整形等。相反,频率过滤则应用在当信息包含正弦波分量的幅度、频率和相位时。这些滤波器的目标是将一个频带与另一个频带分开。
当滤波器需要特殊操作时,使用自定义滤波器,这比四种基本响应(高通、低通、带通和带阻)更复杂。
数字滤波器可以通过两种方式实现,即卷积(也称为有限脉冲响应或 FIR)和递归(也称为无限脉冲响应或 IIR)。通过卷积执行的滤波器比使用递归的滤波器具有更好的性能,但执行速度要慢得多。
这篇关于信号系统之滤波详解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







