本文主要是介绍通过seaborn对全球204个国家和地区进行定量分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
数据集为全球204个国家和地区的经济、外贸、寿命、疫情数据,主要以2021年数据为基准,部分缺失国家采用了2020年的数据。本文通过seaborn对世界数据进行定量和定性分析。

国际组织评定一个国家是否属于发达国家所考虑的指标除了该国的GDP规模之外,还会考虑其人均GDP/GNI、工业化水平、国民生活水平和它拥有的技术基础设施数量。除此之外,不过国际组织还会根据自身针对的领域特点,加入其他的考核因素。发达国家,又称已开发国家和先进国家。是指那些经济和社会发展水准较高,人民生活水准较高的国家,又称作高经济开发国家(MEDC)。发达国家的普遍特征是较高的人类发展指数、人均国民生产总值、工业化水准和生活品质。根据2021年的数据,目前获得全球正式承认的发达国家共有31个,这31个发达国家中,欧洲有23个国家、美洲有2个、澳洲有2个、亚洲有4个。
为划分世界各经济体收入水平,世界银行于 1978 年在世界发展报告中首次发布了国家收入分类标准以及人均国民总收入(GNI)指标的国家排序数据。世界银行国家收入分类标准,是国际社会分析研究世界各经济体经济社会发展状况、发展趋势、发展水平和发展差距的重要工具,也是世界各经济体开展全球合作治理、做出行政决策和制定发展战略的重要统计依据。世界银行按图表集法计算各经济体人均国民总收入(GNI),对世界各经济体经济发展水平进行分组。世界银行把全世界经济体划入四个收入组别:高收入、中等偏上收入、中等偏下收入以及低收入。通常,中、低收入国家被称为发展中国家,高收入国家被称为发达国家。
按照人均GNI,将它们分成四类,2021年的阈值是:
人均GNI在1085美元及以下是低收入经济体。
人均GNI在1086至4255美元是中等偏下收入经济体。
人均GNI在4256至13205美元是中等偏上收入经济体。
人均GNI在13205美元以上是高收入经济体。
第一部分为读取数据,查看数据为空和缺失情况
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import rcParams# ----------------------读取数据-----------------------
# 读取数据文件
dataset = pd.read_csv('世界经济人口数据.csv', encoding='utf-8')# 设置pandas显示的列数和浮点数格式
pd.set_option("display.max_columns", 33)
pd.set_option("display.float_format", "{:.5f}".format)# 查看数据,并输出前5条记录
print(dataset.head())
# 序号 国家/地区 洲 是否发达经济体 经济体收入类型 年份 GDP(美元) GDP占世界比重 \
# 0 1 美国 美洲 是 高收入经济体 2021 23315100000000.00000 0.24160
# 1 2 中国 亚洲 否 中等偏上收入经济体 2021 17734100000000.00000 0.18370
# 2 3 日本 亚洲 是 高收入经济体 2021 4940880000000.00000 0.05120
# 3 4 德国 欧洲 是 高收入经济体 2021 4259930000000.00000 0.04410
# 4 5 印度 亚洲 否 中等偏下收入经济体 2021 3176300000000.00000 0.03290# 查看数据类型和非空计数情况,以下仅为部分摘录数据
print(dataset.info())
# 部分字段为object类型,大部分指标为float64类型,序号和年份由于是数字的原因,也被认为是整数类型
# 有六个字段有空值情况
# # Column Non-Null Count Dtype
# --- ------ -------------- -----
# 0 序号 204 non-null int64
# 5 年份 204 non-null int64
# 6 GDP(美元) 204 non-null float64
# 7 GDP占世界比重 204 non-null float64
# 10 工业增加值(美元) 194 non-null float64
# 11 工业增加值占GDP比重 194 non-null float64
# 12 农林牧渔业增加值(美元) 194 non-null float64
# 13 农林牧渔业增加值占GDP比重 194 non-null float64
# 14 服务业增加值(美元) 194 non-null float64
# 15 服务业增加值占GDP比重 194 non-null float64第二部分为数据预处理,主要包括数据类型转换和数据缺失填充
# ----------------------数据预处理-----------------------
# ----------------------修改数据类型-----------------------
# 为避免序号和年份列参与计算,将序号和年份列设置为string类型
dataset["序号"] = dataset["序号"].astype("string")
dataset["年份"] = dataset["年份"].astype("string")# 再次查看一下数据类型,已变更为字符串类型
print(dataset.info())
# 0 序号 204 non-null string
# 5 年份 204 non-null string# ----------------------缺失值处理-----------------------
# 关于数据缺失情况,也可以用isna()查看,通过sum(),可以得到各列空值记录数
print(dataset.isna().sum())
# 工业增加值(美元) 10
# 工业增加值占GDP比重 10
# 农林牧渔业增加值(美元) 10
# 农林牧渔业增加值占GDP比重 10
# 服务业增加值(美元) 10
# 服务业增加值占GDP比重 10# 查看哪些行列存在缺失数据情况
print(dataset[dataset.isna().T.any()])
# 序号 国家/地区 洲 是否发达经济体 经济体收入类型 年份 GDP(美元) GDP占世界比重 \
# 145 146 新喀里多尼亚 大洋洲 否 中等偏上收入经济体 2021 10071351960.00000 0.00010
# 152 153 索马里 非洲 否 低收入经济体 2021 7628000011.00000 0.00010
# 154 155 关岛 大洋洲 否 中等偏上收入经济体 2021 6123000000.00000 0.00010
# 155 156 列支敦士登 欧洲 否 高收入经济体 2020 6113951011.00000 0.00010
# 156 157 法属波利尼西亚 大洋洲 否 高收入经济体 2021 6054676735.00000 0.00010
# 人均GDP GDP年度增长率 工业增加值(美元) 工业增加值占GDP比重 农林牧渔业增加值(美元) 农林牧渔业增加值占GDP比重 \
# 145 37159 0.02100 NaN NaN NaN NaN
# 152 446 0.04050 NaN NaN NaN NaN
# 154 35904 0.01060 NaN NaN NaN NaN
# 155 157754 -0.04980 NaN NaN NaN NaN
# 156 19914 0.01020 NaN NaN NaN NaN# 将对缺失列进行填充
# 因为前期对数据已经做了处理,数据质量还是挺高的,但这几个小国家的工农业增加值和占比,实在找不到相关数据
# 这些国家有两种分类方式,
# 一种是联合国的分类方式,即发达经济体和发展中经济体
# 一种是世界银行的分类方式:高收入、中等偏上收入、中等偏下收入以及低收入
# 基于同类型国家的经济模式大致是类似的判断,可以按照第二种标准进行数据缺失值填充
# 按经济体收入类型分组统计各指标的平均值
print(dataset.groupby("经济体收入类型").agg(['mean']))
# GDP(美元) GDP占世界比重 人均GDP GDP年度增长率 工业增加值(美元) \
# mean mean mean mean mean
# 经济体收入类型
# 中等偏上收入经济体 423777386707.42188 0.00439 14797.26562 0.06155 164856592593.98306
# 中等偏下收入经济体 164538363330.30188 0.00170 2584.90566 0.03528 49974011480.17308
# 低收入经济体 19149231901.72000 0.00020 694.56000 0.02198 4905145283.08333
# 高收入经济体 962921271208.74194 0.00998 44964.09677 0.04696 229544124425.28815
# 将相关缺失项的国家按照经济体类型的平均值进行缺失值天聪
dataset["工业增加值占GDP比重"] = dataset.groupby("经济体收入类型")["工业增加值占GDP比重"].transform(lambda x: x.fillna(x.mean()))
dataset["农林牧渔业增加值占GDP比重"] = dataset.groupby("经济体收入类型")["农林牧渔业增加值占GDP比重"].apply(lambda x: x.ffill().bfill())
dataset["服务业增加值占GDP比重"] = dataset.groupby("经济体收入类型")["服务业增加值占GDP比重"].apply(lambda x: x.ffill().bfill())
dataset['工业增加值(美元)'] = dataset['GDP(美元)'] * dataset['工业增加值占GDP比重']
dataset['农林牧渔业增加值(美元)'] = dataset['GDP(美元)'] * dataset['农林牧渔业增加值占GDP比重']
dataset['服务业增加值(美元)'] = dataset['GDP(美元)'] * dataset['服务业增加值占GDP比重']
# 再次查看哪些行列缺失数据,发现找不到了
print(dataset[dataset.isna().T.any()])第三部分为相关性分析
相关性是一种确定数据集中的两个变量是否以任何方式关联的方法。如何衡量相关性?
在数据科学中,我们可以使用r值,也称为Pearson的相关系数。这可测量两个数字序列(即列,列表,序列等)之间的相关程度。
r值是介于-1和1之间的数字。它告诉我们两列是正相关,不相关还是负相关。越接近1,则正相关越强。接近-1时,负相关性越强(即,列越“相反”)。越接近0,相关性越弱。
但是相关性强的列会造成共线性问题:
相关性高的特征放大了噪声的作用,多个特征实际平分了这类特征对模型的贡献,这就导致了模型对于数据的变动更加敏感,泛化误差增大;对于变量的分析造成影响,衡量变量的重要性贡献时候造成困难;越多的变量对于数据的处理计算压力越大。
首先看一下整体数据的相关性
# 输出数据相关性
print(dataset.corr())将数据拷贝到excel表中进行相关性分析,可以得到许多有趣和不为人知的结论。
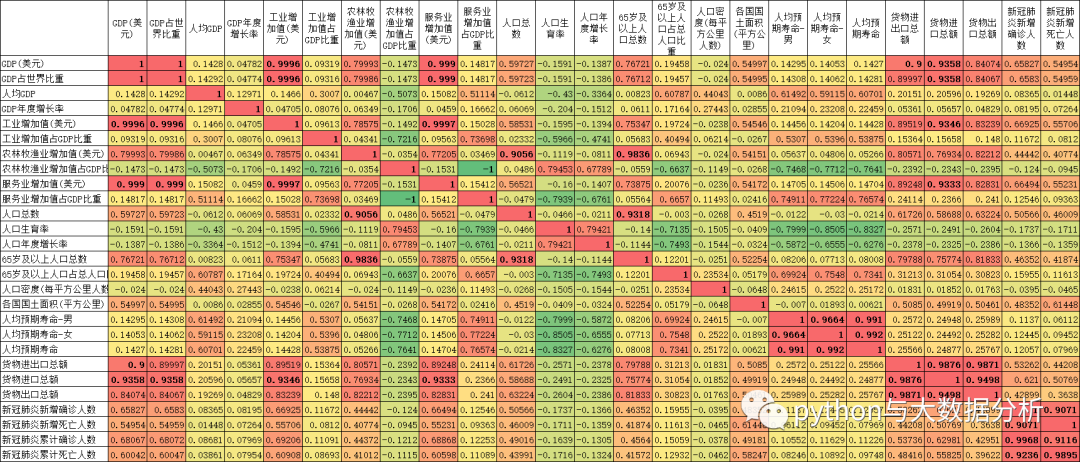
第四部分删除相关性较高的列
# 查看数据的相关性,并删除相关性较高的列
# 创建相关性矩阵
corr_matrix = dataset.corr().abs()
# 获取矩阵的上三角数据
upper = corr_matrix.where(np.triu(np.ones(corr_matrix.shape), k=1).astype(bool))
# 查找相关性系数>0.95的列
to_drop = [column for column in upper.columns if any(upper[column] > 0.95)]
# ['GDP占世界比重', '工业增加值(美元)', '服务业增加值(美元)', '服务业增加值占GDP比重',
# '65岁及以上人口总数', '人均预期寿命-女', '人均预期寿命', '货物进口总额',
# '货物出口总额', '新冠肺炎累计确诊人数', '新冠肺炎累计死亡人数']
# 删除相关列
dataset.drop(to_drop, axis=1, inplace=True)
print(dataset)
# 从26个指标项简化为16个指标项
# GDP(美元) 人均GDP GDP年度增长率 工业增加值占GDP比重
# 农林牧渔业增加值(美元) 农林牧渔业增加值占GDP比重 人口总数 人口生育率
# 人口年度增长率 65岁及以上人口占总人口比重 人口密度(每平方公里人数) 各国国土面积(平方公里)
# 人均预期寿命-男 货物进出口总额 新冠肺炎新增确诊人数 新冠肺炎新增死亡人数# 查看数据基本统计
print(dataset.describe())
# GDP(美元) GDP占世界比重 人均GDP GDP年度增长率 \
# count 204.00000 204.00000 204.00000 204.00000
# mean 470696743226.79413 0.00488 19064.52451 0.04544
# std 2127064905351.60278 0.02204 29457.11997 0.05957
# min 63100961.00000 0.00000 221.00000 -0.20740
# 25% 7940374102.75000 0.00010 2362.25000 0.01872
# 50% 28612804150.50000 0.00030 6930.00000 0.04235
# 75% 216967750000.00000 0.00222 23867.25000 0.06943
# max 23315100000000.00000 0.24160 234315.00000 0.31370第五部分,可视化分析
# ----------------------相关性分析-----------------------
corrmat = dataset.corr()
# 解决下面报错问题:TypeError: vars() argument must have __dict__ attribute
mpl.use('TkAgg')
plt.figure(figsize=(11, 7))
# 解决中文显示乱码,以下两种均可
rcParams['font.family'] = 'SimHei'
# sns.set(font='simhei')
# 解决刻度条负号为框
plt.rcParams['axes.unicode_minus'] = False
# 输出各指标的相关性系数和热力图
with plt.style.context({'axes.labelsize': 8, # 修改坐标轴标签字体大小'xtick.labelsize': 8,'ytick.labelsize': 8}): # 修改坐标轴刻度字体大小sns.heatmap(corrmat, xticklabels=corrmat.columns, yticklabels=corrmat.columns, center=0, cmap='RdYlGn_r',annot=True, annot_kws={'size': 8})
plt.tight_layout()
plt.show()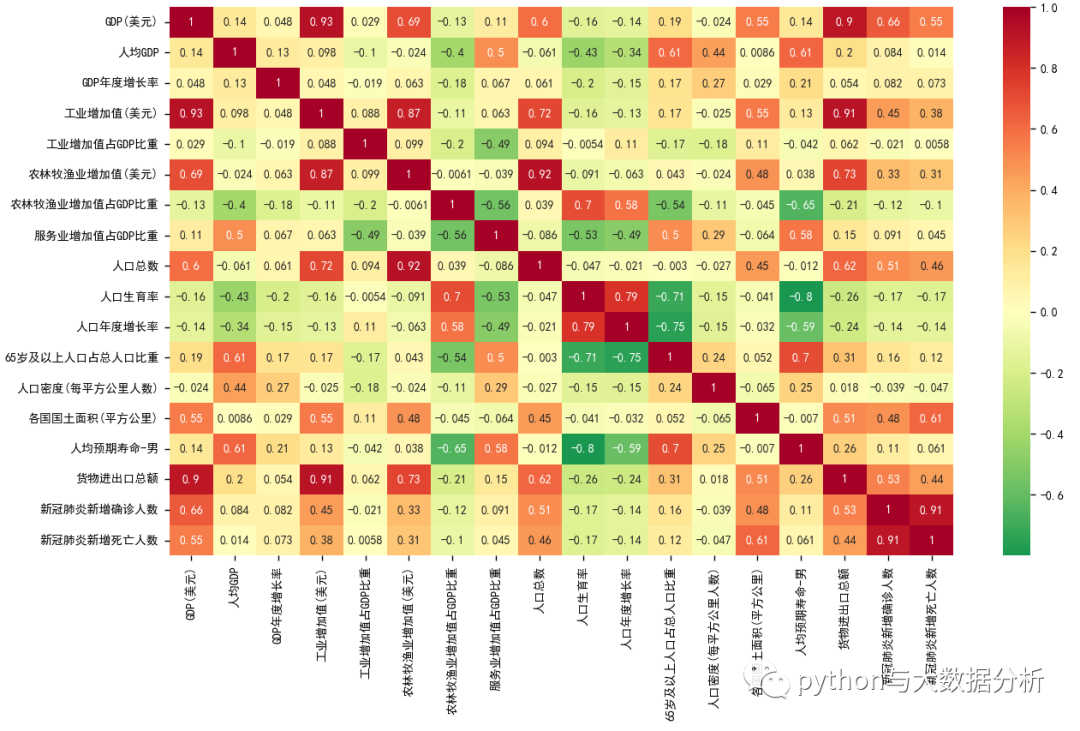
直接通过明细数据做定性分析
# 也可以直接通过明细数据做定性分析
# 通过sns.pairplot可以看到对角线上是各个属性的直方图(分布图),而非对角线上是两个不同属性之间的相关图
plt.figure(figsize=(14, 10))
sns.pairplot(dataset, kind="scatter", diag_kind='hist',plot_kws=dict(s=25, edgecolor="white", linewidth=2.5))
plt.tight_layout()
plt.show()
picfile='pic1.png'
plt.savefig(picfile)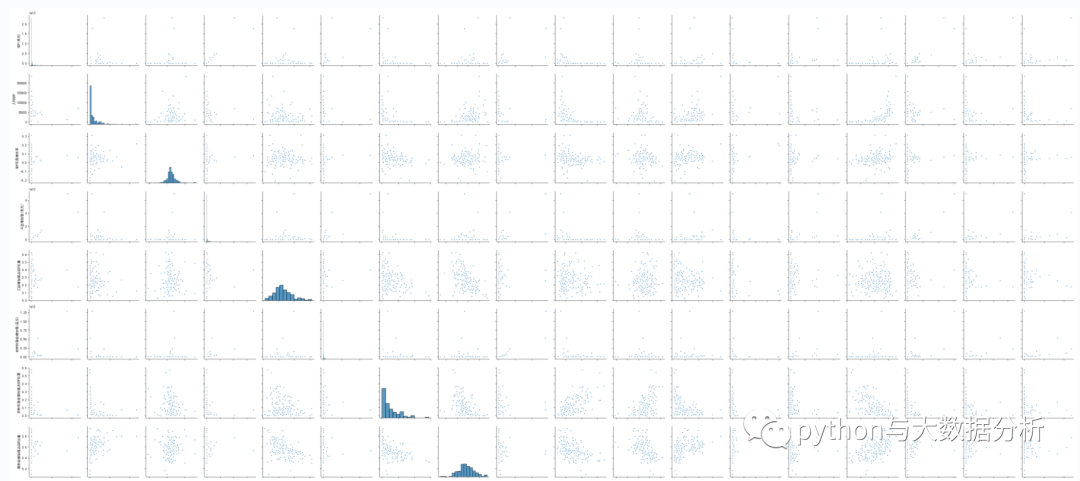
首先从直观上看:
1、GDP(美元) 、GDP占世界比重是一对100%强相关性指标
2、人均预期寿命-男、人均预期寿命-女、人均预期寿命是强相关性指标
3、货物进出口总额、货物进口总额、货物出口总额是强相关性指标
4、新冠肺炎新增确诊人数、新冠肺炎新增死亡人数、新冠肺炎累计确诊人数、新冠肺炎累计死亡人数是强相关性指标
其次,其他相关性较强的指标
工业增加值(美元)、服务业增加值(美元)、货物进口总额也是强相关性指标,毕竟工业和服务业越发达,GDP越高,货物出口也是刚刚的
人口总数、65岁及以上人口总数、农林牧渔业增加值(美元),也是强相关性指标,人数是靠农林牧副渔养的,也很正常
最后,异乎寻常的是
人均预期寿命-男、人均预期寿命-女、人均预期寿命和农林牧渔业增加值占GDP比重、人口生育率、65岁及以上人口占总人口比重成反比
可以说明的是,农林牧副渔比重越高就是农业和相对落后的国家,人口老龄化是不存在的,而且越是人均预期寿命越高,生育率越低。
新冠的相关指标和GDP关系不大,反而GDP越高,越不重视新冠疫情。
可以查看不同经济体与各组合指标的关系
# 还可以查看不同经济体与各组合指标的关系
plt.figure(figsize=(14, 10))
sns.pairplot(dataset, kind="scatter", diag_kind='hist', hue="是否发达经济体",plot_kws=dict(s=25, edgecolor="white", linewidth=2.5))
plt.tight_layout()
plt.show()
picfile='pic2.png'
plt.savefig(picfile)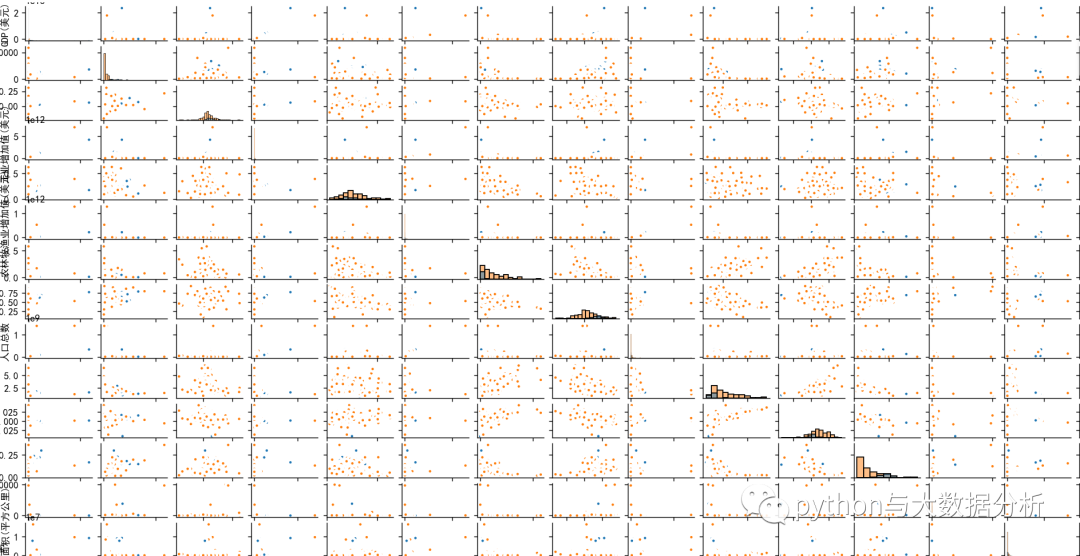
可以查看不同收入经济体与各组合指标的关系
# 还可以查看不同经济体与各组合指标的关系
plt.figure(figsize=(14, 10))
sns.pairplot(dataset, kind="scatter", diag_kind='hist', hue="经济体收入类型",plot_kws=dict(s=25, edgecolor="white", linewidth=2.5))
plt.tight_layout()
plt.show()
picfile='pic3.png'
plt.savefig(picfile)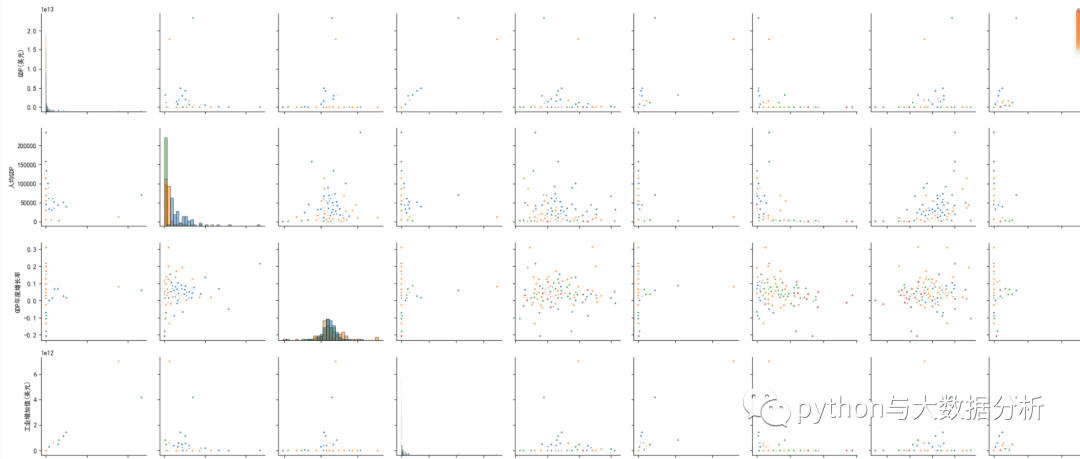
欢迎关注python与大数据分析

这篇关于通过seaborn对全球204个国家和地区进行定量分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







