本文主要是介绍笔试面试题目:盛水最多的容器,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
今天周末,来看G公司的一道面试题:
求max{|i-j|*min{a[i], a[j]}}的值,其中a是正整数数组,i和j的区间为[0, n-1].
这其实就是leetcode中的“盛水最多的容器”,如下:
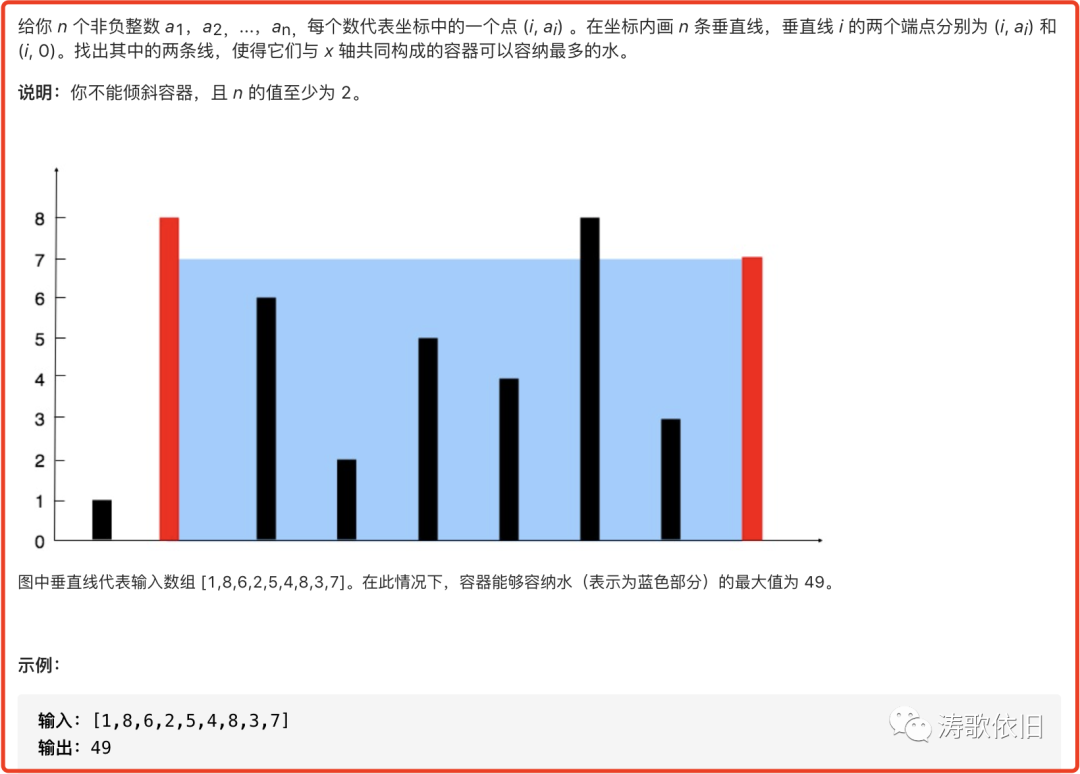
鲁迅说:暴力可以解决一切问题。
胡适说:暴力能解决的问题,都不是问题。
因为i和j的可能性是有限组合,所以暴力算法能得到结果,但无法通过面试。
用动态规划吗?貌似也不好动态规划。
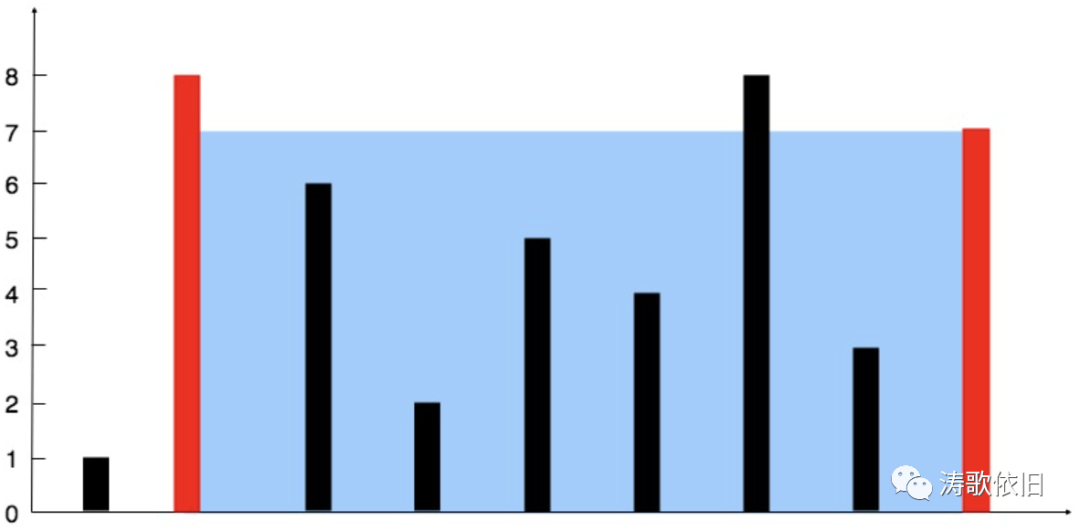
![]()
我们可以采用双指针,分别指向头尾,计算出盛水值。然后向中间搜索,尝试找出更大的盛水可能性。
木桶理论告诉我们:对于两块确定的盛水挡板而言,盛水的多少是由短板决定的。
所以,在向中间搜索时,从短板侧向中间移动指针,才有可能产生更大的盛水值。
这是一个核心结论。
至于代码,很简单,来看下:
func maxArea(a []int) int {n := len(a)if n < 2 {return 0}if n == 2 {return min(a[1], a[0])}max := min(a[n - 1], a[0]) * (n - 1)i := 0j := n - 1for i < j {if a[i] < a[j] {i++}else {j--}area := min(a[i], a[j]) * (j - i)if area > max {max = area}}return max
}func min(x, y int) int {if x < y {return x}return y
}结果:
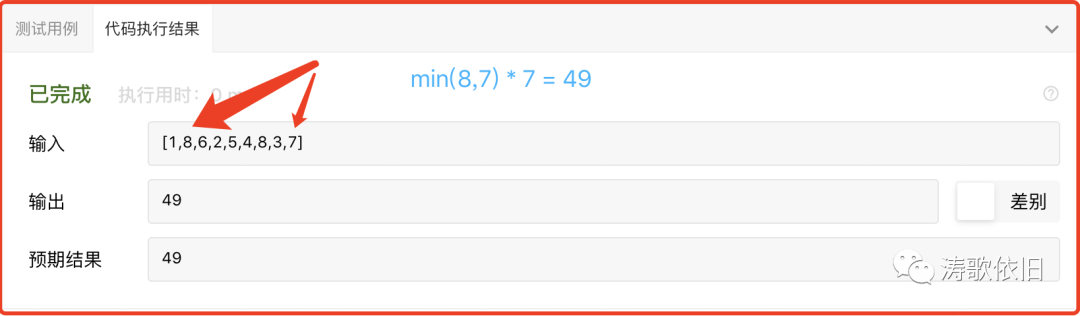
该算法能正常通过面试,祝大家获得自己心仪的offer.
周末愉快。
这篇关于笔试面试题目:盛水最多的容器的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





