集训总结（年前）

本文主要是介绍集训总结（年前），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

$1.29$ ~ $2.4$ 集训总结

集训学了数据结构优化DP、动态开点线段树、可持久化线段树、图论。

打了四场比赛，每场比赛都有 $8$ 题，时间 $3$ 小时 $15$ 分钟。

题目

$1.$ 踢踏舞

题面

小 C 和小 T 最近在学习踢踏舞。这种舞蹈大部分由用特制舞鞋击打地板的动作组成。小 C 和小 T 学得很快，他们甚至开始自己编排舞曲。

踢踏舞的编舞可以用一串包含两种字母 L和 R的序列来表示。

L表示用左脚击打地板，R表示用右脚击打地板。小 C 意识到踢踏舞中最精彩的部分就是舞蹈中两只脚互相交替击打地板的部分，即在这部分中，没有连续的两次动作是用同一只脚击打地板的。他定义一种踢踏舞编舞的价值为序列中最长的一段连续子序列，其中不包含连续的两个L或 R。

我们都知道，编舞的工作非常有挑战性，需要做出很多的调整，直到完成编舞。对于每次小 T 的调整，小 C 想要知道目前这种编舞的价值。小T的一次调整即为将序列中的 L改为 R，反之亦然。 在小T开始调整之前，整段序列只由 L组成。

输入格式及范围

第一行包括两个正整数，编舞序列的长度 $N$ ($1⩽N⩽200000$)，以及小Ｔ调整的次数 $Q$( $1⩽Q⩽200000$).

接下来有 $Q$ 行，每行包括一个数字 $x$ 表示小Ｔ调整的动作在序列中的位置。

输出格式

输出包括 $Q$ 行，每行数字表示小Ｔ每次调整之后编舞序列的价值。

样例1

输入
6 2
2
4
输出
3 5

样例2

输入
6 5
4
1
1
2
6
输出
3
3
3
5
6

解法

此题很容易想出，正解的复杂度是 $\Theta (N\log N)$ 的。

此题通过题目可知不能离线。

又有 $N$ 次修改查询，所以只能用每一次 $\Theta (N\log N)$ 的算法。

我们可以想到分治。

分治可以有三种情况：

1. 答案区间都在中间点左边

2. 答案区间都在中间点右边

3. 答案区间跨越中间点

如下图：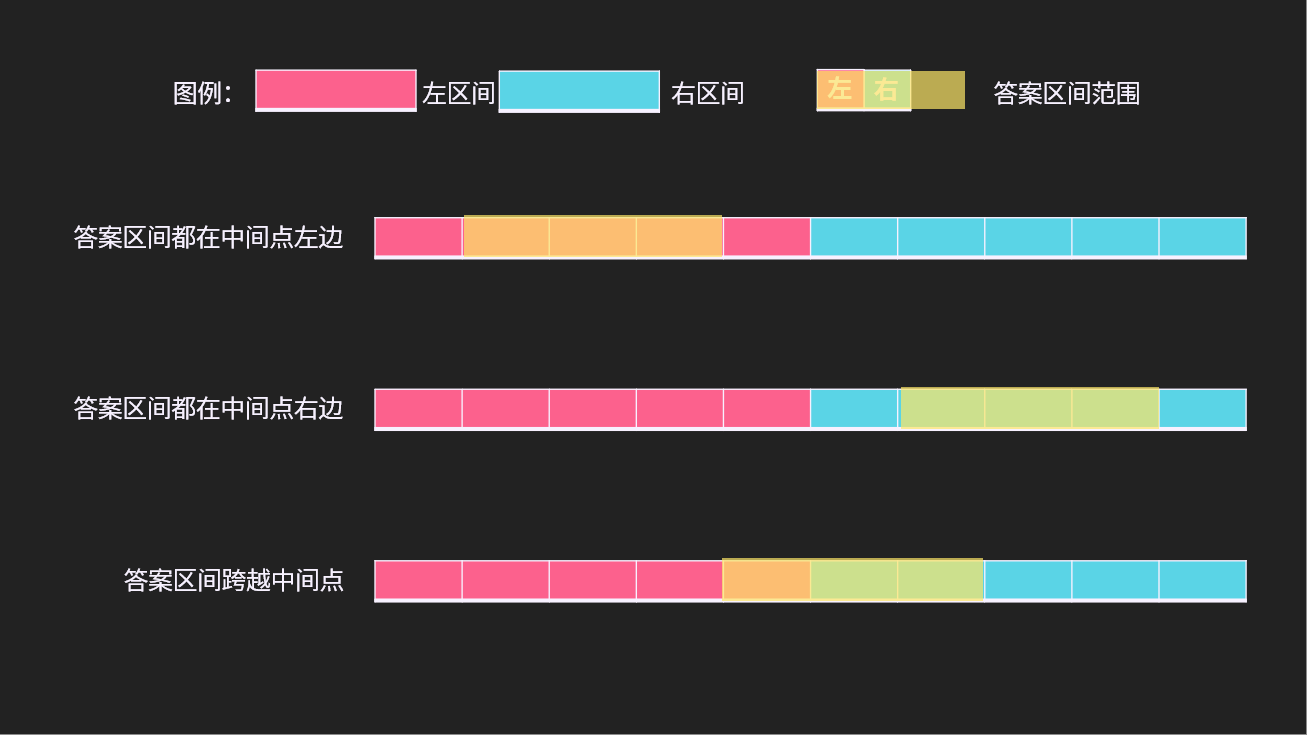

对于前 $2$ 种情况，可以直接递归下去。

对于第 $3$ 种情况，我们可以拆成两个区间，如图。

又由于是区间操作，所以可以使用线段树。

线段树可以保存 $3$ 个值：答案、紧贴左边的、紧贴右边的。

计算的代码如下：

void Update(Node &This, Node LChild, Node RChild) {This.LAns = LChild.LAns;This.RAns = RChild.RAns;This.Ans = std::max(LChild.Ans, RChild.Ans);if (Dance[LChild.R] != Dance[RChild.L]) {This.Ans = std::max(This.Ans, LChild.RAns + RChild.LAns);if (LChild.LAns == LChild.R - LChild.L + 1) {This.LAns += RChild.LAns;}if (RChild.LAns == RChild.R - RChild.L + 1) {This.RAns += LChild.RAns;}}}

其它就是一棵单点修改区间查询的线段树了，以下是代码：

#include <algorithm>
#include <iostream>
#include <string>std::string Dance;
int N, Q;class SegmentTree {
private:struct Node {int L, R, Ans, LAns, RAns;} SegmentTreeArr[800005];void Update(Node &This, Node LChild, Node RChild) {This.LAns = LChild.LAns;This.RAns = RChild.RAns;This.Ans = std::max(LChild.Ans, RChild.Ans);if (Dance[LChild.R] != Dance[RChild.L]) {This.Ans = std::max(This.Ans, LChild.RAns + RChild.LAns);if (LChild.LAns == LChild.R - LChild.L + 1) {This.LAns += RChild.LAns;}if (RChild.LAns == RChild.R - RChild.L + 1) {This.RAns += LChild.RAns;}}}public:void Build(int NodeId = 1, int L = 1, int R = N) {SegmentTreeArr[NodeId] = {L, R, 1, 1, 1};if (L == R) return;int M = (L + R) / 2;Build(NodeId * 2, L, M);Build(NodeId * 2 + 1, M + 1, R);}void Edit(int Position, int NodeId = 1) {if (SegmentTreeArr[NodeId].L == SegmentTreeArr[NodeId].R) {if (Dance[Position] == 'L') Dance[Position] = 'R';else Dance[Position] = 'L';return;}int M = (SegmentTreeArr[NodeId].L + SegmentTreeArr[NodeId].R) / 2;if (Position <= M) {Edit(Position, NodeId * 2);} else {Edit(Position, NodeId * 2 + 1);}Update(SegmentTreeArr[NodeId], SegmentTreeArr[NodeId * 2], SegmentTreeArr[NodeId * 2 + 1]);}int Query(int L, int R, int NodeId = 1) {if (L <= SegmentTreeArr[NodeId].L && SegmentTreeArr[NodeId].R <= R) return SegmentTreeArr[NodeId].Ans;if (L > SegmentTreeArr[NodeId].R || R < SegmentTreeArr[NodeId].L) return 0;int M = (SegmentTreeArr[NodeId].L + SegmentTreeArr[NodeId].R) / 2;return Query(L, M, NodeId * 2) + Query(M + 1, R, NodeId * 2 + 1);}
} C1888_P5;int main() {std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);std::cin >> N >> Q;for (int i = 0; i <= N; i++) {Dance += 'L';}C1888_P5.Build();for (int i = 1; i <= Q; i++) {int Pos;std::cin >> Pos;C1888_P5.Edit(Pos);std::cout << C1888_P5.Query(1, N) << '\n';}return 0;
}

理解

线段树不仅仅能求区间和，还可以求一些分治的问题。

$2.$ 求负环、毕加猪

求负环很简单，大家都知道。
代码：

#include <cstring>
#include <iostream>using namespace std;
int Vertex, Edge;
struct EdgeNode {int VertexStart, VertexEnd, Weight;
};
EdgeNode Edges[10005];
int Dis[1005];
#define ERR_NegativeRing (-0x114514)
#define ERR_NoPath (-0x1919810)
#define NoPath 0x3F3F3F3Fint BellmanFord(int Start, int End) {memset(Dis, 0x3F, sizeof(Dis));Dis[Start] = 0;bool Update;for (int i = 1; i <= Vertex + 1; i++) {Update = false;for (int j = 1; j <= Edge; j++) {int CurrentStart, CurrentEnd, CurrentWeight;CurrentStart = Edges[j].VertexStart;CurrentEnd = Edges[j].VertexEnd;CurrentWeight = Edges[j].Weight;if (Dis[CurrentStart] + CurrentWeight < Dis[CurrentEnd]) {Dis[CurrentEnd] = Dis[CurrentStart] + CurrentWeight;Update = true;}}if (!Update)break;i++;}if (Dis[End] == NoPath)return ERR_NoPath;else if (Update)return ERR_NegativeRing;elsereturn Dis[End];
}int main() {cin >> Vertex >> Edge;for (int i = 1; i <= Edge; i++) {cin >> Edges[i].VertexStart >> Edges[i].VertexEnd >> Edges[i].Weight;}int Ans = BellmanFord(1, Vertex);if (Ans == ERR_NegativeRing) {cout << "YES\n";} else {cout << "NO\n";}return 0;
}

正题：毕加猪

题面

圣诞节那天，大家聚在一起开 party 庆祝。猪丽叶和嫦娥在聊天，

当她们聊到毕加猪的时候，她们发现小猪竟然对她们都表白过。

她们很生气，决定一起整整小猪（花心的小猪完蛋咯！！）。

她们都去约小猪，要小猪在明天的 $A$ 时刻到她们家，不然就不理小猪。

小猪不想失去她们任何一个，但是他又不能在同一时间出现在两个不同的地方。

小猪突然想起来，猴哥的月光宝盒可以穿越时空，于是他向猴哥借来了月光宝盒，

但是它只能在指定的位置使用。有了月光宝盒，小猪可以先到其中一个MM家，待 $T$ 分钟之后，再借助月光宝盒，穿越时空，让他能在 $A$ 时刻出现在另一个MM家。

（故事背景无不良引导，不要关注）

输入格式

第一行一个整数 $cas$，表示每一个测试点有 $cas$ 组数据。

每组测试数据第一行包含三个整数 $N$，$M$，和 $T$，表示 $N$ 个点，$M$ 条边和小猪需要在MM家待的时间。

接下来行，每行三个整数 $a$，$b$，$c$ 表示有一条边从 $a$ 到 $b$ 要花 $c$ 时间，

如果 $c$ 为负表示可以在 $a$ 点使用月光宝盒，到达点，回到 $|c|$ 时间以前。

最后一行两个整数 $p$ 和 $q$，表示猪丽叶家和嫦娥家的编号。

输出格式

对于每组测试数据，输出 yes或者 no，表示小猪能不能同时满足两个MM的要求。能的话输出 yes否则输出 no。

样例1

输入
1
3 2 1
1 2 3
2 3 5
1 3
输出
no

样例2

输入
2
3 2 1
1 2 3
2 3 -5 
1 3
3 2 1
1 2 3
2 3 -3
1 3
输出
yes
no

数据范围

对于 $30\%$ 的数据：$N⩽20$，$M⩽100$，$cas⩽10$，$|c|⩽1000$。

对于 $60\%$ 的数据：$N⩽100$，$M⩽1000$，$cas⩽10$，$|c|⩽1000000$。

对于 $90\%$ 的数据：$N⩽200$，$M⩽3000$，$cas⩽10$，$|c|⩽1000000$。

对于 $100\%$ 的数据：$N⩽1000$，$M⩽10000$，$cas⩽10$，$|c|⩽1000000$。

解法

不必使用 SPFA，因为SPFA已死$\Theta (N\times M)$足够用了。

此题本质上就是一个求负环，但是求负环的时候要求出到底能不能到达终点，判断是不是“死环”（如下图）。

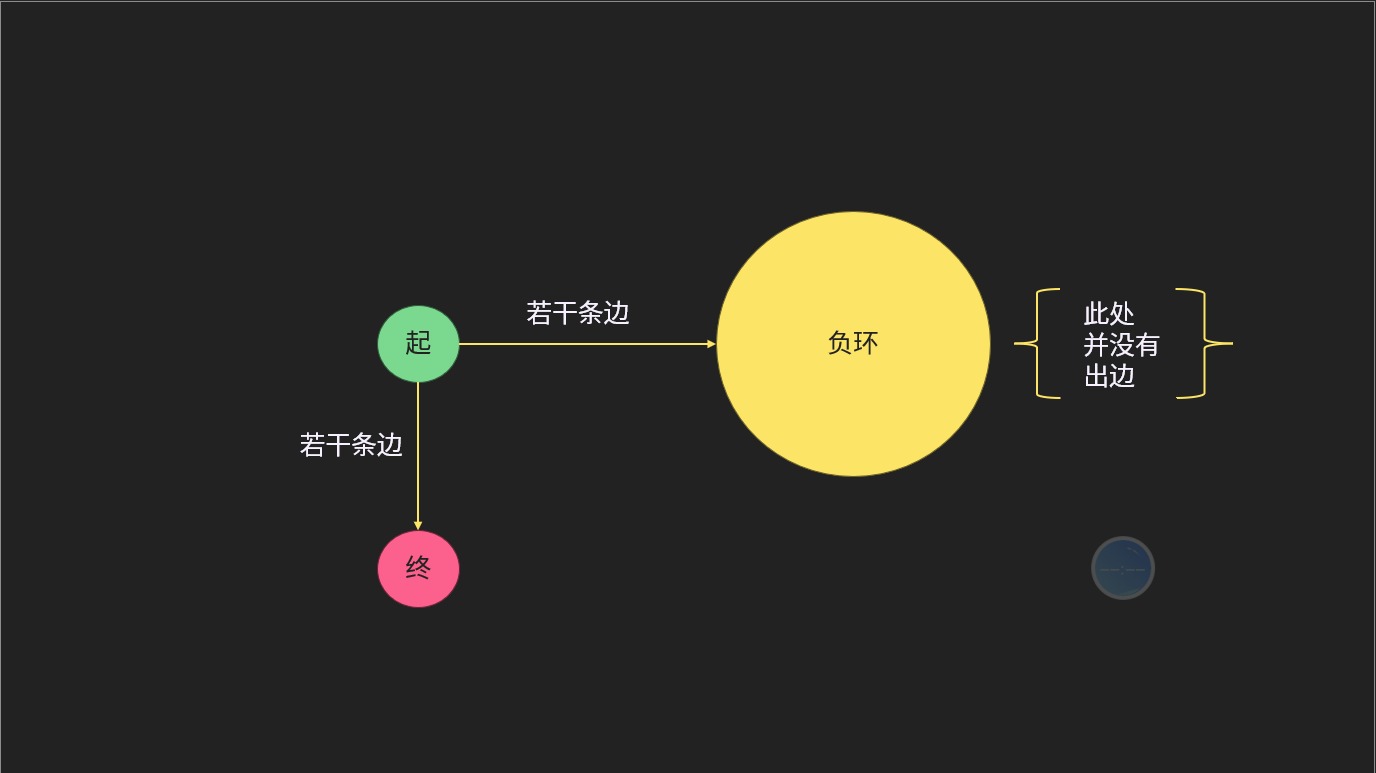
而且也并不是只能因为负环而输出 Yes，而且可以通过“负路径”也可以输出 Yes。

代码

#include <cstring>
#include <iostream>
#include <vector>using namespace std;
int Vertex, Edge;
struct EdgeNode {int VertexStart, VertexEnd, Weight;
};
EdgeNode Edges[10005];
int Dis[1005], Vis[1005];
int Update2;
std::vector<int> Graph[1005];
#define ERR_NegativeRing (-0x114514)
#define ERR_NoPath (-0x1919810)
#define NoPath 0x3F3F3F3Fbool Finish(int Node1, int End) {if (Node1 == End) return true;Vis[Node1] = Update2;for (int Node2: Graph[Node1]) {if (Vis[Node2] != Update2 && Finish(Node2, End)) return true;}return false;
}int Time, Pig1, Pig2;bool BellmanFord(int Start, int End) {memset(Dis, 0x3F, sizeof(Dis));Dis[Start] = Time;bool Update;for (int i = 1; i < Vertex; i++) {Update = false;for (int j = 1; j <= Edge; j++) {int CurrentStart, CurrentEnd, CurrentWeight;CurrentStart = Edges[j].VertexStart;CurrentEnd = Edges[j].VertexEnd;CurrentWeight = Edges[j].Weight;if (Dis[CurrentStart] + CurrentWeight < Dis[CurrentEnd]) {Dis[CurrentEnd] = Dis[CurrentStart] + CurrentWeight;Update = true;}}if (!Update) break;}if (Dis[End] <= 0) return true;for (int j = 1; j <= Edge; j++) {int CurrentStart, CurrentEnd, CurrentWeight;CurrentStart = Edges[j].VertexStart;CurrentEnd = Edges[j].VertexEnd;CurrentWeight = Edges[j].Weight;if (Dis[CurrentStart] + CurrentWeight < Dis[CurrentEnd]) {//Dis[CurrentEnd] = Dis[CurrentStart] + CurrentWeight;Update2++;if (Finish(CurrentStart, End)) return true;}}return false;
}int main() {int T;std::cin >> T;for (int t = 1; t <= T; t++) {cin >> Vertex >> Edge >> Time;for (int i = 1; i <= Vertex; i++) Graph[i].clear();for (int i = 1; i <= Edge; i++) {cin >> Edges[i].VertexStart >> Edges[i].VertexEnd >> Edges[i].Weight;Graph[Edges[i].VertexStart].push_back(Edges[i].VertexEnd);}std::cin >> Pig1 >> Pig2;if (BellmanFord(Pig1, Pig2) || BellmanFord(Pig2, Pig1)) std::cout << "yes\n";else std::cout << "no\n";}return 0;
}

$3.$ 数列 max 更新

题面

DCrusher 有一个数列，初始值均为 $0$，他进行 $N$ 次操作，每次将数列 $[a,b)$ 这个区间中所有比 $k$ 小的数改为 $k$。

他想知道 $N$ 次操作后数列中所有元素的和。他还要玩其他游戏，所以这个问题留给你解决。

输入格式

第一行一个整数 $N$，然后有 $N$ 行，每行三个正整数 $a,b,k$。

输出格式

一个数，数列中所有元素的和

样例

输入
4
2 5 1
9 10 4
6 8 2
4 6 3
输出
16

数据范围

$N⩽400,a,b,k⩽10^9$

解法

本题是主席树较板子题（可以离散化）。
区间修改区间查询。

代码

#include <iostream>typedef long long LL;
LL N;
LL A, B, K;class SegmentTree {
public:LL LChild[5000005], RChild[5000005], Max[5000005], Total, Root1;void Update(LL L, LL R, LL QueryL, LL QueryR, LL Val, LL &Root) {if (!Root) Root = ++Total;if (QueryL <= L && R <= QueryR) {Max[Root] = std::max(Max[Root], Val);return;}LL Mid = (L + R) / 2;if (QueryL <= Mid) Update(L, Mid, QueryL, QueryR, Val, LChild[Root]);if (QueryR > Mid) Update(Mid + 1, R, QueryL, QueryR, Val, RChild[Root]);}LL Query(LL L, LL R, LL Val, LL Root) {Max[Root] = std::max(Max[Root], Val);Val = std::max(Max[Root], Val);if (L == R) return Max[Root];LL M = (L + R) / 2, Ans = 0;if (LChild[Root]) Ans += Query(L, M, Val, LChild[Root]);else Ans += (M - L + 1) * Max[Root];if (RChild[Root]) Ans += Query(M + 1, R, Val, RChild[Root]);else Ans += (R - M) * Max[Root];return Ans;}
} C1894_T7;int main() {std::cin >> N;for (int i = 1; i <= N; i++) {std::cin >> A >> B >> K;C1894_T7.Update(1, 100000000, A, B - 1, K, C1894_T7.Root1);}std::cout << C1894_T7.Query(1, 100000000, 0, C1894_T7.Root1) << '\n';return 0;
}

这篇关于集训总结（年前）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---