Exercise-enhanced sequential modeling for student performance prediction

写在前面：

本篇区别于前面阅读的文献。普通的模型输入只有习题的信息，本文模型输入另外加入了习题文本描述信息。

1 摘要

在在线教育系统中，为了向学生提供主动服务（例如个性化习题推荐），一个关键的需求是预测学生在未来运动活动中的表现（例如分数）。现有的预测方法主要是利用学生的历史习题记录，其中每个习题通常表示为人工标注的知识概念，习题文本描述中包含的更丰富的信息仍有待开发。在本文中，我们提出了一种新颖的习题增强循环神经网络 (EERNN) 框架，通过充分利用学生的做题记录和每个习题的文本来预测学生的表现。具体来说，为了对学生的习题过程进行建模，我们首先设计了一个双向 LSTM，以从文本描述中学习每个习题表示，而不会丢失任何专业知识和信息。然后，我们提出了一种新的 LSTM 架构，通过结合习题表示来跟踪学生在顺序习题过程中的状态（即知识状态）。为了做出最终预测，我们在 EERNN 下设计了两种策略，即具有马尔可夫属性的 EERNNM 和具有注意力机制的EERNNA。对大规模真实世界数据的广泛实验清楚地证明了 EERNN 框架的有效性。此外，通过结合习题相关性，EERNN 可以从学生和习题的角度很好地处理冷启动问题。

2 引言

在现状的教育体系中，学生可以在做题过程中得到适当的指导，个性化获取知识。图 1 显示了一个典型学生的此类过程的示例。通常，当发布习题（例如，e1）时，学生会阅读其文本并应用知识来回答它。在此过程中，学生 s1 总共做了四次习题。为了给学生提供可以自主学习的环境，例如，学习补救建议和个性化习题建议，一个关键的需求是预测他们的表现（例如，分数），即预测学生是否能够正确回答习题（例如，e5）。

在文献中，从教育心理学和数据挖掘领域预测学生表现有很多努力，例如认知诊断、知识追踪、矩阵分解和深度学习。通常，大多数方法都致力于对学生做题记录进行建模以进行预测。但是，它们只是将每个习题表示为知识概念，例如，图 1 中的习题 e1 表示为概念“功能”。这些特定于知识的概念通常由实践中的专家（例如教师）标记。同时，这些人工表示无法区分习题的个体特征（例如难度），从而导致服务器信息丢失，例如习题 e1 和 e3 因文本而异（e3 比e1) 尽管它们都标有“Function”。为此，在本文中，我们认为将学生的习题记录和每个习题的文本结合起来是有益的，这样可以更准确地预测学生的表现。

目前方法存在的问题：首先，缺乏统一的习题表示方式。其次，追踪长期的知识状态。最后，冷启动问题

3 EERNN 框架

3.1 问题定义及方法概述

在在线教育系统中，有 S 代表学生和 E 代表做的习题。将每个学生的做题记录为 $s_i=\{(e_1^i,r_1^i),(e_2^i,e_2^i),\dots ,(e_T^i,r_T^i)\}$，其中 $e_j^i$ 表示学生 i 解决的第 j 个习题，$r_j^i$ 表示相应的分数。一般情况下，如果学生 i 对习题 j 的回答正确，$r_j^i$等于 1，否则等于 0。除了学生习题过程的日志外，我们还给出了习题的文字说明。形式上，每个习题 $e_i$与一个单词序列组合为 e i = { w 1 i , w 2 i , … , w M i } e_i=\{w_1^i,w_2^i,\dots ,w_M^i\} ei​={w1i​,w2i​,…,wMi​}。为简单起见，我们使用 $s=\{(e_1,r_1),(e_2,r_2),\dots ,(e_T,r_T)\}$ 和 e = { w 1 , w 2 , … , w M } e=\{w_1,w_2,\dots ,w_M\} e={w1​,w2​,…,wM​}分别表示每个学生进程 $s_i$ 和每个习题文本 $e_i$。

给定每个学生的做题日志和从 1 到 T 的每个习题的文本描述，目标是训练一个统一的模型 M，该模型可用于预测下一个习题 $e_{t+1}$的分数 ${\tilde{r}}_{T+1}$。

图 2 显示了我们研究的解决方案概述。在训练阶段,通过建模所有学生的做题记录和习题文本信息训练模型EERNN。之后，EERNN 可以根据每个学生的个人序列习题记录来预测每个学生在未来习题中的表现。

具体来说，EERNN 是一个通用框架，我们可以在其中根据不同的策略预测学生的表现。如图 3 所示，我们在 EERNN 下提出了两种实现，即具有马尔可夫属性的 EERNNM 和具有注意机制的 EERNNA。两种模型具有相同的模拟学生习题记录的过程，但遵循不同的预测策略

3.2 EERNN的建模过程

EERNN 框架中建模过程的目标是用输入 s 对每个学生的习题序列进行建模。从图 3 可以看出，该过程包含两个主要组件，即习题嵌入和学生嵌入。

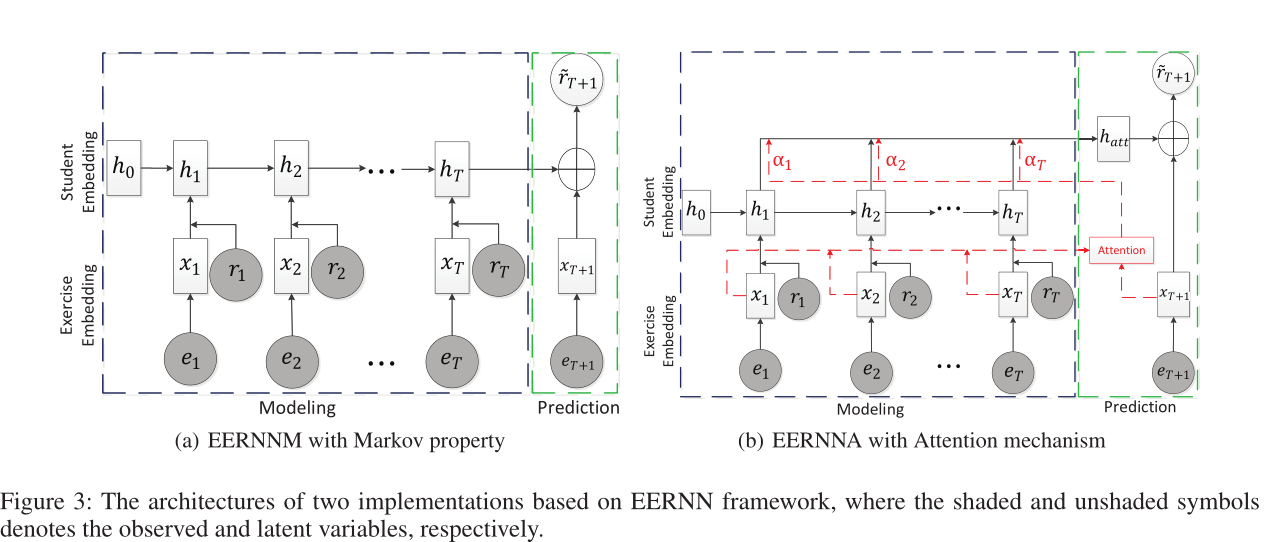
3.2.1 习题嵌入(Exercise Embedding)

如图 3 所示，给定学生习题过程 $s=\{(e_1,r_1),(e_2,r_2),\dots ,(e_T,r_T)\}$，习题嵌入 自动从其文本输入 $e_i$ 中学习每个习题 $x_i$ 的语义表示。

图 4 显示了习题嵌入的详细技术。具体来说，给定习题的文本描述，其中包含 M 个单词序列 e = { w 1 , w 2 , … , w M } e=\{w_1,w_2,\dots ,w_M\} e={w1​,w2​,…,wM​}，我们首先取 Word2vec 将习题 $e_i$中的每个单词 $w_i$ 转换为 $d_0$ 维预训练的词嵌入向量。初始化之后，习题嵌入使用先前隐藏状态 $v_{m-1}$ 更新 $w_m$在第 m 个单词步骤的隐藏状态$v_m\in {\mathbb{R}}^{d_v}$：

其中$i_m,f_m,o_m$分别代表三个门，即输入、遗忘、输出。 $c_m$是一个单元记忆向量。 σ(x) 是非线性 sigmoid 激活函数， · 表示向量之间的元素乘积。此外，输入加权矩阵 $Z_{w\ast }^E\in {\mathbb{R}}^{d_v\times d_v}$、循环加权矩阵 $Z_{v\ast }^E\in {\mathbb{R}}^{d_v\times d_o}$ 和偏置加权向量$b_{\ast }^E\in {\mathbb{R}}^{d_v}$都是习题嵌入中的网络参数。

为了充分利用习题的上下文单词信息，我们构建了一个双向 LSTM，分别取正向和反向的单词序列。如图 4 所示，在每个词步 m 处，隐藏词状态 ${\overrightarrow{v}}_m$ 是基于先前隐藏状态 ${\overrightarrow{v}}_{m-1}$ 和当前词 $w_m$ 前向传播计算的；而反向传播用未来隐藏状态 ${\overleftarrow{v}}_{m+1}$ 和当前的词 $w_m$更新隐藏词状态 ${\overleftarrow{v}}_m$。因此，每个单词隐藏表示 $v_m$ 可以通过前向状态和后向状态的连接计算$v_m=concatenate(({\overrightarrow{v}}_m,\overleftarrow{v_m})$

之后，为了获得习题 ei 的整个语义表示，我们利用 逐元素最大池化( element-wise max pooling) 操作将 M 个单词上下文表示合并到一个全局嵌入 $x_i\in {\mathbb{R}}^{2d_v}$中，即 $x_i=max(v_1,v_2,\dots ,v_M)$ .

3.2.2 学生嵌入(Student Embedding)

学生嵌入在通过习题嵌入 从其文本$e_i$中获得每个习题表示$x_i$后，旨在对整个学生习题过程进行建模，并结合学生在不同习题步骤中的表现影响学习，我们称之为学生状态。如图 3 所示，EERNN 框架依赖于两个基本假设：（1）学生状态受习题和她获得的相应分数的影响。(2) 学生在长期的连续习题过程中有可能学习也有可能遗忘。

顺着这个思路，我们利用 LSTM 网络的变体进行学生嵌入，每个特定学生习题过程的输入 $s=\{(x_1,r_1),(x_2,r_2),\dots ,(x_T,r_T)\}$。

具体来说，在每个习题步骤 t 中，网络的输入是结合了习题嵌入 $x_t$ 和相应分数 $r_t$ 的编码。由于答对得分（即 1）和错误得分（即 0）的习题在习题过程中对学生状态的影响不同，因此我们需要找到一种适当的方法来区分这些对特定学生的不同影响。

我们首先将分值 $r_t$ 扩展到具有相同 $2d_v$维度的习题嵌入 $x_t$ 的特征向量 0 = (0, 0, . . . , 0)，然后学习组合输入向量 $\widetilde{x_t}\in {\mathbb{R}}^{4d_v}$：
$$\widetilde{x_t}=\{\begin{array}{ll}[x_t⨁0]& \text{if }{r}_t=1,\\ [0⨁x_t]& \text{if }{r}_t=0,\end{array}\text{\hspace{1em}(2)}$$
其中⊕是连接两个向量的操作。

结合学生 s = { x 1 ~ , x 2 ~ , … , x T ~ } s=\{\tilde{x_1},\tilde{x_2},\dots ,\tilde{x_T}\} s={x1​~​,x2​~​,…,xT​~​}，在她的习题步骤 t 中隐藏学生状态 $h_t\in {\mathbb{R}}^{d_h}$基于当前组合输入 $\widetilde{x_t}$ 和之前的学生状态 $h_{t-1}$按照公式(1)进行更新。

其中$Z_{\tilde{X}\ast }^S\in {\mathbb{R}}^{d_h\times 4d_v}$，$Z_{h\ast }^S\in {\mathbb{R}}^{d_h\times d_h}$和$b_{\ast }^S\in {\mathbb{R}}^{d_h}$是学生嵌入的的参数。

3.3 EERNN的预测输出

心理学发现，学生的答题情况表现取决于学生的知识掌握状态和习题本身特征。据这一发现，在 EERNN 框架下提出了两种预测策略的实现，即一个简单而有效的具有马尔可夫属性的 EERNNM 和一个更复杂的具有注意力机制的 EERNNA，

3.3.1 基于马尔可夫策略的EERNNM

对于典型的顺序预测任务，马尔可夫方法是一个很好理解和广泛使用的理论，它假设下一个状态仅取决于当前状态，而不取决于它之前的序列。基于此理论，当题目在$T+1$时刻发布给学生时，EERNNM流程是：(1) 假设学生应用当前状态 $h_t$ 来解决习题； (2) 利用习题嵌入从习题文本$e_{T+1}$中提取语义表示$x_{T+1}$； (3) 预测她在运动 $e_{T+1}$上的表现 ${\tilde{r}}_{T+1}$，公式如下为：
$$\begin{gathered} y_{T+1}=ReLU(W_1\cdot [h_T\oplus x_{T+1}]+b_1) \\ {\tilde{r}}_{T+1}=\sigma (W_2\cdot y_{T+1}+b_2)\text{\hspace{1em}(4)} \end{gathered}$$
其中$y_{T+1}\in {\mathbb{R}}^{d_y}$表示在T+1时刻由习题嵌入$x_{T+1}$和学生知识状态$h_T$的进行预测的总体表示，${\tilde{r}}_{T+1}$是最后的预测输出结果。

由于当前的学生状态 $h_T$是 学生嵌入 中基于 LSTM 的架构的最后一个隐藏状态，因此当序列较长时它可能会丢弃一些重要信息，存在（梯度）消失问题。故提出了更为复杂的预测策略，即带有注意力机制的 EERNNA，以增强重要学生状态在预测的序列习题过程中的影响。

3.3.2 基于注意力机制的EERNNA

在图 1 中，学生可能在相似的习题中得到相似的分数，例如学生 s1 正确回答了习题 e1 和 e3，这可能是因为两个习题相似，因为背后的知识概念“function”相同。

根据这一观察，如图 3(b) 中的红线所示，EERNNA 假定学生的知识状态T+1时刻是基于过于学生历史状态进行聚合后的加权和，并且认为习题$e_{T+1}$和历史习题是有一定关联的。将注意力集中的学生状态向量 $h_{att}$定义为：
$$h_{att}=\sum _{j=1}^T{\alpha }_j{h}_j,{\alpha }_j=cos(x_{T+1},x_j)$$
其中 $x_j$是第 j 个习题步骤的习题嵌入，$h_j$是相应的学生状态。余弦相似度 ${\alpha }_j$ 是注意力分数，用于衡量习题 $e_j$ 对于新习题$e_{T+1}$ 在历史中重要性

在步骤 T + 1 获得带有注意力的学生状态后，EERNNA 使用公式（4）中的类似操作预测她在习题 $e_{T+1}$上的表现。 (4) 通过将 hT 替换为 $h_{att}$

特别是通过习题嵌入，我们的注意力分数 αj 不仅从句法角度衡量习题之间的相似性，而且从语义角度捕捉相关性（例如难度相关性），有利于学生状态表示用于预测和模型解释。我们将对它们进行实验分析。

4 实验

在本节中，我们进行了广泛的实验，从各个方面证明 EERNN 的有效性：（1）EERNN 在未来和冷启动场景中针对基线的预测性能； (2) EERNN 中的注意力有效性； (3) 有意义的可视化。

4.1 数据集及实验设置

数据集：

科大讯飞提供的实验数据集，采集自应用广泛的在线学习系统智学1，该系统为高中生提供了大量的做题记录。

实验设置：

详细细节看文献吧，没有实验代码，就不详细写了。

4.2 实验结果

我们对数据集进行分区以比较所有模型对学生表现预测的结果。对于每个学生的连续习题记录，我们将开始的 60%、70%、80%、90% 的习题作为训练集，其余作为测试集。我们将所有实验重复 5 次，并使用所有指标报告平均结果，如图 5 所示。

冷启动预测：

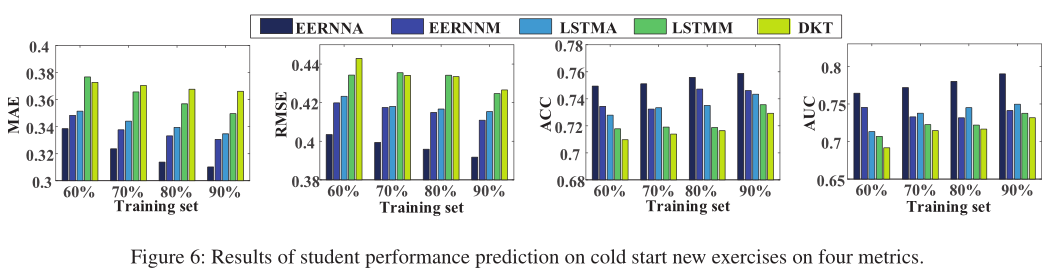
我们进行实验以从习题的角度评估 EERNN 在冷启动情况下的性能。在这里，我们只测试模型的预测结果，分别使用所有指标，在相应测试集中的新习题（从未出现在训练中）上训练 60%、70%、80%、90% 的训练集.请注意，我们不改变任何训练过程，只选择冷启动习题进行测试，因此所有测试都不需要重新训练。为了更好地说明，我们报告了所有 5 个基于深度学习的模型的结果。

如图 6 所示，也有与图 5 类似的实验观察结果，再次证明了 EERNN 框架的有效性。这些结果表明了 EERNN 框架的优越性，即在预测学生新习题的表现时，它可以很好地处理冷启动问题。

注意力机制的效果：

如第 3 节所述，我们认为具有 Attention 机制的 EERNNA 可以在学生习题过程中跟踪学生的专注状态以提高预测性能，这优于 EERNNM。为了突出注意力效应，我们使用 ACC 和 AUC 指标比较了 EERNNA 和 EERNNM（在 90% 的训练集上训练）在所有学生的不同拟合长度的相应测试集中进行预测。

从图7可以看到，当拟合长度少于40时两种策略的结果基本一样。然而，随着序列长度的增加，EERNNA 的性能逐渐提高。此外，当它超过 60 时，EERNNA 在两个指标上都显着优于 EERNNM。这一现象表明 EERNNM 对学生运动过程开始时的预测是有效的，但在序列较长时会丢弃一些重要信息。相比之下，EERNNA 通过注意力机制增强了本地学生状态，有利于预测。此外，请注意，在预测没有任何记录的学生的第一次表现的情况下（拟合长度为 0 ）。这一发现也表明，从学生的角度来看，EERNN 在解决冷启动问题时可以保证一定的效果。

可视化

特别是，EERNNA 通过注意力机制（即方程中的注意力分数 α）对每个学生的预测结果进行解释和分析的能力很大。 (5)。图 8 以实验中一名学生的注意力分数为例。在这里，EERNNA 预测学生可以正确回答习题 e20，因为她甚至在过去更难的类似习题 e4 上也得到了正确答案。从他们的课文中，我们可以得出结论，e20和e4都是“几何”习题，e4比e20更难。这种可视化暗示了 EERNNA 为结果分析和模型解释提供了一种很好的方式，这在教育应用中也很有意义。

图8：学生 EERNNA 中的注意力可视化。我们根据她过去的 19 次习题记录来预测她在 e20 上的表现（为了更好地说明，我们只展示了前 5 次习题）。右栏显示基于 e20 的所有习题的注意力得分。