三门问题（Python运算蒙提霍尔问题）

本文主要是介绍三门问题（Python运算蒙提霍尔问题），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

三门问题

1.简介

蒙提霍尔问题（英文：Monty Hall problem），亦称为蒙特霍问题、山羊问题或三门问题，是一个源自博弈论的数学游戏问题，参赛者会看见三扇门，其中一扇门的里面有一辆汽车，选中里面是汽车的那扇门，就可以赢得该辆汽车，另外两扇门里面则都是一只山羊。当参赛者选定了一扇门，主持人会开启另一扇是山羊的门；并问：“要不要换一扇门？”依照玛丽莲·沃斯·莎凡特的见解，参赛者应该换，换门的话，赢得汽车的概率是2/3。这问题亦被叫做蒙提霍尔悖论：因为该问题的答案虽在逻辑上并无矛盾，但十分违反直觉。

蒙提霍尔问题得名于主持人蒙蒂·霍尔，他主持美国的电视游戏节目《Let’s Make a Deal（英语：Let’s Make a Deal）》时，会有这样的游戏，他也确实会先开启另一扇是山羊的门，来吸引观众眼球；但他不会允许参赛者换门。蒙提霍尔问题首次出现，可能是在1889年约瑟夫·贝特朗（英语：Joseph Bertrand）所著的_Calcul des probabilités_一书中。在这本书中，这条问题被称为“贝特朗箱子悖论（英语：Bertrand’s box paradox）”（Bertrand’s Box Paradox）。另一种形式则是三囚问题（Three prisoners problem），原理是一模一样的，1959年出现在马丁·加德纳的《数学游戏》专栏中，其后被改编成各种语言的版本。

2.问题

以下是蒙提霍尔问题的一个著名的叙述，来自Craig F. Whitaker于1990年寄给《展示杂志》（Parade Magazine）玛丽莲·沃斯·莎凡特（Marilyn vos Savant）专栏的信件：

假设你正在参加一个游戏节目，你被要求在三扇门中选择一扇：其中一扇后面有一辆车；其余两扇后面则是山羊。你选择了一道门，假设是一号门，然后知道门后面有什么的主持人，开启了另一扇后面有山羊的门，假设是三号门。他然后问你：“你想选择二号门吗？”变换你的选择对你来说是一种优势吗？

Selvin在随后寄给American Statistician的信件中（1975年8月）首次使用了“蒙提霍尔问题”这个名称。

Mueser和Granberg透过在主持人的行为身上加上明确的限制条件，提出了对这个问题的一种不含糊的陈述：

1. 参赛者在三扇门中挑选一扇，他并不知道里面有什么。

2. 主持人知道每扇门后面有什么。

3. 主持人必须开启剩下的其中一扇门，并且必须提供换门的机会。

4. 主持人永远都会挑一扇有山羊的门。

   • 如果参赛者挑了一扇有山羊的门，主持人必须挑另一扇有山羊的门。

   • 如果参赛者挑了一扇有汽车的门，主持人随机（概率均匀分布）在另外两扇门中挑一扇有山羊的门。

5. 参赛者会被问是否保持他的原来选择，还是转而选择剩下的那一道门。

变换选择可以增加参赛者的机会吗？

3.解答

玛丽莲·沃斯·莎凡特在1980年代中期因跻身《基尼斯世界纪录》中的智商纪录保持人而成名（结果为185）。当时她的答复在《大观杂志》刊出之后引起举世关注。她的解答彻底违反直觉，并引起众多数学家的质疑。但随后的阐释让质疑者颜面无光。显然，莎凡特的答案是正确的，当参赛者转向另一扇门而不是继续维持原先的选择时，赢得汽车的机会将会加倍。

3.1 概率思维

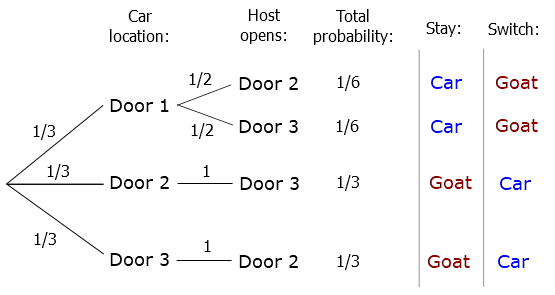
共有三种可能的情况，全部都有相等的可能性（1/3）：

1. 参赛者挑汽车，主持人挑两头羊的任何一头。变换就会失去汽车。
2. 参赛者挑A羊，主持人挑B羊。变换将赢得汽车。
3. 参赛者挑B羊，主持人挑A羊。变换将赢得汽车。

在第一个情况的表述可以分成两种情况：

• 参赛者挑汽车，主持人挑两头羊的任何一头。变换就会失去汽车。
  • 参赛者挑汽车，主持人挑A羊。变换将失败。
  • 参赛者挑汽车，主持人挑B羊。变换将失败。

在2和3两种情况，参赛者可以通过变换选择而赢得汽车。第一种情况是唯一一种参赛者保持原来选择而赢的情况。因为三种情况中有两种是通过变换选择会赢的，所以变换选择会赢的概率是2/3。

其他情况：

1. 如果主持人并不知道那扇门后面有汽车，主持人随便打开一扇门（可能主持人会直接开到汽车门，导致游戏结束）。
2. 如果主持人先从两只山羊中剔除其中一只，然后才叫参赛者作出选择的话，选中的机会将会是1/2。

3.2 逆向思维

用逆向思维的方式来理解这个选择(以主持人的角度来思考)。无论参赛者开始的选择如何，在被主持人问到是否更换时都选择更换。

1. 如果参赛者先选中山羊，换之后百分之百赢；
2. 如果参赛者先选中汽车，换之后百分之百输。

选中山羊的概率是2/3，选中汽车的概率是1/3。所以不管怎样都换，相对最初的赢得汽车仅为1/3的机率来说，转换选择可以增加赢的机会。

一些更简洁的解法：

1. 最初选羊的概率是2/3，而主持人选羊以后，你变换后选羊的概率就是你最初选车的概率，1/3。
2. 最初选车的概率是1/3，而主持人选羊以后，你变换后选车的概率就是你最初选羊的概率，2/3。
3. 最初选车的概率为1/3，车在另外两个门后的概率为2/3，主持人选羊以后，车在最后那张门后的概率还是原来两张门后有车的概率，2/3。

3.3 推理思维

三门问题是多门问题之中最难的情况。如果把三门变成一千个门，假设有车的门是987号，你选了1号门，然后主持人打开了除了你选的1号和有车的门987号之外的998扇门。改选987号门选中的概率是不改选择的999倍，即换门后选中车的概率是百分之九百九十九。

3.4 代码验证

在电脑上运行如下python代码

import randomdef monty_hall():doors = [0, 0, 1]  # 0代表山羊，1代表汽车random.shuffle(doors)  # 随机排列门的顺序choice = random.randint(0, 2)  # 参赛者随机选择一扇门# 主持人打开一扇山羊门for i in range(3):if doors[i] == 0 and i != choice:opened_door = ibreak# 参赛者选择是否换门switch = Trueif switch:for i in range(3):if i != choice and i != opened_door:choice = ibreakreturn doors[choice]  # 返回选择的门的结果（0代表山羊，1代表汽车）# 进行10000次模拟实验
num_trials = 10000
win_count_switch = 0
win_count_stay = 0for _ in range(num_trials):result = monty_hall()if result == 1:win_count_switch += 1else:win_count_stay += 1win_probability_switch = win_count_switch / num_trials
win_probability_stay = win_count_stay / num_trialsprint(f"模拟实验中换门赢得汽车的概率: {win_probability_switch}")
print(f"模拟实验中不换门赢得汽车的概率: {win_probability_stay}")

运行后可知

模拟实验中换门赢得汽车的概率: 0.6698

模拟实验中不换门赢得汽车的概率: 0.3302

这篇关于三门问题（Python运算蒙提霍尔问题）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---