【2024.1.30练习】李白打酒加强版（25分）

本文主要是介绍【2024.1.30练习】李白打酒加强版（25分），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目描述

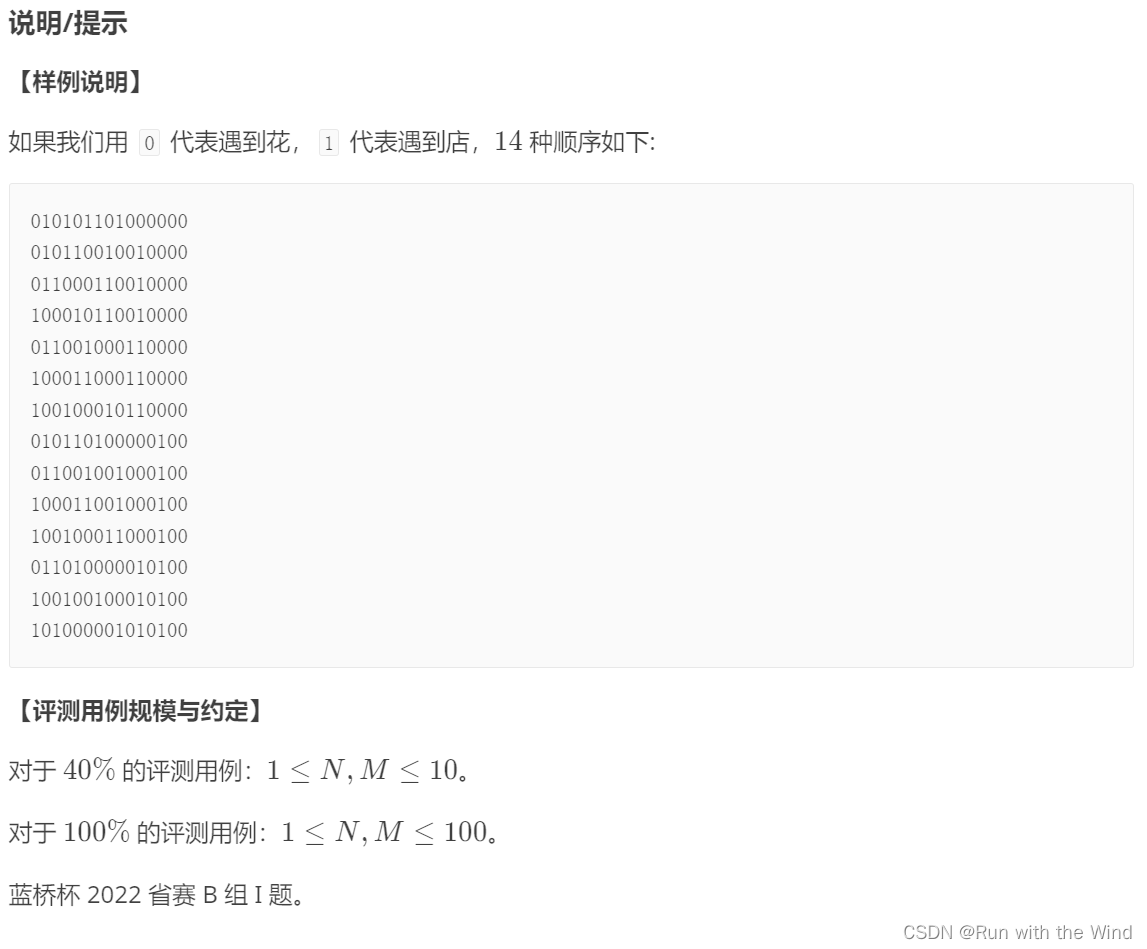
题目思路

在最多数据的情况下，有100个店100朵花，总情况为 $C_{200}^{100}$ 的天文数字，暴力枚举已经不可能实现，考虑使用动态规划解决问题。最后遇到的一定是花，所以思路更倾向于倒推。

建立二维数组 $dp[i][j]$ ，容易联想到 $i$ 为经过的花数， $j$ 为经过的店数， $dp[i][j]$ 的值代表此时酒量。但是这样 $i$ , $j$ 不能确定唯一的 $dp[i][j]$ 。且酒壶中的酒量最大可能达到 $2^{100}$ 数量级，如何储存这个大数据也是问题。

再关注数学问题本身。设第 $i$ 次遇到店添加的酒量为 $A_{i}$ ，易得：

$2+\sum_{1}^{N}A_i=M \leftrightharpoons A_1+A_2+A_3+...+A_N=M-2$

根据题意，壶中酒量最大也不会超过100斗，极大简化了数据量。

此外由数据范围可以得到M<=2或N-M>7时无解，可以拿到极端测试点的分数。

在设计状态困难的情况下先找递推关系，写几组排列组合可以得到：

设 $A(i,j)$ 为 $i$ 个店 $j$ 朵花的排列组合总数，则 $A(i,j) = A(i-1,j)+A(i,j-1)$

这样可以得到有关店数和花数的状态转移方程，然而这道题还与壶中酒量这一额外变量有关，因此考虑用三维数组存储数据。设计三维数组 $dp[i][j][k]$ ， $dp[i][j][k]$ 的值代表为经过 $i$ 个店， $j$ 朵花时壶中的酒量为 $k$ 的方案数。初始状态显然为：

$dp[0][0][k]=\begin{cases} & 1\text{ (k =2) } \\ & 0\text{ (k!=2) } \end{cases}$
$dp[1][0][k]=\begin{cases} & 1\text{ (k =4) } \\ & 0\text{ (k!=4) } \end{cases}$

$dp[0][1][k]=\begin{cases} & 1\text{ (k =1) } \\ & 0\text{ (k!=1) } \end{cases}$

实际上后两个式子都能被递推出来，是多余的。接下来建立状态转移方程：

$dp[i][j][k]=dp[i-1][j][\tfrac{k}{2}]+dp[i][j-1][k+1] \ \ \ (\tfrac{k}{2}\in \mathbb{Z})$

$dp[i][j][k]=dp[i][j-1][k+1] \ \ \ (\tfrac{k}{2}\notin \mathbb{Z})$

第二个式子省略了最后遇到的是店的情况，因为此时酒量为奇数，不可能遇到店。但是用上面的状态转移方程可能会出现 $i-1$ 或 $j-1$ 为负值的情况，因此完整的状态转移方程如下：

$dp[i][j][k]=dp[i-1][j][\tfrac{k}{2}]+dp[i][j-1][k+1] \ \ \ (\tfrac{k}{2}\in \mathbb{Z}\bigcap_{}^{}i-1,j-1\in \mathbb{N})$

$dp[i][j][k]=dp[i][j-1][k+1] \ \ \ (\tfrac{k}{2}\notin \mathbb{Z}\bigcup i-1\notin \mathbb{N})$

$dp[i][j][k]=dp[i-1][j][\tfrac{k}{2}] \ \ \ (\tfrac{k}{2}\in \mathbb{Z}\bigcap_{}^{} j-1\notin \mathbb{N})$

最终剩下的是一朵花和一斗酒。因此我们递推完成后，只需查看 $dp[N][M-1][1]$ 的值，即可获取答案。

我的代码

#include <iostream>
#include <algorithm>
using namespace std;
int dp[101][101][101];
int main() {int n;int m;cin >> n >> m;//设置初始状态int i;int j;int k;for (i = 0; i < 101; i++){if (i == 2) {dp[0][0][i] = 1;}else {dp[0][0][i] = 0;}}//动态规划for (i = 0; i <= n; i++){for (j = 0; j <= m; j++){for ( k = 0; k <= 100; k++){//分类讨论if (k % 2 == 0 && i >= 1 && j >= 1) {dp[i][j][k] = (dp[i - 1][j][k / 2] + dp[i][j - 1][k + 1])% 1000000007;}else if ((k % 2 != 0 || i <= 1) && j >= 1) {dp[i][j][k] = (dp[i][j - 1][k + 1]) % 1000000007;}else if (k % 2 == 0 && j <= 1 && i >= 1) {dp[i][j][k] = (dp[i - 1][j][k / 2]) % 1000000007;}}}}//获取答案int ans = dp[n][m - 1][1];cout << ans;return 0;
}

记得数据可能过大，每次运算都要取模。

这篇关于【2024.1.30练习】李白打酒加强版（25分）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！