摘果子【DFS】（伪AC）

本文主要是介绍摘果子【DFS】（伪AC），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目大意：

题目图片：
http://wx2.sinaimg.cn/mw690/0060lm7Tly1fwdtih8rllj30gw081q5h.jpg
http://wx1.sinaimg.cn/mw690/0060lm7Tly1fwdtih5bq8j30hb042wex.jpg
http://wx2.sinaimg.cn/mw690/0060lm7Tly1fwdtih52t0j30gu01r3yk.jpg
http://wx4.sinaimg.cn/mw690/0060lm7Tly1fwdtih5hmxj30j50gudgq.jpg

给出一棵树，选则结点$x$可以获得价值$v[x]$,但是代价是$p[x]$。可以选择这个结点仅当这个结点的父亲被选择。求代价不超过$m$时的最大价值。

---

思路：

这道题数据$n\le 1000$。但是数据太菜（不是JZOJ的），所以$O(玄学)$也是可以过的。。。
首先树形$DP$肯定是可取的。设$f[i][j]$表示以第$i$个结点为根，代价为$j$是的最大价值。方程略。
这里要讲的是$DFS$的做法。
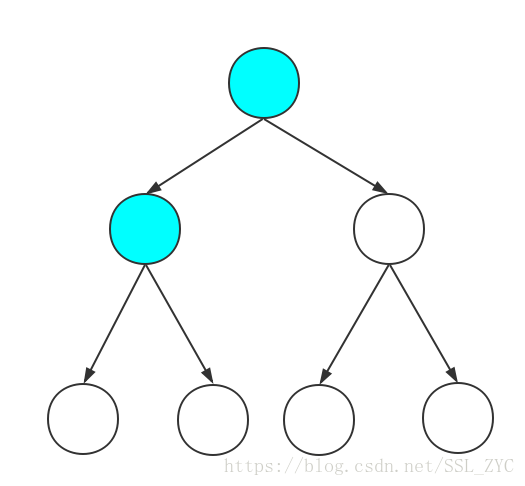
我们假设有一棵树是这样的（蓝色代表已选）：

很明显，可选的点就是父亲选了，自己没选的点。
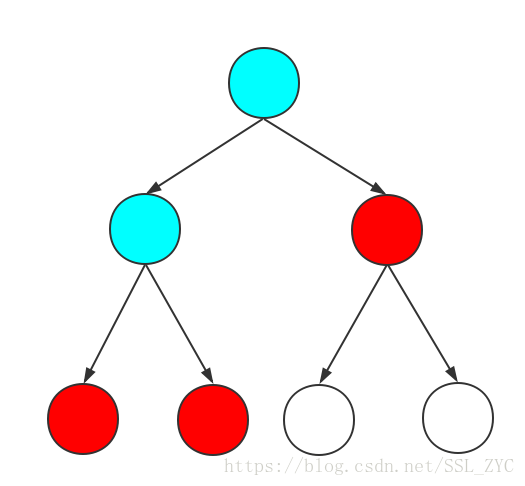
那么可选的点就有（红色）:

那么对于任意一个状态，我们先枚举每一个点，判断它是不是已经被选择，如果已经被选择，那么我们就枚举它的子节点，如果它的子节点没有被选择，就选择这个子节点，继续搜索。
时间复杂度：$O(\ge n^2)$

---

代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
#define N 2100
using namespace std;int v[N],p[N],n,m,tot,ans,head[N];
bool vis[N];struct edge
{int next,to;
}e[N*2];void add(int from,int to)
{e[++tot].to=to;e[tot].next=head[from];head[from]=tot;
}void dfs(int x,int s,int du)  //s表示价值，du表示代价
{if (du>m) return;  //代价不能超过mvis[x]=1;  //记录这个点是否走过if (s>ans) ans=s;  //记录最优答案for (int u=1;u<=n;u++)if (vis[u])  //选择过这个点for (int i=head[u];~i;i=e[i].next)if (!vis[e[i].to])  //这个选择过的点的儿子dfs(e[i].to,s+v[e[i].to],du+p[e[i].to]);vis[x]=0;
}int main()
{memset(head,-1,sizeof(head));scanf("%d%d",&n,&m);for (int i=1;i<=n;i++)scanf("%d%d",&v[i],&p[i]);int x,y;for (int i=1;i<n;i++){scanf("%d%d",&x,&y);add(x,y);add(y,x);}ans=-1e9;dfs(1,v[1],p[1]);printf("%d\n",max(ans,0));
}

这篇关于摘果子【DFS】（伪AC）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---