jzoj3034. 【NOIP2012模拟10.17】独立集

本文主要是介绍jzoj3034. 【NOIP2012模拟10.17】独立集，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目

Description

对于一棵树，独立集是指两两互不相邻的节点构成的集合。例如，图1有5个不同的独立集（1个双点集合、3个单点集合、1个空集），图2有14个不同的独立集，图3有5536个不同的独立集。

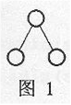
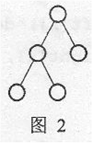
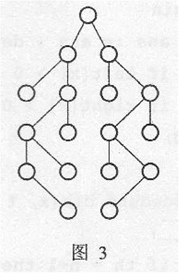
Input

第一行一个正整数n，表示点的数量。n最大为100000。
接下来n-1行，有两个整数a、b，表示编号为a、b的两个点之间有一条边，其中a、b大于等于1，小于等于n。

Output

输出一行，包含一个整数，表示独立集的数量。由于这个数很大，你只需要输出这个数除以10081的余数。

Sample Input

17
1 2
1 3
2 4
2 5
3 6
3 7
5 8
5 9
7 10
7 11
8 12
8 13
10 14
10 15
12 16
15 17

Sample Output

5536

分析

CODE

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;const int mo=10081;
int n,k,b[200010];struct llx{int x,y;
}a[200010],f[200010];void dp(int fa,int x){f[x].x=f[x].y=1;int i=b[x];while (i){if (a[i].x!=fa){dp(x,a[i].x);f[x].x=(f[a[i].x].y*f[x].x)%mo;f[x].y=((f[a[i].x].x+f[a[i].x].y)*f[x].y)%mo;}i=a[i].y;}
}int main(){scanf("%d",&n);for (int i=1;i<n;i++){int x,y;scanf("%d%d",&x,&y);k++;a[k].x=y;a[k].y=b[x];b[x]=k;k++;a[k].x=x;a[k].y=b[y];b[y]=k;}dp(-1,1);printf("%d\n",(f[1].x+f[1].y)%mo);return 0;
}

这篇关于jzoj3034. 【NOIP2012模拟10.17】独立集的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---