效率高的B树系列

本文主要是介绍效率高的B树系列，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

前面我们所学习到的数据结构，只能用来存储少量的数据，因为内存大小是非常有限的，一般情况下，也就几十个G，面对海量数据时，也就只能加载少部分数据到内存，其它的都存在磁盘，而与磁盘交换，即IO，速度是非常慢的

如下图，以二叉平衡树为例，树节点存的是磁盘中数据的地址，当数据量非常庞大时，这棵树的高度也就非常高，而内存中，为了存储更多的数据，每个节点就不存储关键字，只存储磁盘地址，所以可能每到一层，就需要进行一次磁盘IO，所以就需要进行高度次磁盘IO，效率很低

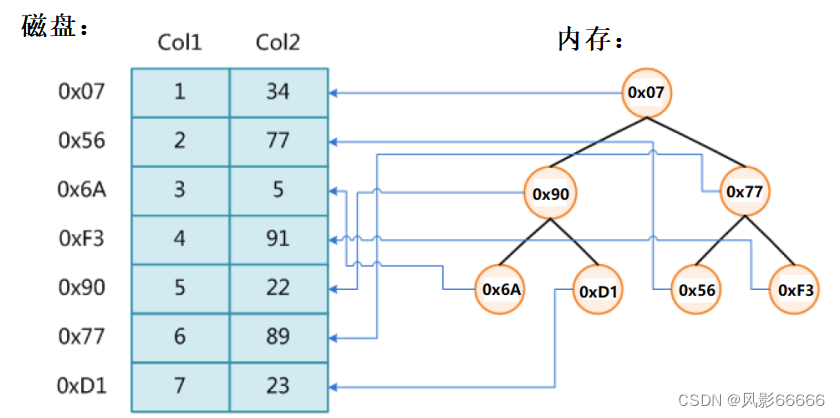
而使用哈希表，效率虽然是O(1)，但在一些极端场景下，某个位置冲突很多，导致访问次数剧增

B树

概念

为了解决前面所说的问题，R.Bayer和E.mccreight提出了B树，B树是一棵多叉平衡搜索树，如下图，B树中一个节点，存储多个关键字，这里的关键字一般也是磁盘地址，磁盘查找效率低，在于寻址慢，而B树，从两方面解决二叉平衡树的问题，第一个是从二叉变多叉，树的高度也就被降低了很多，第二个是每个节点存储多个关键字及映射的值

性质

一颗M阶(m>2)的B树，是一颗平衡的M路平衡搜索树，可以是空树，性质如下：

根节点至少有两个孩子

每个分支节点都包含k-1个关键字和k个孩子，ceil(m/2) <= k <= m，ceil是向上取整函数

每个叶子节点都包含k-1个关键字，ceil(m/2) <= k <= m

所有的叶子节点都在同一层

每个节点中的关键字从小到大排列，节点中k-1个元素正好是k个孩子包含的元素的值域划分

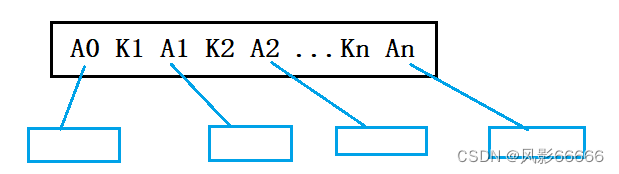
每个节点的结构为：(n，A0，K1，A1，K2，A2，… ，Kn，An)，Ki(1<=i<=n)为关键字，且Ki < Ki + 1 (1<=i<=n-1)，Ai(0<=i<=n)为指向子树根节点的指针，且Ai所指子树所有节点中的关键字均小于Ki + 1，n为节点中关键字的个数，满足ceil(m/2)-1<=n<=m-1

插入数据分析

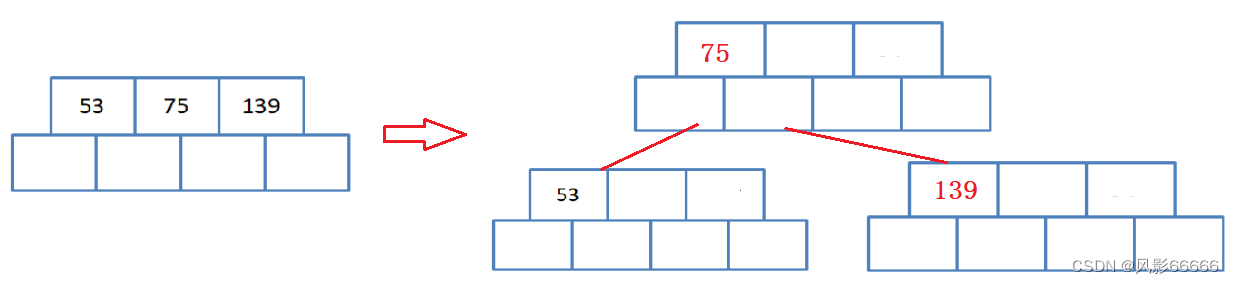
为了简单起见，这里M=3，且将节点的孩子个数和关键字个数均在原来的基础上多加1个，如下图

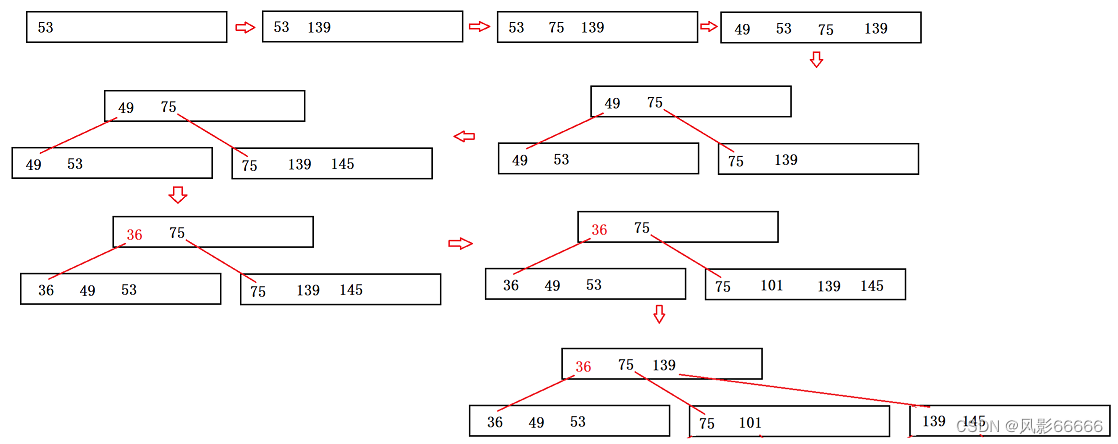
插入53、139、75，如下图，按照类似插入排序的方式，保持关键字有序

上面关键字已经满了，就需要进行分裂，将关键字中的中位数提出来插入到新建的父节点中，同时新建一个兄弟节点，将一半关键字分给兄弟节点，并将对应的一半孩子节点也分给兄弟，最后父节点指向两个孩子节点

插入49，145，从根节点开始查找，比它小，就在左边节点，比它大就往后继续走

插入36

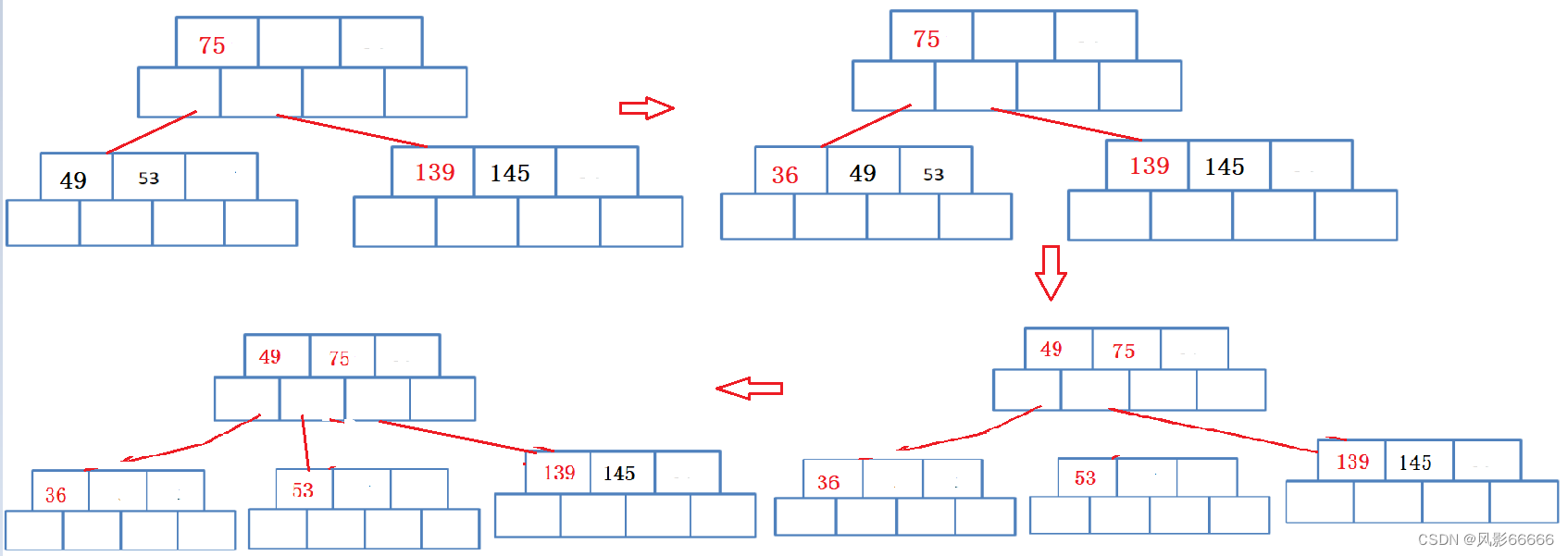
插入101

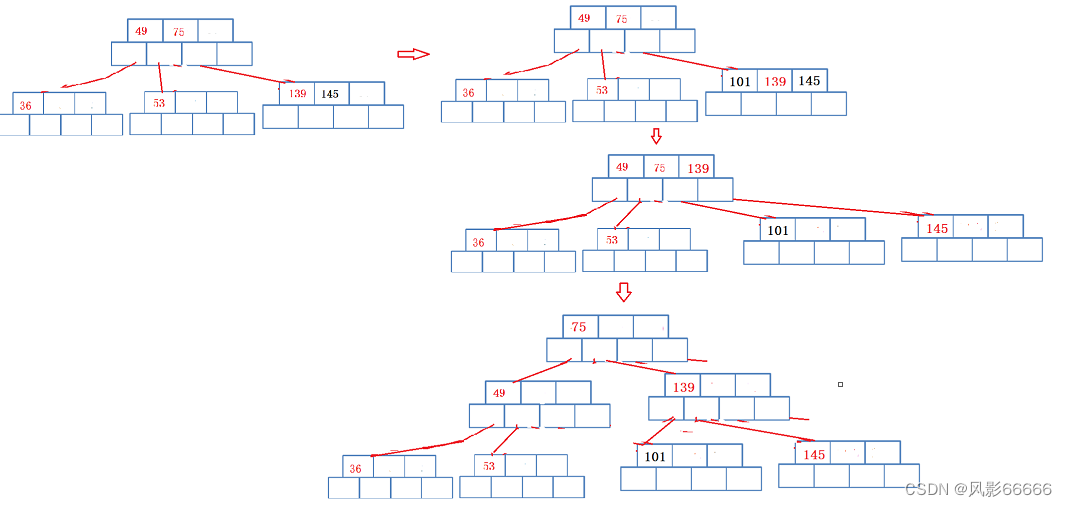
综上所述，可以看出，B树的插入过程，是一个自左向右，自底向上的过程，当节点关键字满了就分裂，然后往上插入节点，再满，就再分裂，依次类推

代码实现

为了便于分裂，多给了一个孩子和一个关键字，同时给一个父节点指针，便于后面插入节点

给定一个根节点


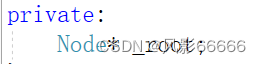
查找关键字，如果待插入的关键字小于当前节点的关键字，就直接跳到当前节点的孩子节点；如果是大于当前节点的关键字，就继续往后走；否则，要找的关键字就在当前节点，返回该节点和关键字在当前节点中的下标；找完叶子节点都没有找到，就说明不存在，返回最后找的叶子节点和-1的下标的键值对

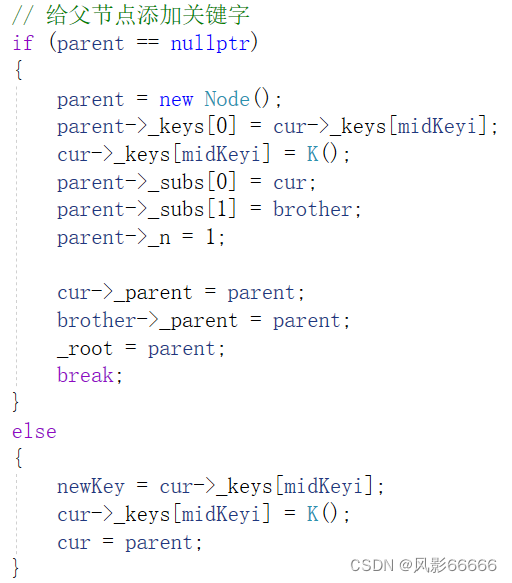
插入关键字，类似于插入排序，值得注意的是，孩子节点的位置也需要变动，同时，如果有孩子节点，还需要指向孩子节点，而孩子节点指向父亲

插入数据操作，首先，要判断是不是第一个关键字，如果是，就创建一个新节点，并将关键字插入其中即可

查找当前关键字是否存在，存在就直接返回即可

因为可能会涉及自底向上的连续分裂，所以需要多加一层死循环，如果插入关键字后的节点没有满，就直接返回即可

分裂节点，首先要找到节点的中位数的下标，然后创建兄弟节点，分一半关键字和孩子节点给兄弟，清空原节点已经不存在的关键字和孩子节点，最后更新两个节点的关键字个数

当前节点没有根节点，就创建新的根节点，然后将原节点关键字的中位数插入到根节点，同时，根节点指向这两个孩子节点，最后两个孩子节点指向父亲节点；有根节点，就将key更新为中位数，原节点更新为它的父节点，等待下次循环插入关键字

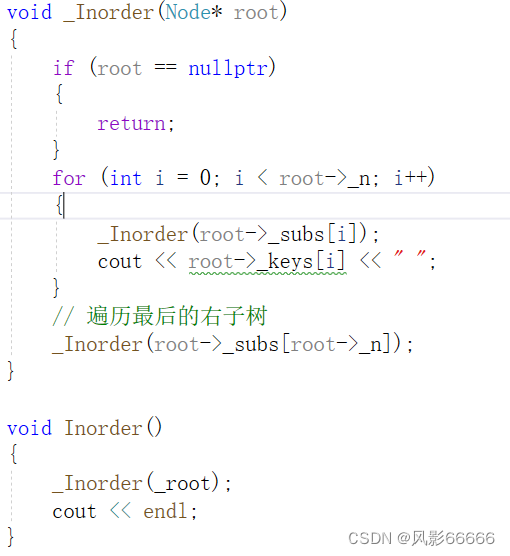
验证这棵树是否正确，可以采用中序遍历的方式，查看是否有序即可，不过，这无法判断指向父节点的指针的指向是否正确，这就需要通过监视窗口去看了

性能分析

如下图，磁盘IO的次数近似为以M为底，N为真数的对数，其中，M为树的度，N为关键字的个数

B+树

概念

B+树是B树的变形，规则和B树基本类似，但在B树的基础上进行了一些优化，如下所示：

分支节点的子树指针与关键字个数相同

分支节点的子树指针p[i]指向的关键字值大小在[k[i]，k[i+1]]之间

所有叶子节点增加一个链接指针链接在一起

所有关键字及其映射的数据都在叶子节点出现

如下图，就是一颗B+树，分支节点与叶子节点有重复的值，分支节点存的是叶子节点的索引；父节点中存的是孩子节点中的最小值做索引

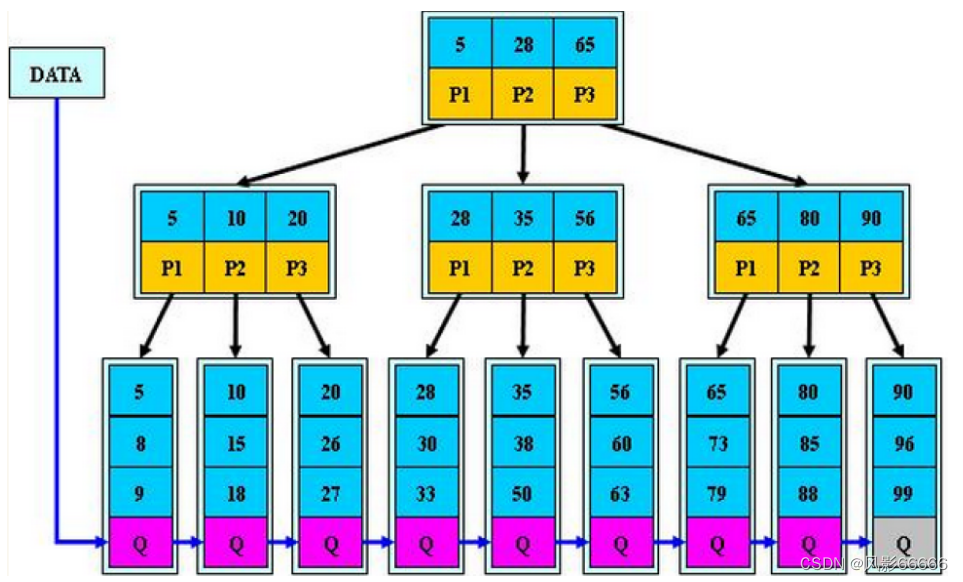
特性

所有关键字都出现在叶子节点的链表中，且链表中的节点都是有序的

不可能在分支节点中命中

分支节点相对于是叶子节点的索引，叶子节点才是存储数据的数据层

插入数据分析

插入53，139，75，49，145，36，101

应用

B+树应用于数据库索引

B*树

概念

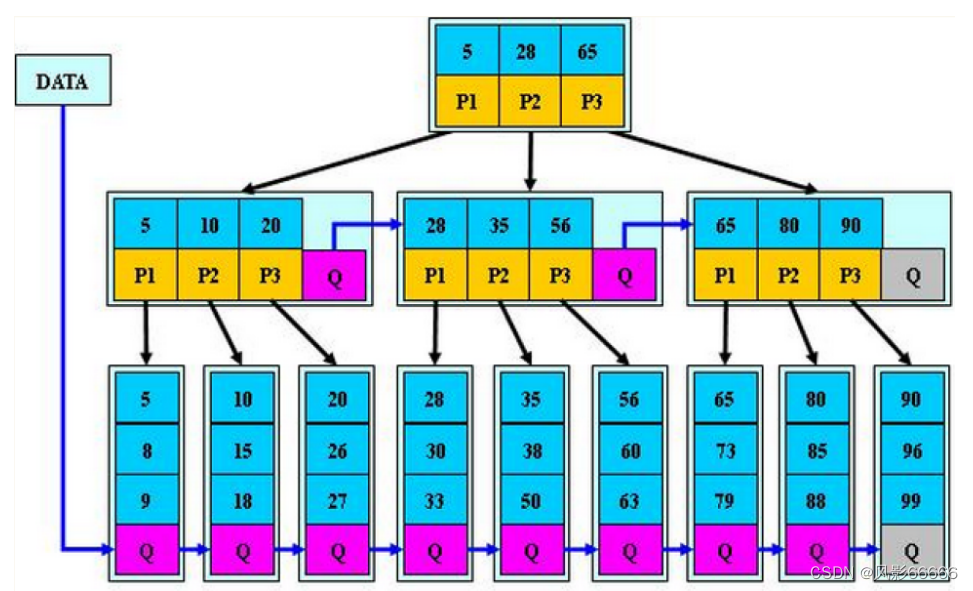
B*树是B+树的变形，在非根和非叶子节点上，再增加指向兄弟节点的指针，如下图

B*树的分裂

当一个节点满时，如果它的下一个兄弟节点未满，则将一部分数据移到兄弟节点中，再在原节点插入关键字，最后修改父节点中兄弟节点的关键字；如果兄弟也满了，则在原节点与父节点之间增加新节点，并各复制1/3的数据到新节点，最后在父节点增加新节点的指针

总结

B树系列的区别

B树：有序数组 + 平衡多叉树

B+树：有序数组链表 + 平衡多叉树

B*树：更丰满的，空间利用率更高的B+树

B树系列对比哈希和平衡搜索树

B树系列有一些隐形坏处：

空间利用率低，消耗高；

插入删除数据时，分裂和合并节点，必然要挪动数据

虽然高度更低，但在内存中而言，跟哈希和平衡搜索树是一个量级

结论：B树系列在内存中体现不出优势

这篇关于效率高的B树系列的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---