本文主要是介绍赫夫曼树(java),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、基本概念
1.1 什么是赫夫曼树
1.2 什么是权值
1.3 什么是路径
1.4 什么是带权路径长度(WPL)
1.5 举例说明
二、如何构建赫夫曼树
2.1 明确给定值
2.2 明确赫夫曼树的特点
2.3 实现赫夫曼树
2.4 关于实现赫夫曼树过程中的一点理解
三、赫夫曼树的代码实现
3.1 定义具有权值属性的结点类
3.2 构建赫夫曼树
3.3 完整代码实现
四、小结
一、基本概念
1.1 什么是赫夫曼树
- 给定N个权值作为N个叶子结点,构造一颗二叉树;
- 该树的带权路径长度(WPL)最小;
- 权值越大的结点离根节点越近;
1.2 什么是权值
- 百科:将树中结点赋给一个有着某种含义的数值。什么意思???我的理解是将数值赋给结点类中的一个变量,那么结点本身就有了权值这个属性,但是我没看懂这个定义。
1.3 什么是路径
- 从父结点到达其孩子结点或者孙子结点之间的通路;
- 若根结点的层数规定为1,那么从根结点到L层结点的路径长度为L-1;
1.4 什么是带权路径长度(WPL)
- 规定WPL为所有叶子结点的带权路径之和;
- 叶子结点的WPL = 该叶子结点的权值 * 从根结点到该叶子结点的路径长度;
1.5 举例说明

- 叶子结点上标注的值就是权值;
- 对于A,根结点为第1层,值为13的叶子结点在第3层,那么从根结点到该结点的路径长度为3 - 1 = 2;
- 对于A,值为13的叶子结点的WPL = 13 * 2 = 26;
- 那么A的WPL = WPL1 + WPL2 + WPL3 + WPL4 = 62;
- 上面三棵树中,根据赫夫曼树的定义,只有B是赫夫曼树;
二、如何构建赫夫曼树
2.1 明确给定值
- 给定的是N个带有权值的叶子结点;
2.2 明确赫夫曼树的特点
- 权值越小的结点离根结点越远,这点很关键;
2.3 实现赫夫曼树
- 定义结点类并加入权值属性,将数组中的值赋给结点;
- 将带有权值的结点加入到集合中,并从小到大排序;
- 找到权值最小的两个叶子结点,创建新的结点,其左右孩子指向这两个结点;
- 从集合中移除上述两个叶子结点,并加入新创建的结点;
- 重复上述2-4步,直到集合中只有一个元素,直接返回;
2.4 关于实现赫夫曼树过程中的一点理解
- 当叶子结点从集合中移除后,其仍在内存中,这样我们创建的这棵小树的逻辑结构还在,这就是最底下的二叉树;
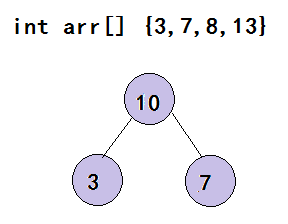
- 重新对集合中的元素排序后,按照同样的方式,能得到上一层的树结构;

- 最后得到最优二叉树,也就时赫夫曼树;

三、赫夫曼树的代码实现
3.1 定义具有权值属性的结点类
/*** 这是结点类,实现Comparable接口是为了能够排序* @author Administrator**/
class Node implements Comparable<Node> {int value;Node left;Node right;// 构造方法public Node(int value) {this.value = value;}@Overridepublic String toString() {return "" + value;}// 前序遍历public void preOrder() {System.out.print(this + " ");if (this.left != null) {this.left.preOrder();}if (this.right != null) {this.right.preOrder();}}// 这个表示从小到大@Overridepublic int compareTo(Node o) {return this.value - o.value;}
}3.2 构建赫夫曼树
// 这个方法用来构建赫夫曼树public static Node createHuffmanTree(int[] arr) {// 创建存放结点的集合List<Node> nodes = new ArrayList<Node>();// 将带有权值的结点加入集合for (int value : arr) {nodes.add(new Node(value));}// 开始构建赫夫曼树while (nodes.size() > 1) {// 对集合排序Collections.sort(nodes);// 取出权值最小的两个结点Node leftnode = nodes.get(0);Node rightnode = nodes.get(1);// 创建新的结点,构建小树Node parent = new Node(leftnode.value + rightnode.value);parent.left = leftnode;parent.right = rightnode;// 从集合中移除权值最小的两个结点,并将新结点加入nodes.remove(leftnode);nodes.remove(rightnode);nodes.add(parent);}return nodes.get(0);}3.3 完整代码实现
package practice;import java.util.ArrayList;
import java.util.Collections;
import java.util.List;/*** 这关于是赫夫曼树的练习* @author Administrator**/
public class HuffmanTree {public static void main(String[] args) {int[] arr = { 8, 3, 7, 13 };Node root = createHuffmanTree(arr);preOrder(root);}// 这个方法用于前序遍历public static void preOrder(Node root) {if (root != null) {root.preOrder();} else {System.out.println("空树,无法遍历");}}// 这个方法用来构建赫夫曼树public static Node createHuffmanTree(int[] arr) {// 创建存放结点的集合List<Node> nodes = new ArrayList<Node>();// 将带有权值的结点加入集合for (int value : arr) {nodes.add(new Node(value));}// 开始构建赫夫曼树while (nodes.size() > 1) {// 对集合排序Collections.sort(nodes);// 取出权值最小的两个结点Node leftnode = nodes.get(0);Node rightnode = nodes.get(1);// 创建新的结点,构建小树Node parent = new Node(leftnode.value + rightnode.value);parent.left = leftnode;parent.right = rightnode;// 从集合中移除权值最小的两个结点,并将新结点加入nodes.remove(leftnode);nodes.remove(rightnode);nodes.add(parent);}return nodes.get(0);}
}
/*** 这是结点类,实现Comparable接口是为了能够排序* @author Administrator**/
class Node implements Comparable<Node> {int value;Node left;Node right;// 构造方法public Node(int value) {this.value = value;}@Overridepublic String toString() {return "" + value;}// 前序遍历public void preOrder() {System.out.print(this + " ");if (this.left != null) {this.left.preOrder();}if (this.right != null) {this.right.preOrder();}}// 这个表示从小到大@Overridepublic int compareTo(Node o) {return this.value - o.value;}
}
四、小结
- 代码并不难理解,但是关于赫夫曼树的了解还太少,坚持学习,应该会有更深入的理解。
这篇关于赫夫曼树(java)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





