本文主要是介绍特征工程的千层套路?,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
数据挖掘比赛中特征工程的常见套路
前言
最近博主沉迷于天池的大数据比赛,参加了二手车交易价格预测比赛。虽然最后名次不是很高,只有266名(中间停止更新代码3到4天),但是我认为最宝贵的财富是在比赛中找到的大佬朋友,和自己获得的经验。同时,我也看到了特征工程对于比赛模型的提升空间,所以今天来给大家介绍我整理的常见特征工程对于数据的处理方式。
1.数据分箱
明确作用:将连续值转换成一个类别特征
举个栗子:这是一个小区人年龄的连续值特征:1,5,6,7,7,10·····
我们可以知道:最大值为100,最小值为1,那么我们就可以进行分组了:可以这样分1-10,11-20,····,91-100。 那么我们将这些类别分别标记为0,1,2,3,4,5,6,7,8,9,一共10个类别,作为一种类别特征出现。
那么,我们为什么要这么做呢?
优点:
1.减少噪声对数据的污染
2.防止过拟合
2.特征构造
特征构造可以使我们的模型更加复杂,推荐在模型欠拟合的时候使用。主流方法大致分为2种。
1.特征组合(提取)
特征组合,顾名思义,就是将n多个特征组合到一起去成s为一个可以协同作用的新特征。
举个栗子:有一列特征s,表示路程;特征t,表示时间。所以,根据公式:v=s/t来构造一列新的特征v,来表示速度特征。
这是按照先验知识来进行特征的组合(提取),有时候我们可能并不需要完全地按照正常的公式进行推导计算,比如说你可以组合几个特征,有可能就是一个黄金特征,对于准确率的提升很大。但是,同时模型的解释性也会变差。
特殊提醒:
遇到时间的处理方式:例如20050614,很明显这个数据的格式是YYYYMMDD,所以我们可以通过这个信息来分离出三列特征,分别是year,month,day。分别对应2005,06,14。这样我们就可以把它们当作类别特征来处理。
2.交叉特征
交叉特征会降低模型的可解释性,但是同时也可使模型变得更加复杂,使得每个特征之间的信息协同作用。
3.构建特征统计量
构建统计信息量一般先进行测试集和训练集的数据合并,然后分别构造这些统计量:计数、求和、比例、标准差。
这次比赛的前几名的大佬构造的全都是统计量。
请勿构造太多统计量,否则将会导致标签值泄漏到数据当中(leak)严重则将导致测试集和训练集差异过大
特征构造技术优劣
优势:
1.增加模型的复杂程度,防止欠拟合
2.有可能会发现一些黄金特征
劣势:
1.增加模型的复杂程度,可能导致过拟合
2.延长训练时间
3.如果构造特征不恰当,会导致模型解释性变差。
3.数据分布处理
对于标签的处理
在这次比赛中,标签值的的分布方式并没有非常完美地贴合正态分布,这对于传统线性回归模型这种有先验假设条件的模型有致命的打击,下面是对于这种情况的处理方式:
PS:我在进行搜索查询资料的时候查到了许多的方法进行处理,但是都没有提及逆变换公式,那么我也来整理一下。
1.对数变换
公式:(前提:x>0,可以自行设置偏置系数)
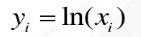
逆变换:
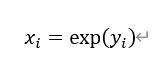
2.平方根变换
公式:(前提:x>0,可以自行设置偏置系数)
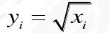
逆变换:
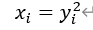
3.倒数变换
公式:(前提:x>0,可以自行设置偏置系数)
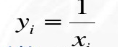
逆变换:
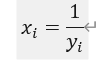
4.box-cox变换
box-cox变换和log变换很相似,但是同时效果可能会更好,下面是它的公式:
box-cox变换公式
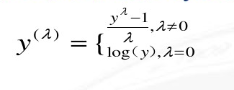
box-cox逆变换
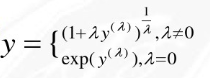
前面的公式适用于y>0的情况,下面的公式适用于y的所有取值范围:
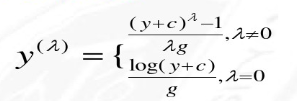
PS:以上公式来自于北京交通大学讲义ppt:Box-cox变换方法及其实现应用,还有一些不常用的方法,可以在这篇文章中找到。
未完待续,以后有时间再更新。有问题可以在评论区留言,一起讨论。
这篇关于特征工程的千层套路?的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








