本文主要是介绍POJ 1151 Atlantis,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
首先,我得吐个槽。陶叔果然是个诚实的孩子,今天的题简直坑爆了好么?
先说A题,翻了一遍题目,觉得A题(SPOJ SUB_PROB)就是个KMP的模板题,心中大喜,套模板,欲A之,怎奈何居然是WA(我还提交了三遍T_T,再不济你给个TLE我也可以接受啊)。于是重新读题,发现应该拿AC自动机来搞!!!瞄一眼Rank,分析一下局势,决定不理A题了,开了E题(Aizu 0024)。
由于E题是签到水题(按照陶叔的话来说,什么是签到题捏?签到题就是你A了以后能证明你来了的题~),果断AC。接着顺手开了F题(CodeForces 81A),发现F题也很水,是道堆栈的模拟题,以前有做过类似的题目,轻松A掉。看看表才过了不到一个小时,暗自感叹今天运气还是不错滴,喝口水,养个神,开D题(UVA 10319)。
由于英语太渣,读题貌似出现了错误,天真的以为是DFS,开心的码完代码,提交,WA。正在郁闷的时候,看到了陶叔良心发现在公告里给了Hint,尼玛,2-SAT!思路差了八十条街,而且最坑爹的是,我读错题的DFS样例居然过了!于是心情默默的不好了,关了OJ,开始各种骚扰刘文蔚学长。。。。。。
比完赛之后仔细看了看,其实C题(SPOJ RATING)挺好搞的,就是题目写得不是特别顺眼,一开始要是选这道的话,还是有可能A掉的~
好吧,吐完槽了,开始写正经东西,线段树的离散化和扫描线。
POJ上有一道题很经典,算是线段树的进阶吧,大家一起来看一下。
Description
Input
The input file is terminated by a line containing a single 0. Don't process it.
Output
Output a blank line after each test case.
Sample Input
2 10 10 20 20 15 15 25 25.5 0
Sample Output
Test case #1 Total explored area: 180.00
Source
题目意思很简单,就是让你求矩形的面积,重合的部分只算一次。解题的步骤大体来说分为三步:
1)输入数据,建树。
2)离散化:将所有的x轴坐标存在一个数组里。
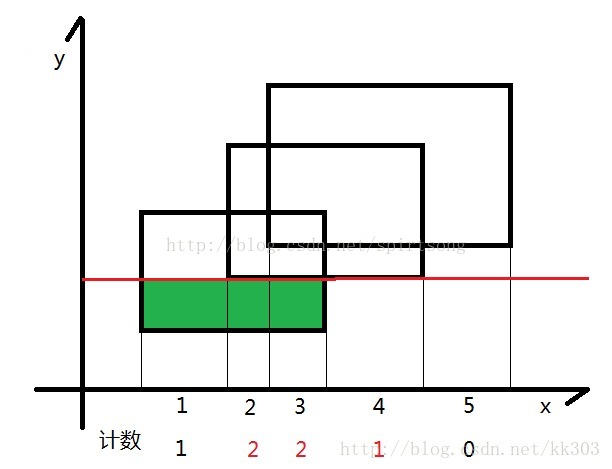
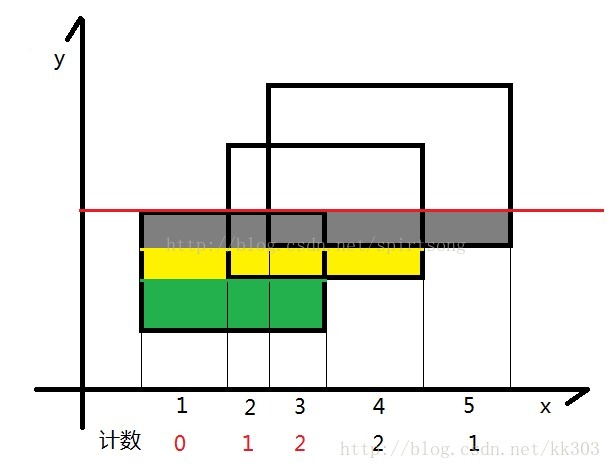
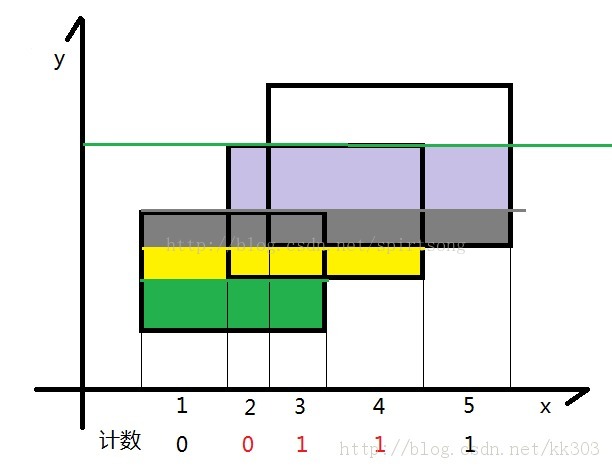
3)扫描线:从下到上扫描,更新区间计数。
图片来自:红黑联盟-kk303
下面是完整的代码:
#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
#define MAXN 405
using namespace std;struct node
{double l,r,y;//左端点,右端点,y轴高度int tp;//上下水平线标记bool operator < (node a) const// < 运算符重载,sort函数使用{return y < a.y;}
}line[MAXN << 2];int n;
double X[MAXN << 2],Times[MAXN << 2],sum[MAXN];int b_search(double x)//区间查找
{int l,r,mid;l = 0,r = n + 1;while (r - l > 1){mid=(l + r) >> 1;if (X[mid] <= x) l = mid;else r = mid;}return l;//返回离散化的区间
}void update(int x,int c,int l,int r,int now)
{if (l == r){Times[x] += c;//区间计数修改if (Times[x]) sum[now]=X[x+1]-X[x]; //若区间计数为正,得到区间长度if (!Times[x]) sum[now]=0;//若区间计数为零,不计入长度return;}int mid = (l + r )/ 2;if (x <= mid) update(x,c,l,mid,now << 1);if (mid < x) update(x,c,mid + 1,r,(now << 1) | 1);sum[now] = sum[now << 1] + sum[(now << 1) | 1];return;
}
int main()
{int i,j,T=0;double ans=0;while (~scanf("%d",&n) && n){int num=0;for (i=1;i<=n;i++){double x1,y1,x2,y2;scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);//录入矩形的对角线端点line[i*2-1].y = y1;//矩形水平线的y轴坐标line[i*2-1].l = x1;//水平线的左端点line[i*2-1].r = x2;//水平线的右端点line[i*2-1].tp = 1;//下水平线标记line[i*2].y = y2;//矩形水平线的y轴坐标line[i*2].l = x1;//水平线的左端点line[i*2].r = x2;//水平线的右端点line[i*2].tp = -1;//上水平线标记X[++num]=x1;//矩阵的左端点X[++num]=x2;//矩阵的右端点}ans = 0;n = n * 2;//每个矩阵都有上下水平线sort(X + 1,X + 1 + num);//将所有X坐标从小到大排序sort(line + 1,line + 1 + n);//将所有line按Y坐标从小到大排序memset(sum,0,sizeof(sum));//扫描线扫到的合法长度memset(Times,0,sizeof(Times));//区间的计数数组for (i = 1;i <= n;i++){ans += sum[1] * (line[i].y - line[i - 1].y);//面积 = 每一段合法长度 * 高度int l,r;l = b_search(line[i].l);//离散化,获取区间r = b_search(line[i].r) - 1;//离散化,获取区间for (j = l;j <= r;j++)update(j,line[i].tp,1,n-1,1);//扫描线更新操作}printf("Test case #%d\nTotal explored area: %.2f\n\n",++T,ans);}return 0;
}
这篇关于POJ 1151 Atlantis的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!