本文主要是介绍【嵌入式】NTC(热敏电阻)曲线拟合在嵌入式中的应用,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
NTC热敏电阻是低成本测温的有效手段,一般厂家都会提供一个阻值-温度表,通过查表获得温度值。之所以给个表,是因为阻值-温度表是非线性的。所以写程序时要把这个表写进程序,一般占用几百个字节,对于大多数MCU来说可以忽略。
今天在群里遇到一个有意思的问题,一哥们的MCU片上flash只有16K,把几百字节的NTC表加入程序后直接不够用了,咨询该怎么办。
我的办法是:通过matlab做一个阻值-温度的拟合曲线T=f( R ),让一个公式代替几百字节的表。
以我曾经用过的NTC为例,厂家给出的表如下图所示,红框框出的就是我用的NTC。

将表导入matlab,画出阻值-温度曲线如下

可以看出形状上跟指数函数比较相似,那就往指数函数上凑一下试试。用matlab的Curve Fitting工具试了几次后,发现一个函数并不能很好的拟合,于是采用分段函数。将曲线分为阻值0-22.0210K,和22.0210-195.6520K两段。
分段后,分别能拟合出拟合度99.96%和99.97%的两个函数,精度已经非常高了。拟合图如下所示
第一段:0-22.0210K
拟合公式为y = 87.07 * exp(-1.175 * x) + 82.12 * exp(-0.1201 * x)
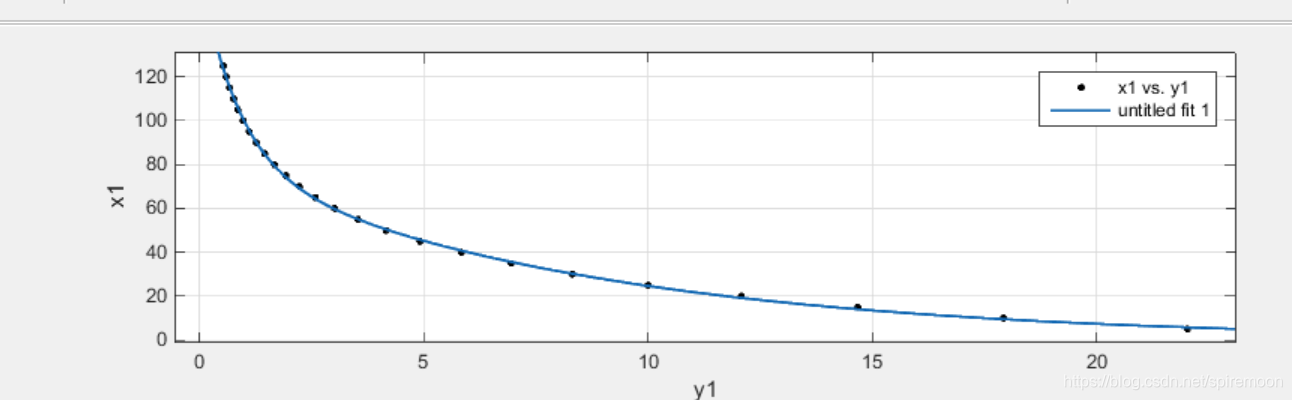
第二段:22.0210-195.6520K
拟合公式为y = -23.5 * exp( 0.002771 * x) + 54.92 * exp(-0.0281 * x)
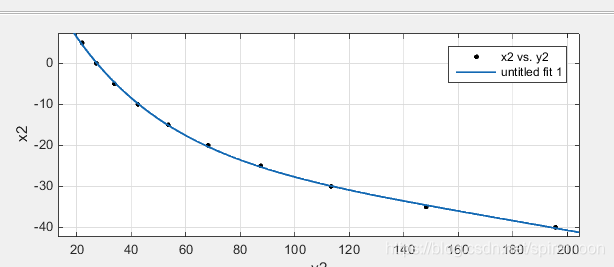
于是问题迎刃而解,通过一个分段函数,即两个公式,就能代替几百字节的表了。
误差验证
编写m脚本,输入阻值,通过上述分段函数计算温度,然后与厂家给出的表做对比。程序如下,R为厂家阻值-温度表中的阻值。
Cal = (1:34)';%计算结果
for i=1:34if(i<=10)Cal(i) = -23.5 * exp( 0.002771 * R(i)) + 54.92 * exp(-0.0281 * R(i));elseCal(i) = 87.07 * exp(-1.175 * R(i)) + 82.12 * exp(-0.1201 * R(i));end
end
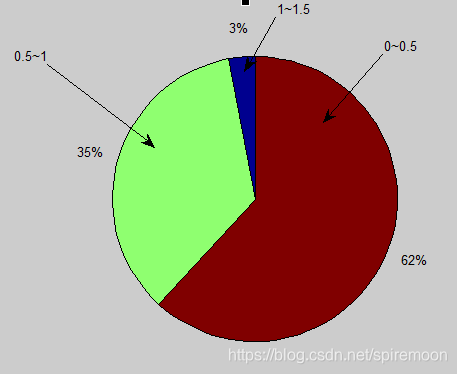
计算结束后,与厂家表中的温度做残差,然后统计误差在0-0.5,0.5-1, 1-1.5, 1.5以上的个数并作饼状图如下。可以就看出62%的误差在0.5℃以下,35%的误差在0.5~1℃之间,仅有3%的误差在1至1.5℃之间,无超过1.5摄氏度的误差。可以看出,用公式代替表,虽然起到了减小flash占用的作用,但也会引起一定的误差。但误差范围基本都在1℃以内,还是完全可以满足一些对温度精度要求不高的场合。
这篇关于【嵌入式】NTC(热敏电阻)曲线拟合在嵌入式中的应用的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






