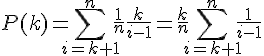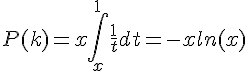第四周总结——对思维题目的理解与秘书问题

本文主要是介绍第四周总结——对思维题目的理解与秘书问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

通过这一周对思维题目以及思维资料的阅读，在遇到一个思维题时，基于目前所学，我总结了三个步骤：建模、解模、解释。首先理解题意，对所研究的问题进行整理归纳，建立模型；然后运用数学思维进行推理，解出模型；最后用语言解释所建立的模型。以下，我便由一个例子，来对思维进行我自己的解释：

Just Eat It

原题连接：Problem - 1285B - Codeforces (Unofficial mirror site, accelerated for Chinese users)

（一）对问题建立模型：有一组数列，设其和为sum，在此数列中取任意子数列段，并求其子数列段的和ans，若存在ans>=sum，则输出“no”；否则输出“yes”。

（二）解模：首先输入一组数列，并求出其和，然后求其余子数列段的和进行比较，便可得出结果。

我想可以把这个问题分成三种情况：数列中存在小于等于0的数；数列中不存在小于等于0的数；整体。

①数列中存在小于等于0的数：

因为我们选取的[l, r]区间，相当于是整个数列前面砍去一部分，后面再砍去一部分，如果我们能砍掉一段总和小于等于0或的区间或小于等于0的数，则我们的总和一定比整个数列和要大或相等。

这时需要先从数列前端与后端开始判断数列是否存在小于等于0的数，并砍去总和小于等于0的部分，即可判断。

②数列中不存在小于等于0的数：

无论如何，整体数列的和必定大于子数列的和，直接输出“yes”。

③若整体来做：

找最大子数列，直接判断最大子数列的值是否大于整体数列的总和。

我们可以锁定数列的右端点r，然后找到[1, r - 1]中的最小和位置l，则[l, r]是以r为右端点的最大连续子数列区间。我们把所有区间的和取max就可以得到整个数列的最大连续子数列和。

（三）解释：
整体来做：

#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const ll inf=999999999;
ll a[100005];
int main(){int t,n;cin>>t;while(t--){cin>>n;ll sum=0;for(int i=0;i<n;i++){cin>>a[i];sum+=a[i];}ll ans=-inf,now=0;for(int i=0;i<n-1;i++){now+=a[i];ans=max(ans,now);if(now<0) now=0;}now=0;for(int i=1;i<n;i++){now+=a[i];ans=max(ans,now);if(now<0) now=0;}if(sum>ans) cout<<"YES"<<endl;else cout<<"NO"<<endl;}return 0;
}

数列中存在小于等于0的数：

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 1; i <= (n); ++i)
using namespace std;
typedef long long m;
const int N = 1E5 + 10;
int a[N];
int main()
{int t; cin >> t;while (t--){int n;cin>>n;bool flag=0;m sum = 0;rep(i, n) {cin>>a[i];sum += a[i];if(sum<=0 and i!=n)flag=1;}sum=0;for(int i=n;i>=2;--i) {sum+=a[i];if (sum<=0) flag=1;}if (!flag) cout<<"YES"<<endl;else  cout<<"NO"<<endl;}return 0;
}

对于这个题，我考虑用排序的方法能否解出。思路：首先对数列从小到大进行排序，若数列中存在小于等于0的数，便锁定这些数的位置，判断其位置是否连续，并对其两边的数进行求和，若和达到临界（和<=0）时，便砍去这一段子数列，所得其余子数列求和与整体数列和进行比较，即可得出答案。

秘书问题

最近看了一个很有趣的问题——秘书问题，又名最优停止理论或37%

如何停止观望时间？这个理论给了一个科学的数据：当你选择到全部的37%时，你就可以停止观望，进行选择了，而在这37%之前，千万不要做选择哦，在观望到37%时，你便可以做出选择了，不然担心自己所做选择太仓促或丢掉最优选择的概率会更大。

同时也有个经典问题与之相似：麦穗理论

如果你想摘取最大的麦穗，假设有n个麦穗，你应该先将前n/e个麦穗作为参考，然后再k+1个麦穗开始选择比前面k个最大的麦穗即可。

e = 2.718281828459，1/e = 0.36787944117144。

这是有理论依据的：

假设我们碰到的麦穗有n个，我们用这样的策略来选麦穗，前k个，记住一个最大的麦穗记为d（可能是重量，也可能是体积），然后k+1个开始，只要大于d的，就选择，否则就不选择。
　　对于某个固定的k，如果最大的麦穗出现在了第i个位置（k<i≤n），要想让他有幸正好被选中，就必须得满足前i-1个麦穗中的最好的麦穗在前k个麦穗里，这有k/(i-1)的可能。考虑所有可能的i，我们便得到了前k个麦穗作为参考，能选中最大麦穗的总概率P(k)：

　　

　　设k/n=x，并且假设n充分大，则上述公式可以改为：
　　

　　对-x·lnx求导，并令这个导数为0，可以解出x的最优值，它就是欧拉研究的神秘常数的倒数——1/e。
　　所以k=n/e.