[蓝桥杯]等腰三角形

本文主要是介绍[蓝桥杯]等腰三角形，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本题目要求你在控制台输出一个由数字组成的等腰三角形。
具体的步骤是：

1. 先用1,2,3，…的自然数拼一个足够长的串
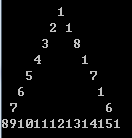
2. 用这个串填充三角形的三条边。从上方顶点开始，逆时针填充。 比如，当三角形高度是8时：
   

输入
输入存在多组数据，对于每组数据：
输入一行包含一个正整数n(3<n<300),表示三角形的高度

输出
对于每组测试数据输出用数字填充的等腰三角形。
为了便于测评，我们要求空格一律用"."代替。

样例输入
5
10

样例输出

这题比较容易想到是一道通过求解一些数学规律来完成题目的要求。但其实当我看到这道题第一个困惑的 点在于这些数字的存储。
首先这个等腰三角形肯定是逐行打印出来的，每一行的一个数字不难解决，但最后一个数字呢？由于当出现多位数时，每一位是分开的，那么也就是每行的最后一个数字是很难找到规律的（反正我找不到 ）。那么该如何解决每一行最后一个数字的存储呢？
一个可行的办法是，由于每一个等腰三角形中的数字的数量是很容易统计出来，因此我们可以先用一个数组或是字符串将所有的数字储存起来，然后从第二行开始分别从头与尾遍历，直到最后一行将剩余字符全部输出。
由于c++11中to_string的存在，因此我选择字符串存储。
接下来就是求解等腰三角形的数学规律（ i 表示行数，$1\le i\le n$）

1. 每一行一开始的点的数量：$n-i$\
2. 每一行（第一行不存在，最后一行为数字）两个数字中间的点的数量：
   $2\ast (n-1)-1=2\ast n-3$

代码如下：

#include <bits/stdc++.h>
using namespace std;
int main() {int n;cin >> n;int num = 4 * n - 4, k = 1;string str = "";while (str.length() <= num) {str += to_string(k);k++;}//l、r分别表示遍历str的头、尾int l = 0, r = num - 1;for (int i = 1;i <= n;i++) {for (int j = 0;j < n - i;j++) cout << '.';if (i == 1) cout << str[l++] << endl;else if (i != n) {cout << str[l++];for (int j = 0;j < 2 * i - 3;j++) cout << '.';cout << str[r--] << endl;}else {//最后一行连带首位两个数字一起输出for (int j = 0;j < 2 * i - 1;j++) cout << str[l++];cout << endl;}}}

这篇关于[蓝桥杯]等腰三角形的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---