【EOJ Monthly】2021.3

A：读不懂古神语的程序员不是一个合格的探险家

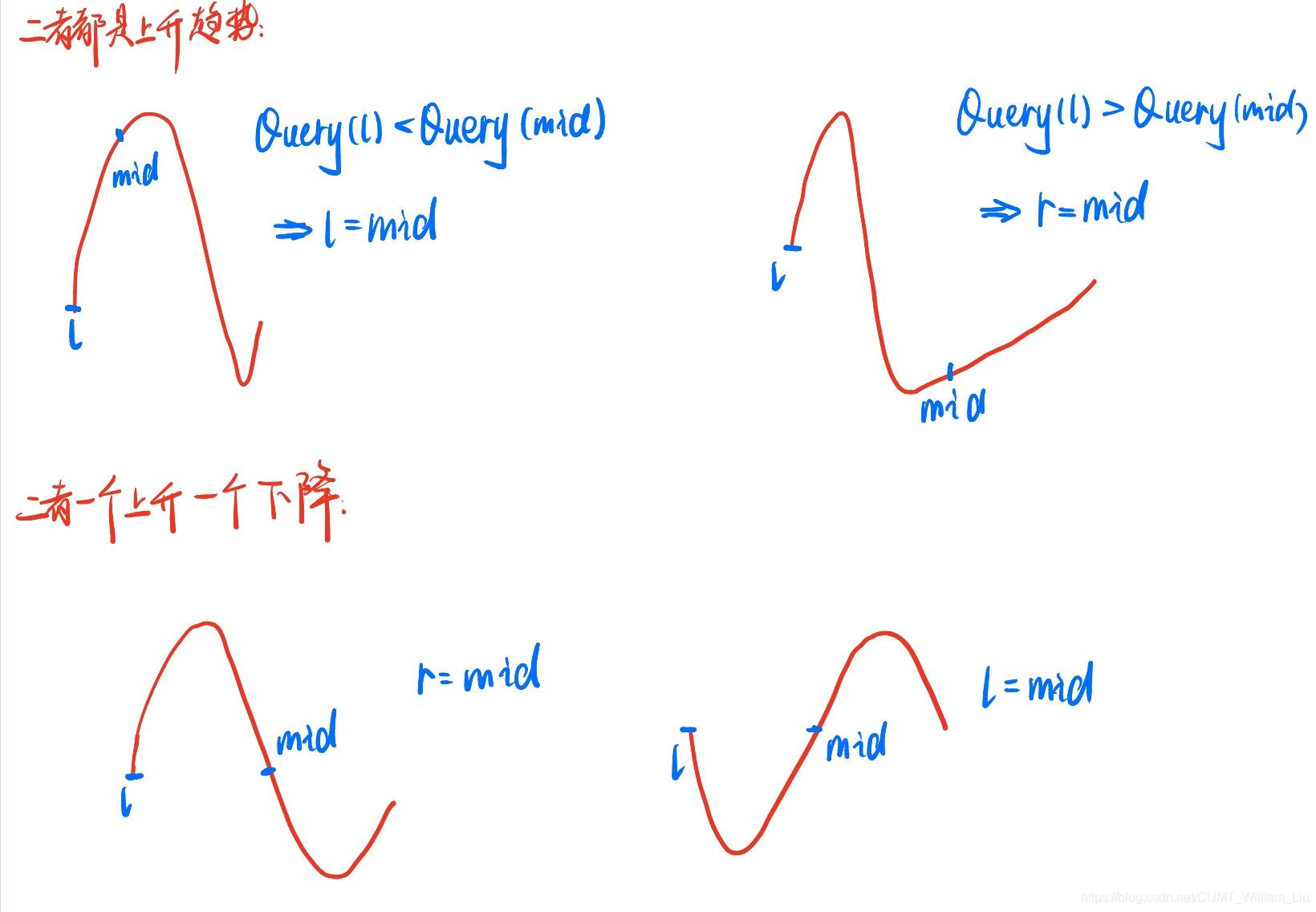
  挺好玩的一个题1。其实按照题意来说就是一个环，从最小值到最大值都是递增的，从一号结点拆开也就是一个二次函数或者三次函数，让你找最值。一开始写了一个普普通通的三分代码，其实会有一个很致命的问题就是越界的问题（针对于三次函数并不是单峰的情况）。后来发现了一种很妙的代码：就是在左端点和中点的下一个点去判断这个上升/下降趋势，然后分类讨论：

#include<bits/stdc++.h>
using namespace std;
const int maxn=(1<<20)+100;
int vis[maxn],n;
int Query(int x)
{if(vis[x]!=-1) return vis[x];printf("? %d\n",x);fflush(stdout);int num;scanf("%d",&num);if(num==(1<<n)) {printf("! %d\n",x);fflush(stdout);exit(0);}vis[x]=num;return vis[x];
}
int main()
{scanf("%d",&n);int l=1,r=1<<n;memset(vis,-1,sizeof(vis));while(l<r){int mid=(l+r)>>1;bool jud1=Query(l)<Query(l+1),jud2=Query(mid)<Query(mid+1);if(jud1 && jud2){if(Query(l)<Query(mid)) l=mid;else r=mid;}else if(!jud1 && !jud2){if(Query(l)<Query(mid)) r=mid;else l=mid;}else if(jud1 && !jud2)  r=mid;else l=mid;}
}

B：我想把我的心意叠成小小的一块塞进你的心里

  挺好玩的一个题2。其实我们很容易发现这是一个贪心题，从叶子结点开始，一层层往上折，折到不能继续折下去了就结束。但其实我们发现，对于一个结点$u$来说，如果他有$k$个子结点，那么处理一次就会到达$O(k^2)$（可以假想前面有一个空子树，然后检查一个合并一个，直到所有的子结点都被检查），然后还得递归地去检查合并后子树的子树中有没有还需要再次合并的，时间复杂度太高，而且对于链式前向星的这种存图方式来说，删边还需要很多操作（类似链表）。
  题解给出了一种很神奇的做法，就是新建一棵虚拟的树$T^{\prime }$，合并子树的操作变成了指针的来回移动，递归的同时就完成了合并的操作，步骤其实可以画图理解一下。

#include<bits/stdc++.h>
#define close ios::sync_with_stdio(false)
using namespace std;
const int maxn=1e5+100;
struct Edge{int to,w;Edge(int a,int b):to(a),w(b){}
};vector<Edge> e1[maxn],e2[maxn];
int val[maxn],p;
void DFS1(int root,int fa)
{for(Edge u:e1[root]){if(u.to==fa) continue;int rec=p;bool change=false;for(Edge v:e2[p])if(u.w==v.w && val[u.to]==val[v.to]) {change=true;p=v.to;break;}if(!change){e2[p].push_back(Edge(u.to,u.w));e2[u.to].push_back(Edge(p,u.w));p=u.to;}DFS1(u.to,root);p=rec;}
}
int DFS2(int root,int fa)
{int ans=1;for(Edge u:e2[root]){if(u.to==fa) continue;ans+=DFS2(u.to,root);}return ans;
}
int main()
{close;int n;cin>>n;for(int i=1;i<=n;++i) cin>>val[i];for(int i=1;i<n;++i){int x,y,w;cin>>x>>y>>w;e1[x].push_back(Edge(y,w));e1[y].push_back(Edge(x,w));}p=1;DFS1(1,-1);cout<<DFS2(1,-1)<<endl;
}

C：不会吧不会吧不会这道题还有同学答案错误吧

  挺好玩的一个题3。没啥能说的，直接生成一个树的数据，然后写一个bat脚本，用题目给的测试文件测试答案即可（这里我把题目给的测试文件输出结果用,隔开）。
  生成树的数据，我是先在数组中存放1~n，然后使用random_shuffle打乱，然后从第二个结点开始随机为其分配父结点的id。然后写一个bat脚本将题目给的std文件输出的结果自动进行比较（大约跑了2k次？反正我生成的树就是随机的，没啥特殊的 ）放上bat脚本。

@echo off
:looprand.exe %random% >input.txtstd.exe < input.txt > stdout.txtfor /f "tokens=1,2 delims=," %%i in (stdout.txt) do (echo %%i %%jif %%i lss %%j pause)
goto loop

D：关于小方的爆款桌游还没面世就要夭折这回事

  这个题挺一般的，一个常见的对称放置的套路。如果列数，行数的一半都是奇数的话，就放正中心，后面跟着别人对称摆放一定赢；如果不是中心的话，别人跟着你对称摆放就一定输。

E：蟹老板的梦幻传送门真的能让宅男走出家门吗

  挺好玩的一个题4。题解给的是先排个序，然后我们可以假设存在某个分界线$a_i\in [1,n]$，左区间都走左边的传送门，右区间都走的右边的传送门，那么自然我们就得把传送门设在区间的中间：$X=\frac{a_1+a_i}{2},Y=\frac{a_{i+1}+a_n}{2}$，然后我们就可以得到$d(i,j)=max(X-a1+a_n-Y,a_i-a1,a_n-a_{i+1})=max(\frac{a_i-a_1+a_n-a_{i+1}}{2},a_i-a_1,a_n-a_{i+1})=max(a_i-a_1,a_n-a_{i+1})$，这样问题就可以在$O(n)$的时间内解决了。