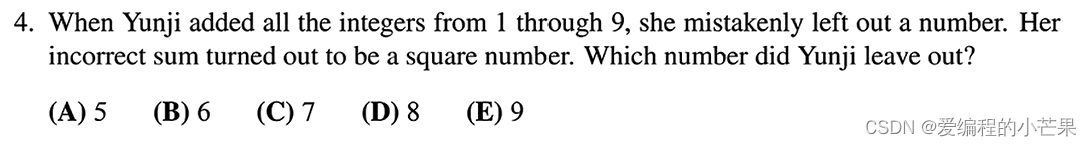全网最详细丨2024年AMC8真题及答案来了

本文主要是介绍全网最详细丨2024年AMC8真题及答案来了，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

真题回忆

真题解析

结尾

前言

相信大家都已经知道今年AMC8出事情了吧，但最重要的还是要从中学到新知识。

听说今年考生被提前12分钟强制交卷了，肯定因为试题泄露了。

最新回复：我们这边已经退费了

真题回忆

需要word文档的请私信

真题解析

1. 这一道题非常简单，只需观察个位即可，个位变化如下：
2→0→8→6→4→2 故选B

2.没有什么特别好的方法，硬算即可，记得先约分再算。

4+2.5+0.04=6.54 故选C

3.这一题问的是灰色面积，利用大减小，分别求出两个灰色L形再相加。

7×7-4×4=(7+4)(7-4)=33

10×10-9×9=(10+9)(10-9)=19

33+19=52

故选E

4.这是一道思维题。题目说Yunji把1-9加起来，但漏了一个，结果是平方数，问漏的数。

我们可以先把1加到9的和给算出来：1+2+3+……+9=(1+9)*9÷2=45

而题目漏了一个数，我们把这个漏完后的序列范围给找出来：

漏9(最小)：45-9=36 漏1(最大)：45-1=44

也就是说漏完后的序列范围在36~44之间。

而36~44之间有且仅有一个平方数——36=6×6。

所以漏的数是9，故选E。

5.暴力枚举，注意题目中的cannot。
先看第一个答案5，5=1+4=2+3，而2×3=6，答案A正确。

再看第二个答案6，6=1+5=2+4=3+3，并没有乘积为6的，答案B错误。

接着看第三个答案7，7=1+6=2+5=3+4，而1×6=6，答案C正确。

然后看第四个答案8，8=1+7=2+6=3+5=4+4，而2×6=12，答案D正确。

最后看第五个答案9，9=1+8=2+7=3+6=4+5，而3×6=18，答案E正确。

故选B

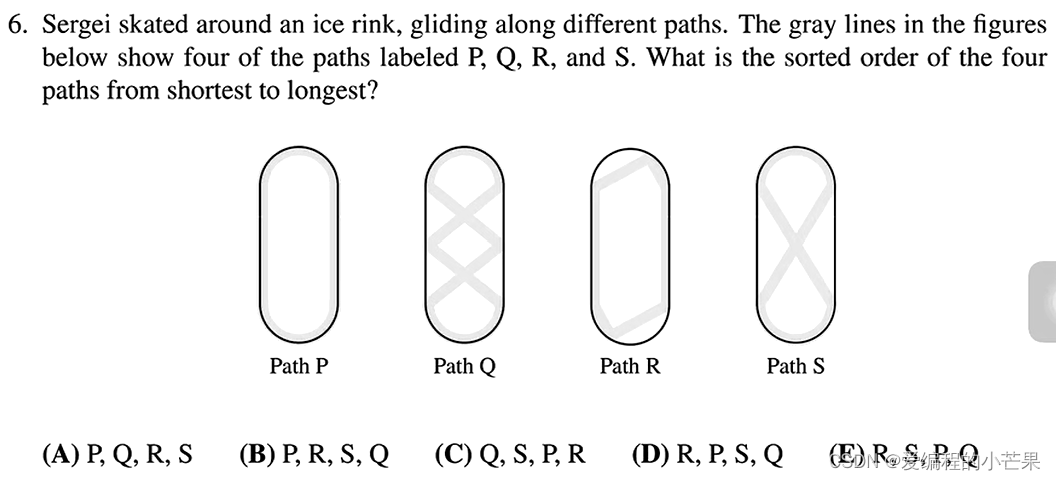
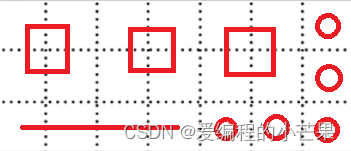
6.这是一道观察题目，通过观察很容易发现Q最长，S第二长，剩下的P和R需要仔细研究。

因为圆的半周长是肯定大于自身的直径的，所以R最短，P第二短。

注意：这道题问的是从短到长，千万不要选成C了！！！

故选D

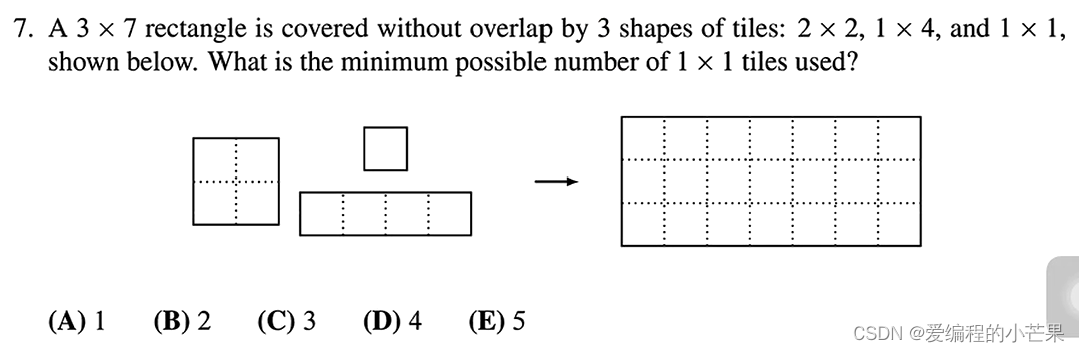
7.动手画一画就能得出答案：

故选E

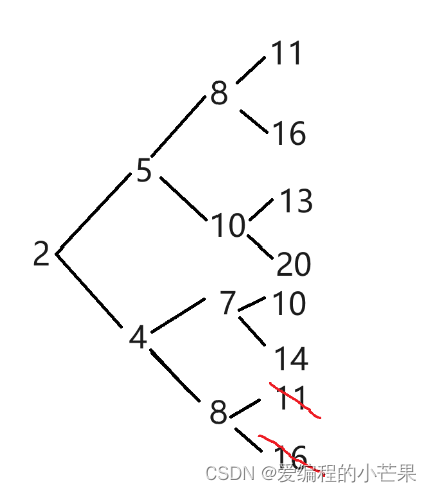
8.可以画一个二叉树，再去掉相同的。每个树枝往上代表+3，往下代表×2.

数一数，共6种，故选D。

9.简单通比。

红 : 绿 : 蓝=1 : 2 : 4
总弹珠数应该是(1+2+4)的倍数，排除ABCD。

故选E

10.基础计算题，1980是338，每年增长1.5，问2030年。

(2030-1980)*1.5+338≈414

故选B

11.先求出三角形的底边长为(11-5)=6。

根据三角形面积公式，可得出6(y-7)=24，解得y=11。

故选D

12.解：设第一个鱼缸有x条孔雀鱼。

x+(x+1)+(x+1+2)+(x+1+2+3)=90

4x+10=90

4x=80

x=20

x+6=26

故选E

13.因为兔子跳来跳去最终要回到原地，也就是说要有三个up和三个down。

很容易想到标数法（最高三层）：

故选B

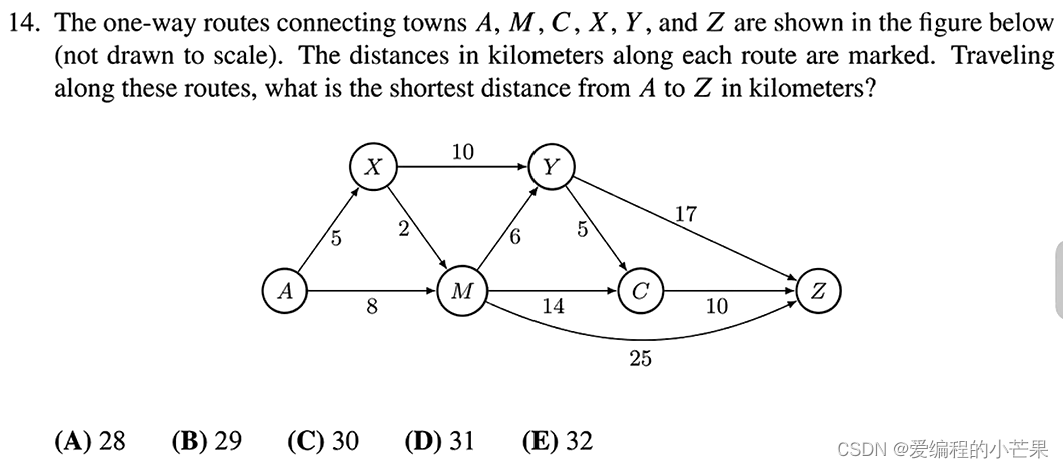
14.最优问题。

最优路线为：

5+2+6+5+10=28，故选A

15.思维题，先化简算式。

8 × FLYFLY = BUGBUG

8 × FLY × 1001 = BUG × 1001

8 × FLY = BUG

要想FLY最大，且FLY和BUG个个数位不同，F最大也只能是1，L=2，Y=3。

BUG = 123 × 8 = 984

123 + 984 = 1107

故选C

16.思维题，最优问题。

首先要知道1-81中有多少个3的倍数，每三个数中会有一个，所以共有27个。

现在题目要求我们让尽可能少的行和列是3的倍数，那么这些数该放在哪里呢？

情况1：

共“祸害”了9个行和3个列，3+9=12。

情况2：

共“祸害”了5个行和6个列，5+6=11。

11<12 故选D

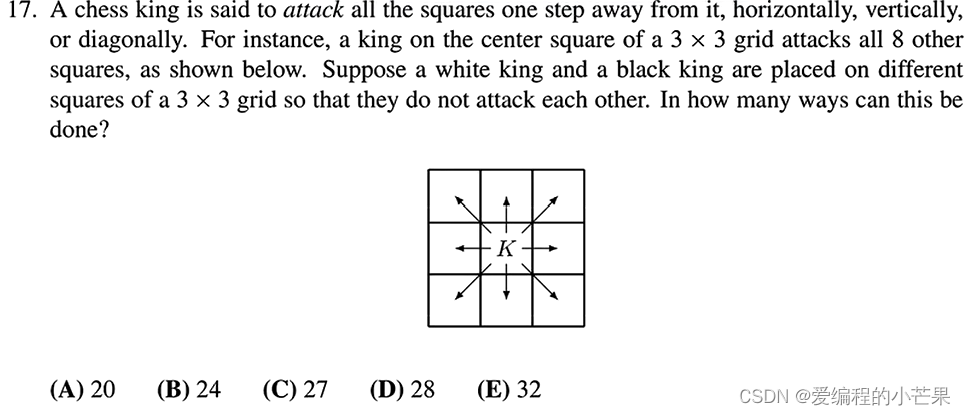
17.分类讨论。

题目说在3×3的格子中放一个黑一个白，每个子的攻击方式是周围一圈（类似于扫雷）。

问有多少种摆放方法才能让两个子互不攻击。

我们先不考虑棋子的颜色。

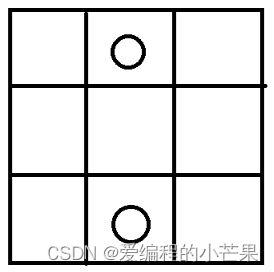
情况一（两子在边上）：



共有四条边，所以有四种。

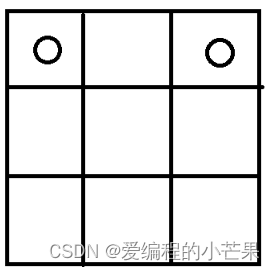
情况二（两子成“日”字）：



一条边有两组，有四条边，2×4=8(种)

情况三（两子对角）



两条对角线，共两种。

情况四（两子对边）



两条对边，共两种。

(4+8+2+2)×2=32(种)

故选E

20.观察能力。

通过观察我们可以发现以任意一个定点延出去的三个边上的三个定点都可以组成一个等边三角形。

而链接P点的有三条边，所以会有三个等边三角形包含P点，故选D

21.差的只数必定是(3-1)和(4-1)的公倍数，排除ACD。

剩下两个选项，试一试即可。

12÷(3+1)×3=9 12-9=3

9-3+5=11 3+3-5=1

很显然B不对，故选E

22.老题目了，圆面积计算。

(2×2-1×1)π÷0.015≈3×3÷0.015≈600

故选B

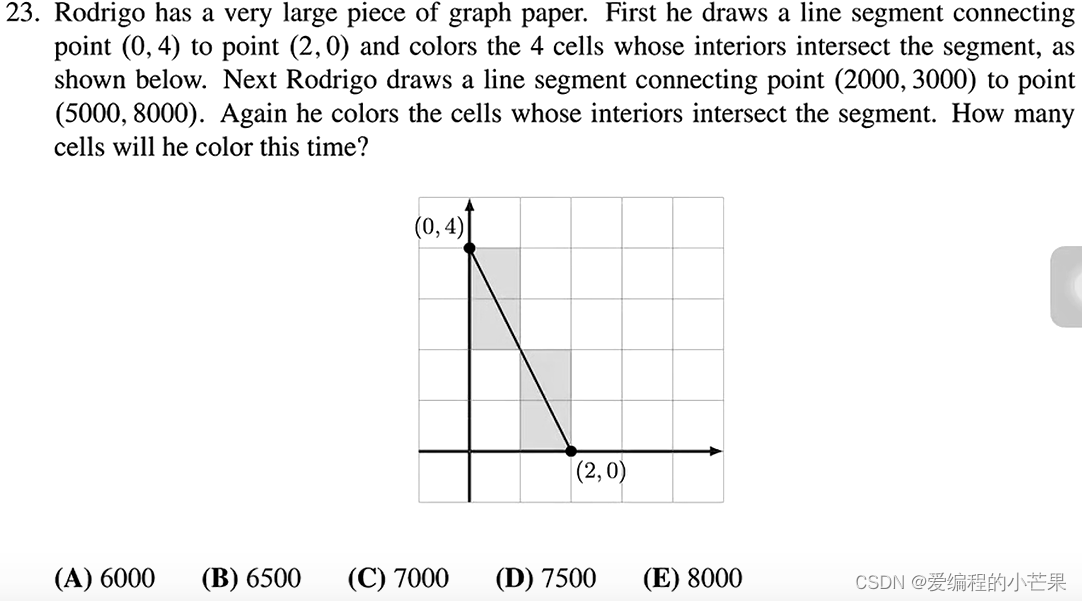
23.老题目，穿格子问题。

先算出长方形的长和宽：

长：8000-3000=5000

宽：5000-2000=3000

(5000/1000+3000/1000-1)*1000=7000

故选C

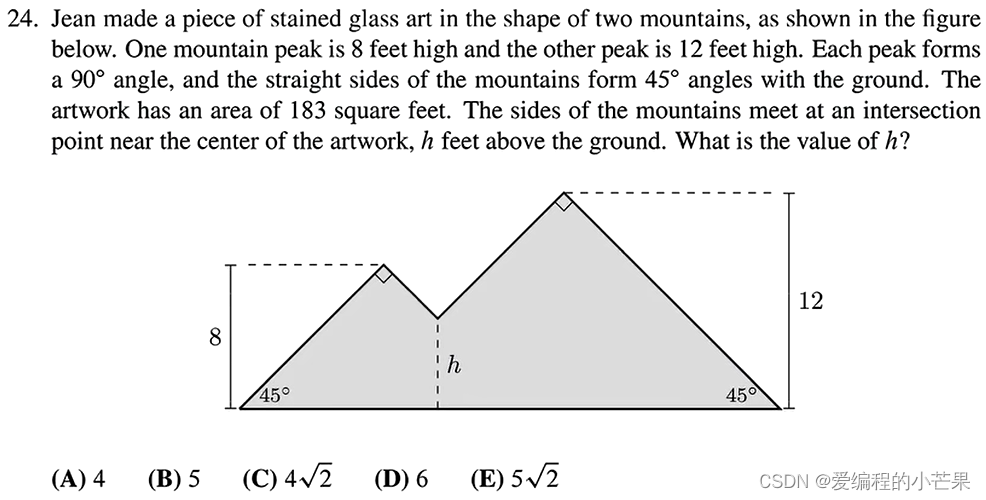
24.画图表数据。

先求出两个三角形不重合时的总面积：

8×8+12×12=208

重叠部分面积：

208-183=2 25=5×5

故选B

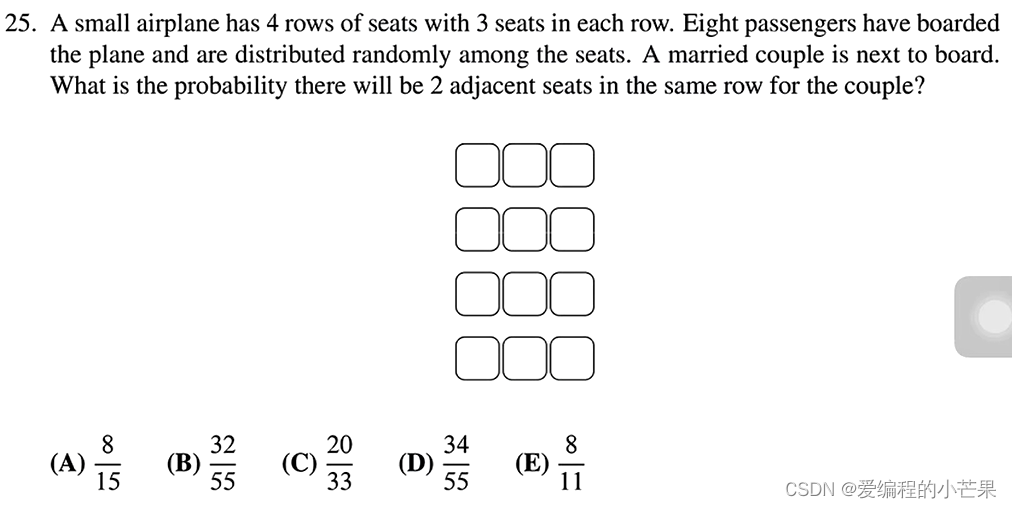
25.压轴题，分类讨论。

已经来了8名旅客，还有4个空位可以选，共 $C_{12}^{4}$ 种。

而满足夫妻相邻的座位分三种情况，每个加数表示每一行可以空的座位数：

3+1+0+0

2+2+0+0

2+1+1+0

第一种情况：有一行全部空出来，共有4种，剩下一个位置共有9种，4×9=36种。

第二种情况：四行任选两行，有 $C_{4}^{2}$ 种，每行有三种情况，但是一种不可以满足条件，故有3×3-1=8种。再乘上 $C_{4}^{2}$ =48种。

第三种情况：两个相邻位置有8种，剩下两个1有3×3×3种方法，共216种。

(36+48+216)÷495=300÷495=60÷99=20÷33

故选C