本文主要是介绍为了最大限度利用带宽,传输通道容量如何计算,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、结论:
传送通道容量 = 带宽 ✖️ 往返时延
二、过程:
1、传播时延和发送时延(带宽)通常决定一个报文的发送时间。
传输介质确定的时候,传播时延固定,发送时延根据数据报文的大小而不同。
①传播时延:
传播时延是指信号在传输媒体(例如电缆、光纤或空气)中传播所需的时间。它是从数据发送方发送信号到数据接收方接收到信号所经历的时间间隔。传播时延的大小取决于传输媒体的物理性质,主要由信号传播的速度和传播距离决定。
传播时延可以用以下公式表示:
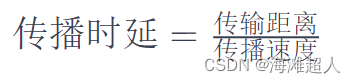
其中:
传输距离是信号在传输媒体中传播的距离。
传播速度是信号在传输媒体中的传播速度。
要注意的是,传播时延与数据的大小或传输速率无关,它主要受制于物理媒体的特性。因此,即使是很小的数据包也会有传播时延,这是由于信号在传输媒体中传播需要一定的时间。
②带宽:
带宽通常被归类为网络性能的一个重要参数,它与数据传输速率有关。带宽描述了网络连接在单位时间内能够传输的数据量,通常以位每秒(bps)为单位表示。
2、在传播速率慢的情况下,发送时延是主要因素。在传播速率快情况下(例如千兆比特速率下)传播时延是影响的主要因素。
eg:
假设有两个节点 A 和 B 之间的通信,它们之间的传播时延是10毫秒。如果在一个较慢的网络中,发送一个小数据报文到网络需要20毫秒,那么总延迟将主要由发送时延决定,即总延迟为 20 毫秒。
现在,如果在一个千兆比特的网络中,发送同样大小的数据报文到网络只需要1毫秒,那么总延迟将主要由传播时延决定,即总延迟为 10 毫秒。在这种情况下,发送时延相对较小,因为高速网络允许数据迅速传输到目的地。
3、为了最大限度利用带宽,发送方应该源源不断收到接收方发送的ack,对收到数据确认并更新滑动窗口大小。
4、传送通道容量计算方式:传送通道容量 = 带宽 ✖️ 往返时延。
开始阶段,通告的可用滑动窗口必须大于等与带宽和往返时延的乘积,才能确保在收到第一个ack前能够一直发送数据流量。因为发送第一个报文到收到的对应ack时间支付稍微RTT(客户端到服务端往返所化的时间)
RTT(Round-Trip Time)时间: RTT是指从发送数据到收到对应的确认所经过的时间,即数据从发送端传到接收端再返回的时间。RTT包含了传播延迟、处理延迟等。
带宽和往返时延的乘积: 带宽和往返时延的乘积反映了网络的传输能力。这个值表示在一个往返时延内,网络可以传输的最大比特数。表达式为:带宽 × RTT。
通告的可用滑动窗口: 指的是接收方通告给发送方的窗口大小,即接收方当前能够接受的未被确认的数据的最大数量。
eg:
假设有一个客户端(Sender)和一个服务器端(Receiver)之间进行TCP通信。客户端发送数据给服务器端,然后等待服务器端的确认。
带宽: 10 Mbps(10兆比特每秒)。
RTT: 50 毫秒(0.05 秒)。
计算带宽和往返时延的乘积:10 Mbps × 0.05 秒 = 0.5 Mb。
这意味着在一个往返时延内,网络最多可以传输0.5兆比特的数据。如果接收方通告的窗口大小小于0.5 Mb,那么发送方将不能充分利用网络的带宽,因为在一个往返时延内,网络无法传输更多的数据。因此,为了确保网络的充分利用,通告的可用滑动窗口大小应该大于等于带宽和往返时延的乘积。
这篇关于为了最大限度利用带宽,传输通道容量如何计算的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






