本文主要是介绍洛谷P2241统计方形,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目背景
1997年普及组第一题
题目描述
有一个n×m 方格的棋盘,求其方格包含多少正方形、长方形(不包含正方形)。
输入格式
一行,两个正整数 n,m(5000n≤5000,m≤5000)。
输出格式
一行,两个正整数,分别表示方格包含多少正方形、长方形(不包含正方形)。
输入输出样例
输入
2 3
输出
8 10
题目简单易懂,可是想要做这道题目还是需要一些小技巧的。
这里就拿题目的例子进行举例,有一个2 * 3的棋盘,求他的正方形个数和长方形个数
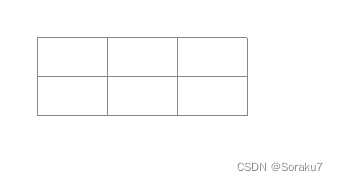
先看1 * 1的正方形个数 ,显然有6个 , 2 * 2的正方形总共有2个
再看长方形1 * 2的长方形有3个 , 2 * 1 的长方形个数有4个,1 * 3的长方形个数有2个,最后仅剩下一个大的长方形是2 * 3。
如果光是这样看,那么我们好像并不能找到什么规律 。现在我们需要找到一个能求出正方形长方形的规律 。这里是这样想的,我们带入一个坐标轴,求出每个点和正方形长方形的个数关系
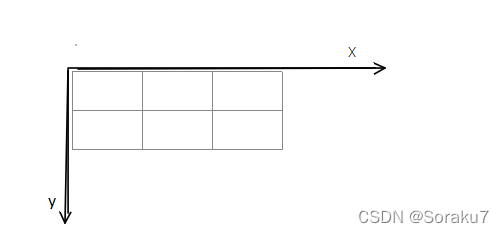
现在从(1 , 1)开始看起 , 正方形个数为1 , 长方形个数为0,总和为1
(2 , 1),此时相较于(1 , 1)比起来,正方形个数多了1 , 长方形个数多了1 , 总和多了2
(3 , 1),此时相较于(2 , 1)比起来,正方形个数多了1 , 长方形个数多了2 ,总和多了3
现在可以来总结一下规律 , 此规律如果有不了解的,或者是不太懂的可以自己根据我所推出的规律进行测试
正方形增加的个数应该为(x , y)坐标中较小的一个,而正方形和长方形所总共所增加的数应该为x * y。
看来有这样简单方便的规律 , 我们好像就可以算出棋盘中正方形的个数了。长方形的个数当然我们可以使用所有矩形的个数减去正方形的个数,自然就是长方形的个数了。
这里代码比较简单
#include<iostream>
#include<algorithm>
using namespace std;
int main() {long long n, m;long long squ = 0, sum = 0;cin >> n >> m;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {squ += min(i, j);sum = sum + i * j;}}cout << squ << " " << sum - squ;return 0;
}, 就不过多的进行注释了
这篇关于洛谷P2241统计方形的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






