决战排序之巅（二）

本文主要是介绍决战排序之巅（二），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

欢迎来到决战排序之巅栏目，
本期给大家带来的是归并排序与计数排序的实现与比较。
在上期决战排序之巅（一）中，给大家带来了插入排序(希尔) 与 选择排序(堆排) 的实现与比较，感兴趣的可以看看。

排序测试函数 void verify(int* arr, int n)

主要功能：测试arr数组中的顺序是否全为非升序的顺序。
代码如下：

void verify(int* arr, int n)
{for (int i = 1; i < n; i++){assert(arr[i] >= arr[i - 1]);}
}

如果arr数组中顺序不全为非升序，则assert()直接终止程序；
若全为非升序，则程序可通过该函数。

归并排序

基本思想：采用分治算法，将已有的有序子序列进行合并，得到完全有序的序列；即先使每个子序列有序，再使子序列所合并的序列有序。
归并排序的核心步骤就是：分解与合并。

递归方案

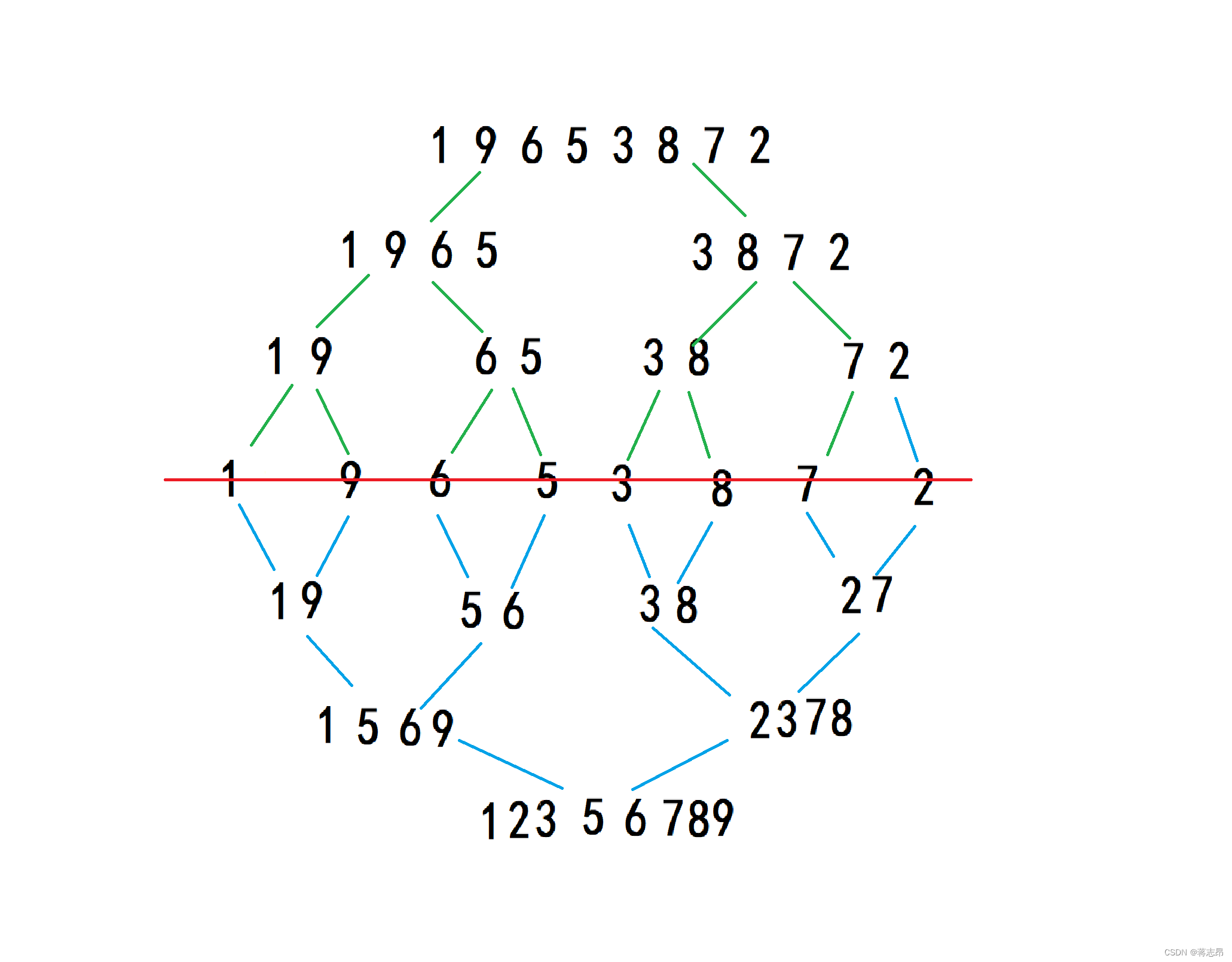
如下图所示：我们可以先将一组数据由大到小逐个分开，再依次合并。
下图绿线为分解，蓝线为合并。我们可以看到，排序数据分解时，当子序列内个数为1 时,不再分解；随后进行依次的合并，"1" "9" 合并为"1 9"的子序列，"5" "6"合并成"5 6"的体序列，同理可得"3 8" "2 7"，再让子序列合并，"1 9 6 5"合并成"1 5 6 9"。"3 8"和"2 7"合并成"2 3 7 8"。最后两个字序列合并成"1 2 3 5 6 7 8 9"
至此，归并排序完毕。

具体代码，如下：

void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);assert(tmp);_MergeSort(a, 0, n - 1, tmp);free(tmp);
}

void MergeSort(int* a, int n)是我们排序的调用函数，因为他的参数形式不宜用递归实现，所以我们可以写一个子函数void _MergeSort(int* a,int begin,int end ,int* tmp)来实现主要程序的编写，如下：

void _MergeSort(int* a,int begin,int end ,int* tmp)
{if (begin >= end)return;int mid = (begin + end) / 2;_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid+1, end, tmp);int left1 = begin, right1 = mid;int left2 = mid + 1, right2 = end;int i = 0;while (left1 <= right1 && left2 <= right2){if (a[left1] > a[left2])tmp[i++] = a[left2++];elsetmp[i++] = a[left1++];}while (left1 <= right1){tmp[i++] = a[left1++];}while (left2 <= right2){tmp[i++] = a[left2++];}memcpy(a + begin, tmp, i * sizeof(int));
}

我们先通过以下代码进行归并排序“分解”的实现

	if (begin >= end)return;	int mid = (begin + end) / 2;_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid+1, end, tmp);

当子序列内个数为1 时，return 返回；当子序列内个数大于1 时，进行以下编写：
有递归可知，此时的小标区间为[begin , mid] 与 [mid + 1 , end]是排好序的子区间，所有此时我们只要将其合并好就可以了。

	int left1 = begin, right1 = mid;int left2 = mid + 1, right2 = end;int i = 0;while (left1 <= right1 && left2 <= right2){if (a[left1] > a[left2])tmp[i++] = a[left2++];elsetmp[i++] = a[left1++];}while (left1 <= right1){tmp[i++] = a[left1++];}while (left2 <= right2){tmp[i++] = a[left2++];}memcpy(a + begin, tmp, i * sizeof(int));

最后将tmp上的数据拷贝到a的[begin , end]区间即可。

代码可行性测试

void _test()
{int n = 100000000;int* arr = (int*)malloc(sizeof(int) * n);for (int i = 0; i < n; i++){arr[i] = rand();}MergeSort(arr, n);verify(arr, n);free(arr);
}

运行结果如下 ：

程序通过verify(int* arr int n)函数,且成功运行，代码无误。

非递归方案

在非递归方案中我们可以利用循环来实现，主要实现过程如下视频所示：

我们可以定义一个gap并且gap的初始置为1，用来表示子序列的最小个数为1，随后在整体排完相邻两个子序列后，gap乘以2，此时数组内小标区间为$[n\ast gap,n\ast (gap\ast 2-1)]\cup [0,gap-1],n\in N^{+}$是有序的，如此循环直到,$n\le gap$时跳出循环，代码如下：

void MergeSortNonR(int* a,int n)
{int* tmp = (int*)malloc(sizeof(int) * n);assert(tmp);int gap = 1;while (n > gap){for (int i = 0; i < n; i += gap * 2){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + gap * 2 - 1;int j = begin1;if (end1 >= n && begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}while (begin1 <= end1){tmp[j++] = a[begin1++];}while (begin2 <= end2){tmp[j++] = a[begin2++];}memcpy( a + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}free(tmp);
}

我们先看如何分解，利用gap来确定子序列的元数个数，再利用for循环来实现两个相邻子序列的排序（即下标区间[begin1,end1] , [begin2,end2]的排序）
注意：在分配完区间[begin1,end1] ,和[begin2,end2]后，我们要对区间范围的有效性进行检查，因为非递归的方案通过比较相邻的子序列，gap以2的幂次方所增长，适用的数组长度也为2的幂次方，所以我们要对end1 , begin2 , end2进行检查，如果end1 , begin2 大于数组总个数n时，直接break即可，因为此时的[begin1，n-1]已经是有序的了；如果end2大于n则，令end2=n-1，此时我们只要排好[begin1,end2] , [begin2,n-1]即可,具体过程如下：

		for (int i = 0; i < n; i += gap * 2){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + gap * 2 - 1;int j = begin1;if (end1 >= n && begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}//合并过程}

合并过程与递归方案相同，但需要注意的是数组拷贝的时候，for循环依次拷贝一次。

代码可行性测试

程序通过verify(int* arr int n)函数,且成功运行，代码无误。

特点分析

特性：归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。
时间复杂度：O(N*logN)
空间复杂度：O(N)
稳定性：稳定

计数排序

基本思想：计数排序又称为鸽巢原理，是对哈希直接定址法的变形应用。

代码实现

实现步骤：

1. 选出要排序数组a中的最值，再相减求出数组的相对范围$n=max-min+1$
2. 用calloc开辟n个空间为tmp
3. 利用i遍历a，让数组tmp[$a[i]-min$]++
4. 最后，再遍历tmp , 此时tmp的数组下标 + min就表示数据的大小，tmp[数组下标]表示该数据的个数，所以在此时为a直接赋值即可。
   具体代码如下：

void CountSort(int* a, int n)
{int max = a[0], min = a[0];int i = 0;for (i = 0; i < n; i++){if (max < a[i]){max = a[i];}if (min > a[i]){min = a[i];}}int* tmp = (int*)calloc((max - min + 1), sizeof(int));assert(tmp);for (i = 0; i < n; i++){tmp[a[i] - min]++;}int j = 0;for (i = 0; i < max - min + 1; i++){int count = tmp[i];while (count--){a[j++] = i + min;}}free(tmp);
}

代码可行性测试

程序通过verify(int* arr int n)函数,且成功运行，代码无误。

特点分析

特点分析：计数排序在数据范围集中时，效率很高，但是适用范围及场景有限（例如：小数，结构体，字符串无法比较）
时间复杂度：O(MAX(N,范围))
空间复杂度：O(范围)

归并排序 VS 计数排序（Release版本）

说明

以下会分别对1w,10w,100w,1000w的数据进行100次的排序比较，并计算出排一趟的平均值。

下面是用来生成随机数的代码，可以确保正数与负数的随机分布。

	for (i = 0; i < n; i++){if (rand() % 2){arr3[i] = arr2[i] = arr1[i] = -rand() + i;}else{arr3[i] = arr2[i] = arr1[i] = rand() - i;}}

介绍就到这里了，让我们来看看这100次排序中，谁才是你心目中的排序呢？
PS：100次只是一个小小的测试数据，有兴趣的朋友可以在自己电脑上测试更多的来比较哦。

1w rand( ) 数据测试

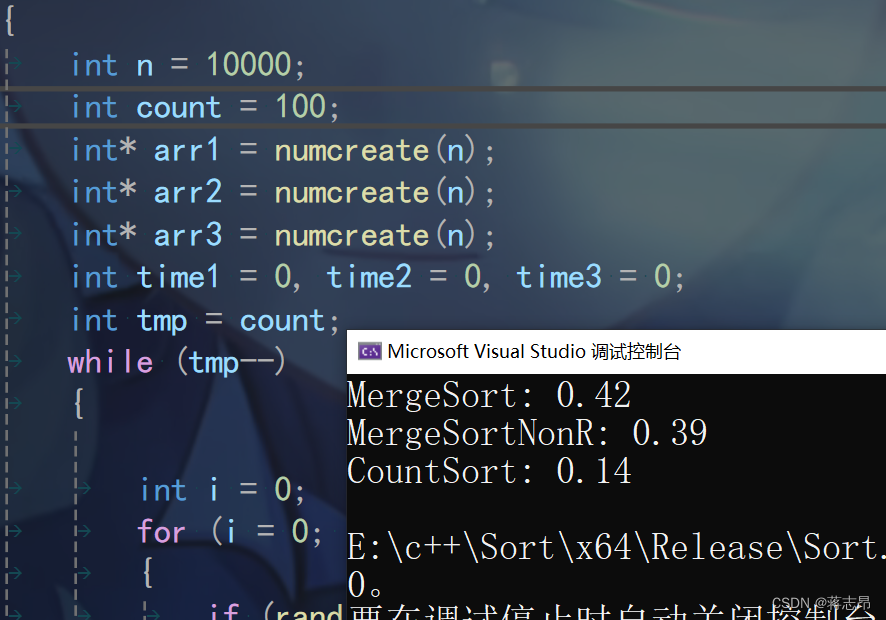
10w rand( ) 数据测试

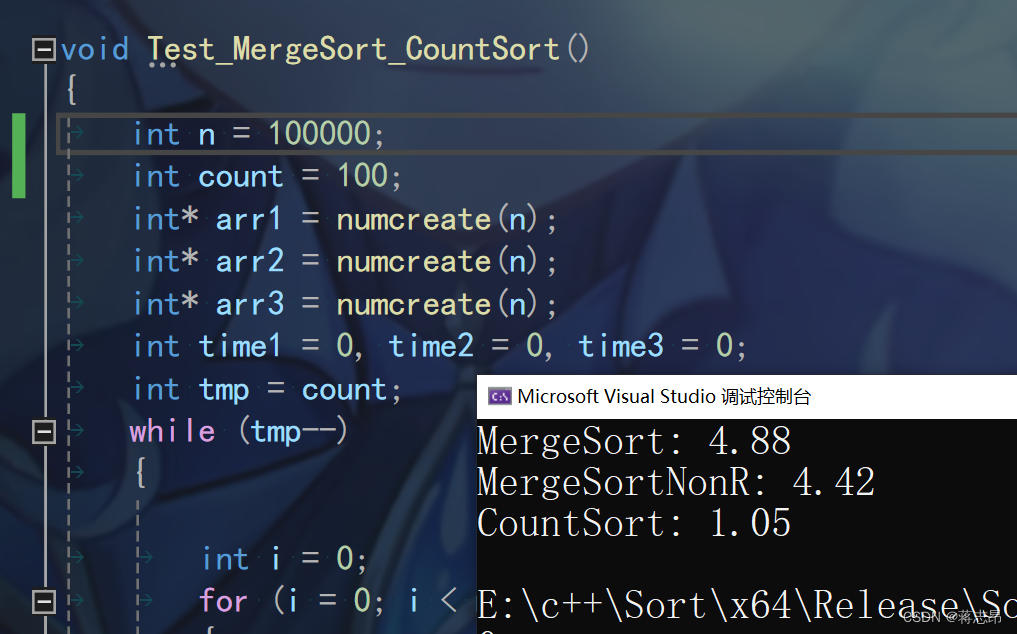
100w rand( ) 数据测试

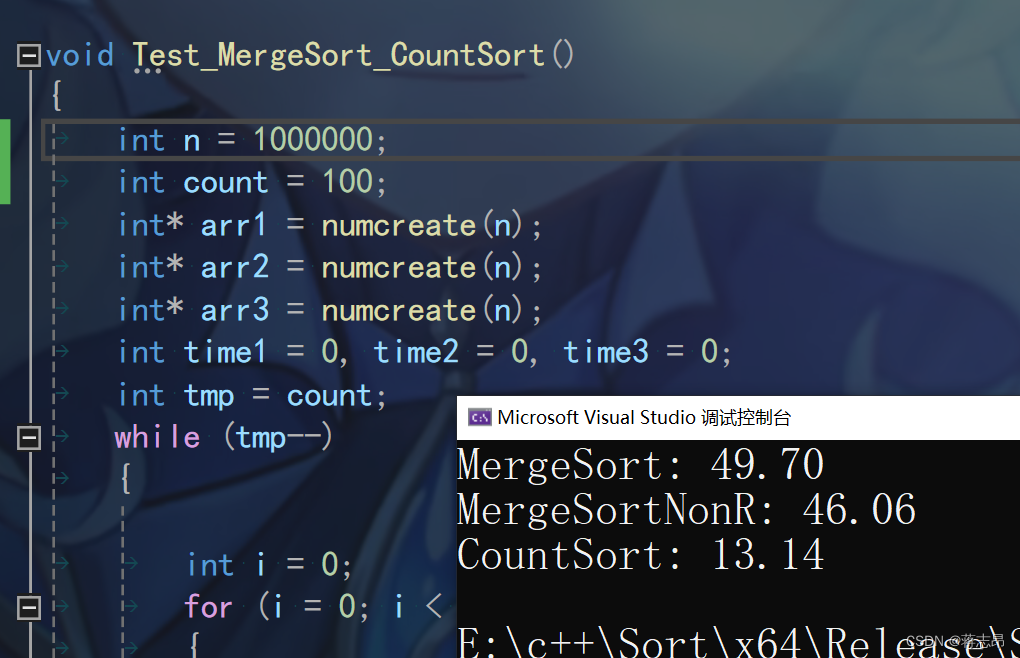
1000w rand( ) 数据测试

测试代码

void Test_MergeSort_CountSort()
{int n = 10000000;int count = 100;int* arr1 = numcreate(n);int* arr2 = numcreate(n);int* arr3 = numcreate(n);int time1 = 0, time2 = 0, time3 = 0;int tmp = count;while (tmp--){int i = 0;for (i = 0; i < n; i++){if (rand() % 2){arr3[i] = arr2[i] = arr1[i] = -rand() + i;}else{arr3[i] = arr2[i] = arr1[i] = rand() - i;}}int begin1 = clock();MergeSort(arr1, n);int end1 = clock();int begin2 = clock();MergeSortNonR(arr2, n);int end2 = clock();int begin3 = clock();CountSort(arr3, n);int end3 = clock();time1 += end1 - begin1;time2 += end2 - begin2;time3 += end3 - begin3;}printf("MergeSort: %.2f\n", (float)time1/count);printf("MergeSortNonR: %.2f\n", (float)time2 / count);printf("CountSort: %.2f\n", (float)time3 / count);free(arr1);free(arr2);free(arr3);
}

从结果来看，计数排序快于归并排序，但它的局限性无法比较小数，结构体与字符串；
再看归并排序，非递归类的要略胜一筹哦。

结语

看完之后，谁才是你心目中的排序呢？
欢迎留言，让我们一起来期待在下一期 《决战排序之巅(三)》。

以上就是本期的全部内容喜欢请多多关注吧！！！

这篇关于决战排序之巅（二）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---