本文主要是介绍二分入门总结 B - Cable master,C - Aggressive cows,A - Monthly Expense,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
二分入门
- A - Monthly Expense(最大值的最小值)
- 代码
- C - Aggressive cows(最小值的最大)
- 代码
- B - Cable master(只找最大的)
- 代码
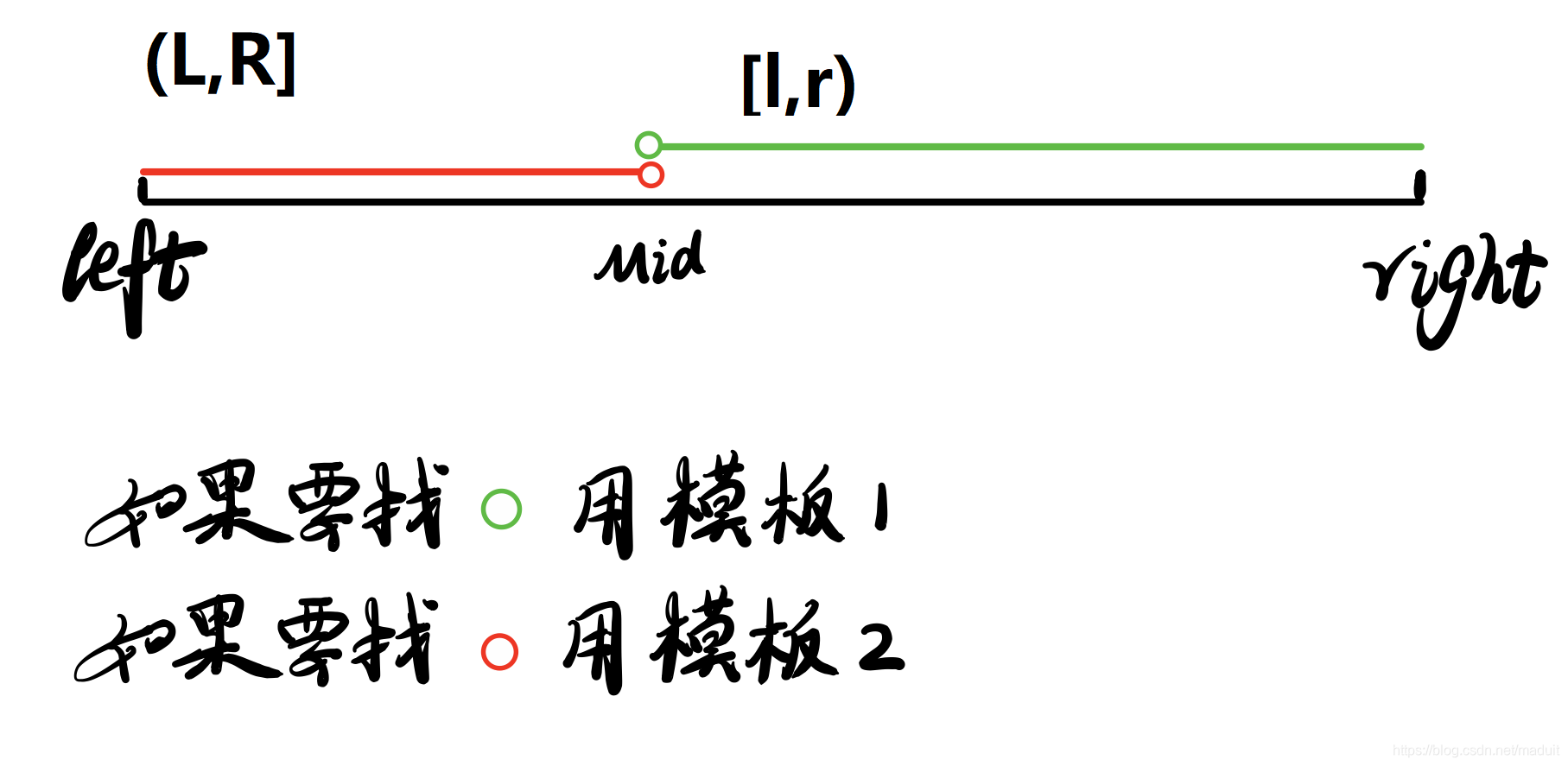
二分的模板有两种:
一种是:找大于等于给定数的第一个位置(满足条件的第一个数)
一种是:找小于等于给定数的最后一个数(满足条件的最后一个数字)
1.首先先引用一下大佬的图
链接:https://blog.csdn.net/yangyangcome/article/details/115979254
2.其次,看一下二分的模板。
https://blog.csdn.net/qq_43690454/article/details/104020240
**** 最小值的最大值
**** 最大值的最小值
求最小值最大化
二分区间(L,R]
bool check(int mid)
{
.......
}
L=0;//[L,R]的区间根据题目所定,
//这边写的区间都是下面题目的区间
R=a[n]-a[1];
二分模板
while(L<R)
{int mid=(l+r+1)>>1;if(check(mid)) l=mid;else r=mid-1;
}
求最大值最小化
二分区间[L,R)
bool check(int mid)
{
.......
}
L=max(.....); //[L,R]的区间根据题目所定,
//这边写的区间都是下面题目的区间
R=sum(.....);
二分模板
while(L<R)
{ll mid=l+r>>1;if(check(mid)) r=mid;else l=mid+1;
}
A - Monthly Expense(最大值的最小值)
题目:
Farmer John is an astounding accounting wizard and has realized he
might run out of money to run the farm. He has already calculated and
recorded the exact amount of money (1 ≤ moneyi ≤ 10,000) that he will
need to spend each day over the next N (1 ≤ N ≤ 100,000) days.FJ wants to create a budget for a sequential set of exactly M (1 ≤ M ≤
N) fiscal periods called “fajomonths”. Each of these fajomonths
contains a set of 1 or more consecutive days. Every day is contained
in exactly one fajomonth.FJ’s goal is to arrange the fajomonths so as to minimize the expenses
of the fajomonth with the highest spending and thus determine his
monthly spending limit. Input Line 1: Two space-separated integers: N
and M Lines 2…N+1: Line i+1 contains the number of dollars Farmer
John spends on the ith day Output Line 1: The smallest possible
monthly limit Farmer John can afford to live with.
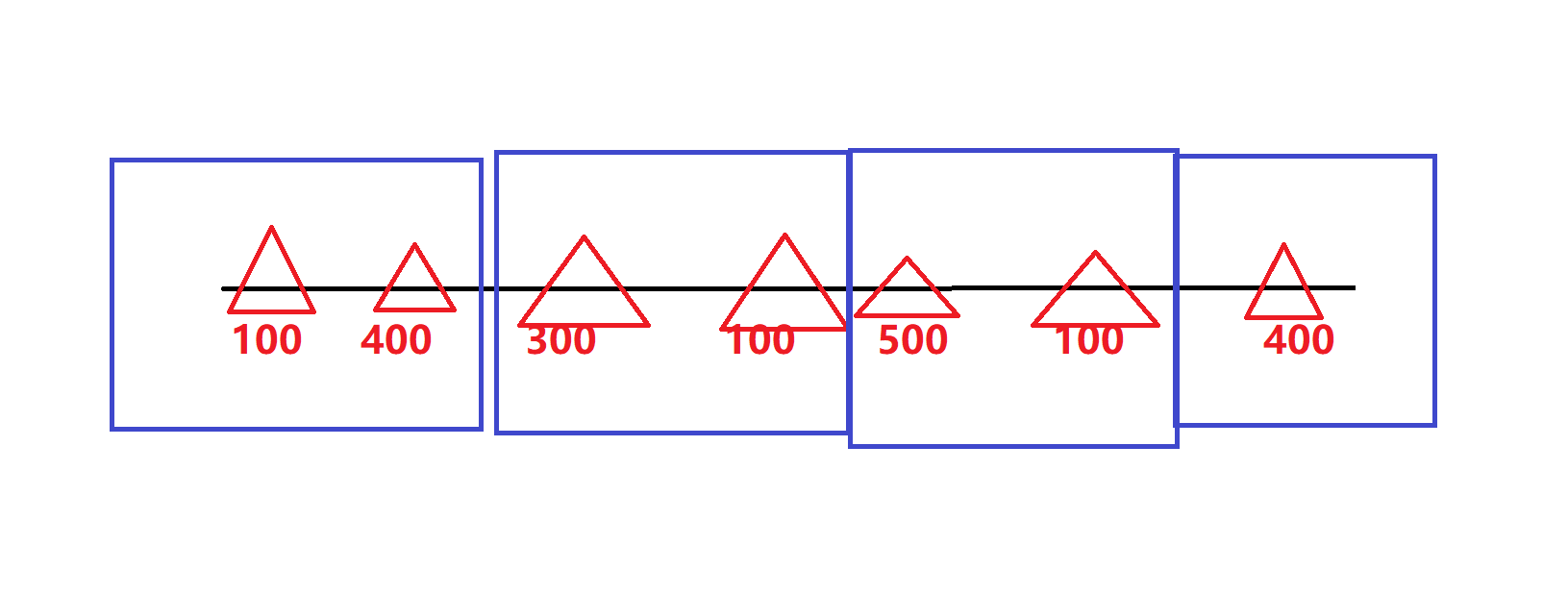
Sample Input
7 5
100
400
300
100
500
101
400
Sample Output
500
Hint
If Farmer John schedules the months so that the first two days are a month, the third and fourth are a month, and the last three are their own months, he spends at most $500 in any month. Any other method of scheduling gives a larger minimum monthly limit.
理解:
有个人,一共有N天,然后每天有一定的钱Money[i],然后一共有M个阶段时期,是一天,或者是连续几天,问周期花费最多的钱最小值是多少。实际就是一个最大值的最小化问题。
用最大值最小化模板
放个模板
求最大值最小化
二分区间[L,R)
bool check(int mid)
{
.......
}
L=max(.....); //[L,R]的区间根据题目所定,
//这边写的区间都是下面题目的区间
R=sum(.....);
二分模板
while(L<R)
{ll mid=l+r>>1;if(check(mid)) r=mid;else l=mid+1;
}
个人解题理解:
(找最大值的最小值)用图片上的绿色的部分

1.先统计sum总共给出的钱钱,最小的钱钱是给出钱钱的最大值。
(因为要找出给出天数划分的最大值的.最小.,那肯定是往大的开始找。)
2.开始二分。
3.check函数判断现在mid(二分中间值)的ans(划分天数)是否>=给定的m的天数。
4.如果>=成立,返回0(false),l=mid(左值右移动),说明现在范围(钱数)过小,组数过多,没找到最大钱数的范围,所以确定不了最大值的最小
5。else ,返回1,右值左移,说明现在的mid过于大,大到找不到符合分成m组的数,要缩小。
6.ans代表符合划分的个数,sum代表判断过的几天的花费钱总和。
7.此处mid指的是压缩总的区间(sum和给出最大钱钱中间值)
8.最后当 L不< R时退出循环。
9.找到图中的L,就是最大值中的第一个数(最小值)
10.输出的是最大
11.具体看代码注释吧。
代码
#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstdio>
#include<string>
#include<cstring>
using namespace std;
#define max 1000000
typedef long long ll;
ll n,m;
ll i;
ll a[max];bool check(ll mid)
{ll ans=0,sum=0; //ans是份数,sum是一份中的总钱数for(i=0;i<n;i++){if(sum+a[i]<=mid) //如果现在的sum+接下来给出的钱钱<=mid{sum+=a[i]; //那就继续加a[i]}else //如果现在sum+a[i]的>mid{sum=a[i]; //那就令现在的总钱钱sum=现在的a[i],//即接下来第一天的a[i]ans++; //组数++}}if(ans>=m) return 0; //如果组数>=m给出的分组数,//说明,mid虽然符合了要求,但还不是最大值/*这里的逻辑就是:mid值越小,那分的组数就越多*///所以,返回0,让区间范围的左值右移,增大一点else return 1; //这里else,说明ans组数<了m,那mid太大了,//需要把右边界向左移。
}
int main()
{while(cin>>n>>m){ll l=0,r=0,mid;memset(a,0,sizeof(a));for(i=0;i<n;i++){cin>>a[i];r=r+a[i]; //确定右边界if(l<a[i])l=a[i]; //确定左边界(给出值中的最大)}while(l<r) //当l<r不成立的时候,就是找到了mid(最大值区间){mid=(r+l)/2;if(check(mid)){r=mid;} elsel=mid+1;}cout<<l<<endl; //如图片所示,最大值的最小值是左边界值//所以输出l}return 0;
}
C - Aggressive cows(最小值的最大)
题目:
Farmer John has built a new long barn, with N (2 <= N <= 100,000) stalls. The stalls are located along a straight line at positions x1,…,xN (0 <= xi <= 1,000,000,000).
His C (2 <= C <= N) cows don’t like this barn layout and become aggressive towards each other once put into a stall. To prevent the cows from hurting each other, FJ want to assign the cows to the stalls, such that the minimum distance between any two of them is as large as possible. What is the largest minimum distance?
Input
Line 1: Two space-separated integers: N and C
Lines 2…N+1: Line i+1 contains an integer stall location, xi
Output
Line 1: One integer: the largest minimum distance
Sample Input
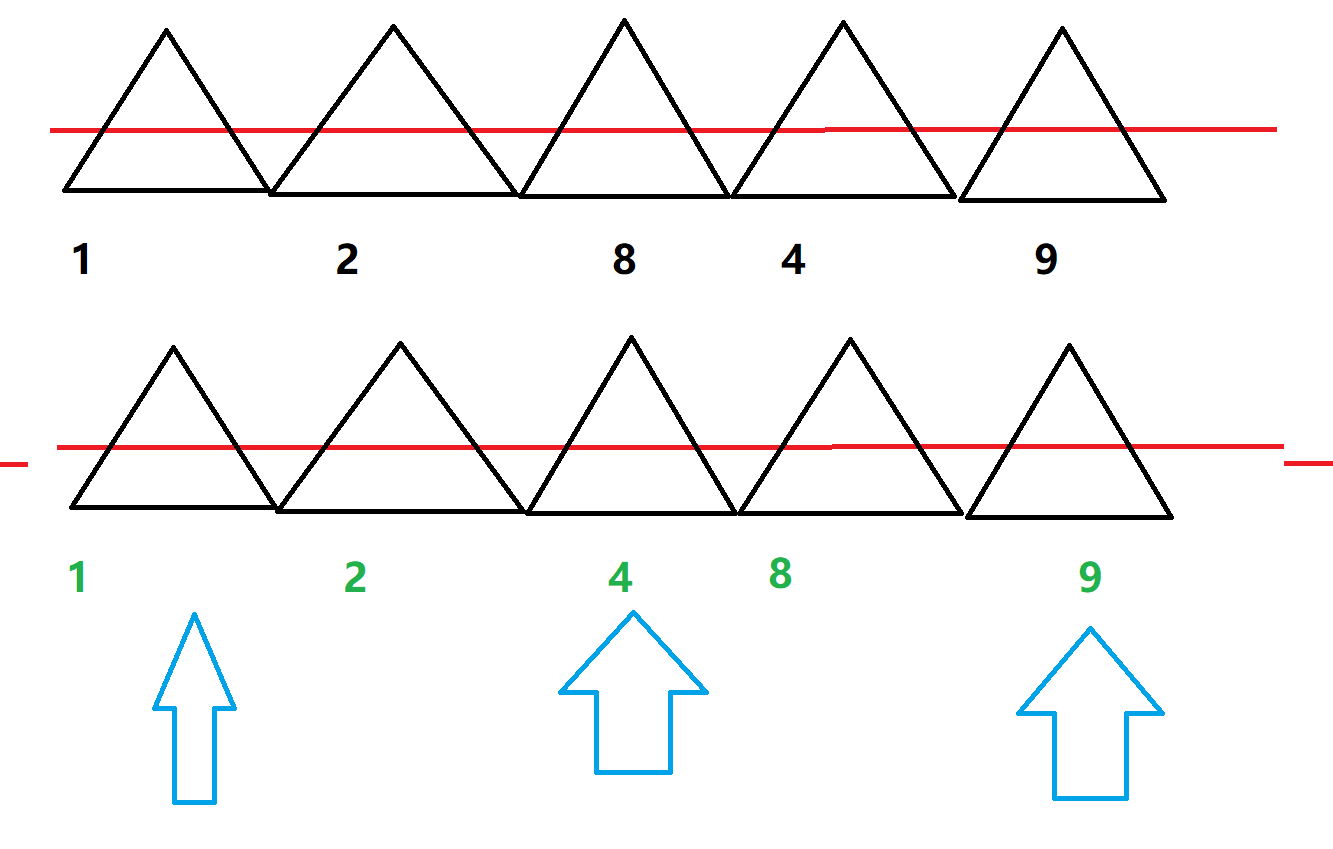
5 3
1
2
8
4
9
Sample Output
3
Hint
OUTPUT DETAILS:
FJ can put his 3 cows in the stalls at positions 1, 4 and 8, resulting in a minimum distance of 3.
Huge input data,scanf is recommended.
题目大致:
农夫 John 建造了一座很长的畜栏,它包括N (2≤N≤100,000)个隔间,
这些小隔间的位置为x 0 ,…,x N-1 (0≤x i ≤1,000,000,000,均为整数,各不相同). John的C(2≤C≤N)头牛每头分到一个隔间。牛都希望互相离得远点省得互相打扰。
怎样才能使任意两头牛之间的最小距离尽可能的大,这个最小的最大是多少呢? 用最小值最大的模板
放个模板
求最小值最大化
二分区间(L,R]
bool check(int mid)
{
.......
}
L=0;//[L,R]的区间根据题目所定,
//这边写的区间都是下面题目的区间
R=a[n-1]-a[0];
二分模板
while(L<R)
{int mid=(l+r+1)>>1;if(check(mid)) l=mid;else r=mid-1;
}
就是图中左边那一段。
个人理解:
1.既然是先找最小值,那肯定往小的里找,那左值为0,右值为最大的
2.先从小到大排序,然后开始二分
3.check函数判断现在的mid的sum是否>=c(sum指的是当前满足隔开奶牛数)(c指的是给出奶牛数)
4.如果>=c 成立,那返回1,左值右移,说明mid虽然符合条件,但是符合条件的sum(奶牛数)过多,说明隔间距离都太小,不存在最小里的最大,要向右找存在最小里最大的间隔。
5.else ,返回0,右值左移,说明mid(间隔)过大,找不到符合c奶牛的数量,要缩小间隔。
6.输出的是最小的最大间隔距离啊。
7.看代码吧。
代码
#include<cstdio>
#include<iostream>
#include<algorithm>
#define maxn 1000000
typedef long long ll;
using namespace std;
ll n,c;
ll a[maxn];
/*最小的最大*/
bool check(ll mid)
{ll ff=a[0]; //第一个隔间距离ll i;ll sum=1; //第一个奶牛一直在第一个,所以计数起点就是1for(i=1;i<n;i++){if(a[i]-ff>=mid) //当前间隔距离-前一个间隔距离是否>=mid//成立的话{sum++; //奶牛数加+1 ff=a[i]; // 前一个间隔距离更新为a[i]}}if(sum>=c) return 1; //奶牛数>=给出的奶牛数else return 0; //小于
}
int main()
{cin>>n>>c;ll i;for(i=0;i<n;i++){cin>>a[i];}sort(a,a+n); //排序,依次找间隔ll mid; ll l=0,r=a[n-1]-a[0];//找左值和右值
while(l<r) //当l<r不成立的时候,就是找到了符合奶牛数的最大间隔距离{int mid=(l+r+1)>>1; if(check(mid)) l=mid; else r=mid-1;}cout<<r<<endl; //如图,取右值。return 0;
}
B - Cable master(只找最大的)
题目:
Inhabitants of the Wonderland have decided to hold a regional programming contest. The Judging Committee has volunteered and has promised to organize the most honest contest ever. It was decided to connect computers for the contestants using a “star” topology - i.e. connect them all to a single central hub. To organize a truly honest contest, the Head of the Judging Committee has decreed to place all contestants evenly around the hub on an equal distance from it.
To buy network cables, the Judging Committee has contacted a local network solutions provider with a request to sell for them a specified number of cables with equal lengths. The Judging Committee wants the cables to be as long as possible to sit contestants as far from each other as possible.
The Cable Master of the company was assigned to the task. He knows the length of each cable in the stock up to a centimeter,and he can cut them with a centimeter precision being told the length of the pieces he must cut. However, this time, the length is not known and the Cable Master is completely puzzled.
You are to help the Cable Master, by writing a program that will determine the maximal possible length of a cable piece that can be cut from the cables in the stock, to get the specified number of pieces.
Input
The first line of the input file contains two integer numb ers N and K, separated by a space. N (1 = N = 10000) is the number of cables in the stock, and K (1 = K = 10000) is the number of requested pieces. The first line is followed by N lines with one number per line, that specify the length of each cable in the stock in meters. All cables are at least 1 meter and at most 100 kilometers in length. All lengths in the input file are written with a centimeter precision, with exactly two digits after a decimal point.
Output
Write to the output file the maximal length (in meters) of the pieces that Cable Master may cut from the cables in the stock to get the requested number of pieces. The number must be written with a centimeter precision, with exactly two digits after a decimal point.
If it is not possible to cut the requested number of pieces each one being at least one centimeter long, then the output file must contain the single number “0.00” (without quotes).
Sample Input
4 11
8.02
7.43
4.57
5.39
Sample Output
2.00
理解:
对于给定的几条电缆(位于仓库中),相互不可以拼接,而要截取出给定段数下最长的电缆
如果能够获得合理的长度(>0),那么输出即可,如果不可以则输出0二分治问题,需要对于所有的电缆遍历处理,以方便判断特定长度能否裁出符合条件的电缆条数。如果是不可拼接(如题意的情况),二分点的右端点取到最长的一条电缆即可(假设是可以拼接的电缆,那么拼接起来之后求即可)
P.S:
必须从最大最长的那条电缆开始二分。当然不可以从最小的最短的那一条开始二分,如果最短的电缆作为右端点,假设存在所需电缆条数小于仓库电缆条数的情况,那么答案必定会比求得的答案更大,还有其他一些问题等等。
代码
#include<iostream>
#define maxn 1e8
using namespace std;int n,m;double a[100010];
/*有n根电线,要分成m段,问能分成m段的最大的长度是多少?*/
bool check(double mid)
{int ans=0; //电线段数int i;for(i=1;i<=n;i++)ans=ans+(int)(a[i]/mid); //每一根分的段数相加if(ans>=m) return 1; //总段数>=给出段数那就1,左值右移,说明给出的每段距离太小else return 0; //段数少了,每段长度过大,右值左移,缩小长度
}
int main()
{cin>>n>>m;int i;double sum=0.0;for(i=1;i<=n;i++){cin>>a[i];sum=sum+a[i]; //所有电线总长}double mid,l=0.0,r=sum/m; //右值是能分的平均长度while (r-l>1e-5){mid=(r+l)/2;if(check(mid)){l=mid; }else{r=mid;} }printf("%.2f\n",(int)(r*100)/100.0); //既然找最大那就肯定是右值呗,看图return 0;
}这篇关于二分入门总结 B - Cable master,C - Aggressive cows,A - Monthly Expense的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!