本文主要是介绍【Codeforces Round 364 (Div 2)E】【树上路径 贪心】Connecting Universities 树上2k个点配对使得路径之和尽可能大,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Treeland is a country in which there are n towns connected by n - 1 two-way road such that it's possible to get from any town to any other town.
In Treeland there are 2k universities which are located in different towns.
Recently, the president signed the decree to connect universities by high-speed network.The Ministry of Education understood the decree in its own way and decided that it was enough to connect each university with another one by using a cable. Formally, the decree will be done!
To have the maximum sum in the budget, the Ministry decided to divide universities into pairs so that the total length of the required cable will be maximum. In other words, the total distance between universities in k pairs should be as large as possible.
Help the Ministry to find the maximum total distance. Of course, each university should be present in only one pair. Consider that all roads have the same length which is equal to 1.
The first line of the input contains two integers n and k (2 ≤ n ≤ 200 000, 1 ≤ k ≤ n / 2) — the number of towns in Treeland and the number of university pairs. Consider that towns are numbered from 1 to n.
The second line contains 2k distinct integers u1, u2, ..., u2k (1 ≤ ui ≤ n) — indices of towns in which universities are located.
The next n - 1 line contains the description of roads. Each line contains the pair of integers xj and yj (1 ≤ xj, yj ≤ n), which means that the j-th road connects towns xj and yj. All of them are two-way roads. You can move from any town to any other using only these roads.
Print the maximum possible sum of distances in the division of universities into k pairs.
7 2 1 5 6 2 1 3 3 2 4 5 3 7 4 3 4 6
6
9 3 3 2 1 6 5 9 8 9 3 2 2 7 3 4 7 6 4 5 2 1 2 8
9
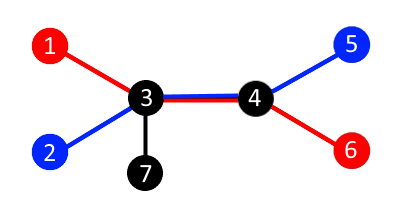
The figure below shows one of possible division into pairs in the first test. If you connect universities number 1 and 6 (marked in red) and universities number 2 and 5 (marked in blue) by using the cable, the total distance will equal 6 which will be the maximum sum in this example.
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<string>
#include<ctype.h>
#include<math.h>
#include<set>
#include<map>
#include<vector>
#include<queue>
#include<bitset>
#include<algorithm>
#include<time.h>
using namespace std;
void fre() { freopen("c://test//input.in", "r", stdin); freopen("c://test//output.out", "w", stdout); }
#define MS(x,y) memset(x,y,sizeof(x))
#define MC(x,y) memcpy(x,y,sizeof(x))
#define MP(x,y) make_pair(x,y)
#define ls o<<1
#define rs o<<1|1
typedef long long LL;
typedef unsigned long long UL;
typedef unsigned int UI;
template <class T1, class T2>inline void gmax(T1 &a, T2 b) { if (b>a)a = b; }
template <class T1, class T2>inline void gmin(T1 &a, T2 b) { if (b<a)a = b; }
const int N = 2e5+10, M = 0, Z = 1e9 + 7, ms63 = 0x3f3f3f3f;
int n, k;
int e[N];
vector<int>a[N];
LL ans;
void dfs(int x, int fa)
{for (int i = a[x].size() - 1; ~i; --i){int y = a[x][i];if (y == fa)continue;dfs(y, x);ans += min(e[y], k * 2 - e[y]);e[x] += e[y];}
}
int main()
{while (~scanf("%d%d", &n, &k)){for (int i = 1; i <= n; ++i)a[i].clear(), e[i] = 0;for (int i = 1; i <= k * 2; ++i){int x; scanf("%d", &x);e[x] = 1;}for (int i = 1; i < n; ++i){int x, y;scanf("%d%d", &x, &y);a[x].push_back(y);a[y].push_back(x);}ans = 0;dfs(1, 0);printf("%lld\n", ans);}return 0;
}
/*
【trick&&吐槽】
CF涨了好多分,原因就是因为胆子大233【题意】
给你一棵树,树上n(2e5)个点,树边权值都认定为1.
其中有2k(2k<=n)个点为特殊点。
我们希望在2k个特殊点中,搭配出k对点。
然后使得这k对点所形成的路径的权值之和尽可能大。
输出这个最大路径权值【类型】
贪心 贡献式思维【分析】
这道题被我很快产生了一种猜想。
这种猜想是基于"贡献式思维"展开的。
就是——
每条边最多会被多少条路径选中呢?
显然是——
min(这条边一侧的点数,这条边另外一侧的点数)
于是我这样几分钟写完,就AC掉了。显然,刚才求出了答案的可能最大值。
那么这个最大值是否一定能够取到呢?
我们粗略证明一下——
显然,每个点为根的子树,每个内部的点如果能向外连,肯定向外连更优,而且这个很容易做到。
然后,问题慢慢地有些显露出"重心"的性质和意义来。
重心把这棵树分成了若干块,每块的节点数都不超过2/k显然我们肯定把每一块和非该块的节点连边。
这样所得到的答案,正好与一开始的贡献算法得到的答案相符合。
而且更直观地看出问题的合法性。【时间复杂度&&优化】
O(n)*/这篇关于【Codeforces Round 364 (Div 2)E】【树上路径 贪心】Connecting Universities 树上2k个点配对使得路径之和尽可能大的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






