本文主要是介绍利用Monte Carlo进行数值积分(二),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
进步空间很大的算法版本
话说去年6月的一个周六,我很无聊地发了一个帖子,写了一个自己感觉有点无聊的帖子。
Matlab多重积分的两种实现【从六重积分到一百重积分】![]() https://withstand.blog.csdn.net/article/details/127564478
https://withstand.blog.csdn.net/article/details/127564478
这个帖子居然成了我这种懒人随性瞎写的博文中阅读量、收藏量和评论量最多的一个。
很多人对我不写说明,不写例子提出了意见,开头我写的那个代码里面还有一个小问题。
时隔7个月之后,我抽出一点时间来看这个算法,发现问题简直是大大的。
function ret = integral6mc(fun, lb, ub, N)% fun是被积分的函数% lb和ub是积分变量的范围,每个都是六维数组% N MC采样的数目,一般取个几千、几万试一下差不多就行V = prod(abs(ub-lb)); % 计算超立方体的体积,向量化计算每一个维度的长度(绝对值),求所有维度的乘积n = length(lb); % 维数sample = (ub-lb) .* rand(N, n) + repmat(lb,N,1); %产生一个Nxn的随机数组,然后转换到lb~ub的范围,repmat函数是复制矩阵,把行向量复制程Nxnsample_arguments = num2cell(sample, 1);% 把上面的Nxn矩阵换成按列排列的cell(n个元素)results = cell2mat(arrayfun(fun, sample_arguments{:}, 'UniformOutput', 0));%调用被积函数,被积函数的参数有n个,把cell展开({:}操作),这里arrayfun得到的是cell,再合并成mat,就是N个结果的向量ret = sum(results) * V / N; % 这是MC的核心算法,乘以体积除以样本数丑陋的'UniformOutput'以及为什么
首先,这里很无聊的搞了cell2mat,以及'UniformOutput', 0的参数,都是因为没仔细考虑,瞎写的。
这里的核心问题是什么呢?是arrayfun这个函数。
这个函数和并行比如parfor这些没关系,是一个单线程的函数,就是把第一个参数(一个函数句柄)逐次应用到后续参数的每一个对应的元素上去。
这里其实有一个小小的问题,是一位强迫我写一个例子的网友提出来的,很对。
f = @(x, y) x * y这个函数有两个参数,我们可以看到,如果x和y都是标量(一个数字),这个函数没啥问题。如果x,y是两个size一样的向量或者矩阵或者高维矩阵,那么他计算的就不是简单的乘法。只所以我前面调用arrayfun的过程中,需要设置输出可能不一致,就是因为我的目标函数没有写按元操作。
在采用arrayfun的时候,我们应该给出如此的约束, 目标函数是一个按元操作的函数,也就是,上面的函数应该写成:
f = @(x, y) x .* y这个问题在我原来用的matlab版本中貌似是个问题,但是今天我更新了matlab,看起来没啥问题了,那种写法都是可以的,最终的计算时间也是相当的,看起来就是arrayfun的内部没有做任何向量化的计算。这个实际上很奇怪,我感觉应该是优化到采用向量化的cpu指令来计算会比较合理……
更好的版本
在这个条件下,我们的mc函数就能够写成:
function ret = mci(fun, lb, ub, N)% fun是被积分的函数% lb和ub是积分变量的范围,每个都是六维数组% N MC采样的数目,一般取个几千、几万试一下差不多就行V = prod(abs(ub-lb)); % 计算超立方体的体积,向量化计算每一个维度的长度(绝对值),求所有维度的乘积n = length(lb); % 维数sample = (ub-lb) .* rand(N, n) + repmat(lb,N,1); %产生一个Nxn的随机数组,然后转换到lb~ub的范围,repmat函数是复制矩阵,把行向量复制程Nxnsample_arguments = num2cell(sample, 1);% 把上面的Nxn矩阵换成按列排列的cell(n个元素)results = arrayfun(fun, sample_arguments{:});ret = sum(results) * V / N; % 这是MC的核心算法,乘以体积除以样本数这里依然有同样的问题,就是num2cell,这个部分利用matlab把函数的多个参数当成cell的调用惯例,也可以写成:
function ret = mci(fun, lb, ub, N)% fun是被积分的函数% lb和ub是积分变量的范围,每个都是六维数组% N MC采样的数目,一般取个几千、几万试一下差不多就行V = prod(abs(ub-lb)); % 计算超立方体的体积,向量化计算每一个维度的长度(绝对值),求所有维度的乘积n = length(lb); % 维数sample = (ub-lb) .* rand(N, n) + repmat(lb,N,1); %产生一个Nxn的随机数组,然后转换到lb~ub的范围,repmat函数是复制矩阵,把行向量复制程Nxnsample_arguments = cell(n, 1);for i = 1:nsample_arguments{i} = sample(:,i);endresults = arrayfun(fun, sample_arguments{:});ret = sum(results) * V / N; % 这是MC的核心算法,乘以体积除以样本数这两个函数是一毛一样的,用for循环和用num2cell带来的差别微乎其微。
一点点例子以及profile
一维的无聊例子
先搞一个一点也不excited的例子。
定积分
如果a=0, b=1,积分结果为0.5。
f = @(x) x;n = round(logspace(2, 6, 50)); //必须保证是整数results = arrayfun(@(N)mci(f, lb, ub, N), n);figuresemilogx(n, results, 'x');hold onsemilogx([100, 1e6], [0.5, 0.5])xlabel("N");ylabel("\int_0^1 x dx")print -dpng -r300 convergencefigureloglog(n, abs(results-0.5), '+')xlabel("N")ylabel("\sigma")print -dpng -r300 sigma收敛的结果如图:

误差的loglog图:
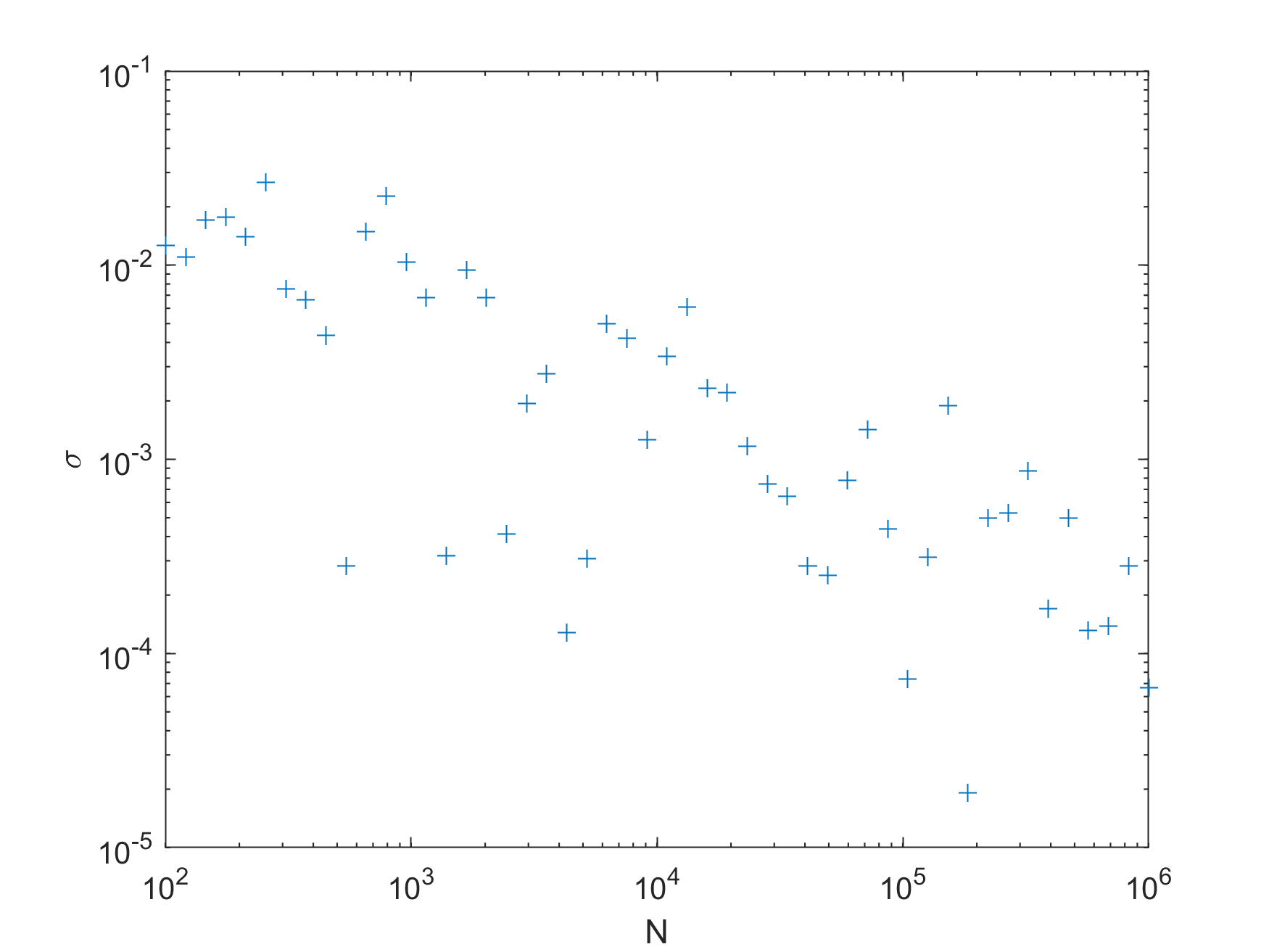
二维的略微不那么无聊例子
下面还一点点稍微不无聊一点的。
积分:
积分代码:
f = @(x,y) x * y;n = round(logspace(2, 6, 50)); //必须保证是整数results = arrayfun(@(N)mci(f, lb, ub, N), n);figuresemilogx(n, results, 'x');hold onsemilogx([100, 1e6], [0.25, 0.25])xlabel("N");ylabel("\int_0^1\int_0^1 x y dx dy")print -dpng -r300 convergencefigureloglog(n, abs(results-0.25), '+')xlabel("N")ylabel("\sigma")print -dpng -r300 sigma收敛速度:

误差结果:
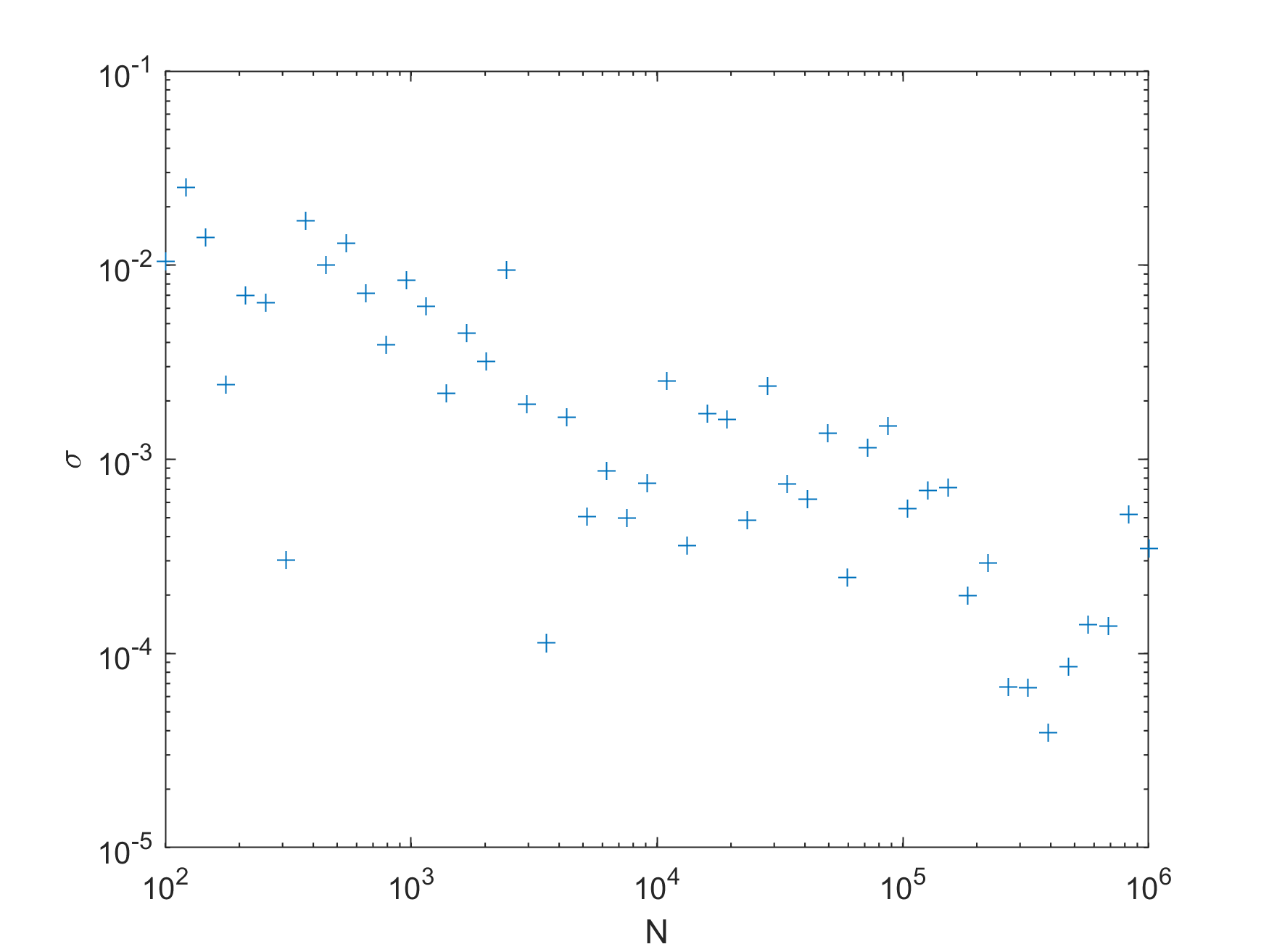
2维的情况下很快就收敛到3位小数(10000次采样)。
100维的例子
我们弄一个100维的简单函数.
在区间积分的真值是
。
对应的代码:
function ret = fn(varargin)n = length(varargin);vars = zeros(n, 1);for i=1:nvars(i) = varargin{i};endret = sum(vars .^ 2);对应的收敛性代码。
N = 100;true_value = N * 1.0 / 3.0;lb = zeros(1, N); %这里必须是1 * N, 而不是N * 1ub = ones(1, N);n = round(logspace(2, 6, 50));results = arrayfun(@(N)mci(@fn, lb, ub, N), n);figuresemilogx(n, results, 'x');hold onsemilogx([100, 1e6], [true_value, true_value])xlabel("N");ylabel("\int f")print -dpng -r300 convergencefigureloglog(n, abs(results-true_value), '+')xlabel("N")ylabel("\sigma")print -dpng -r300 delta可以看到蒙特卡洛方法有一个很好很好的特性,就是积分函数的维数跟算法复杂度完全没有关系。就算是100维,一样给它弄到三位有效数字的积分结果。
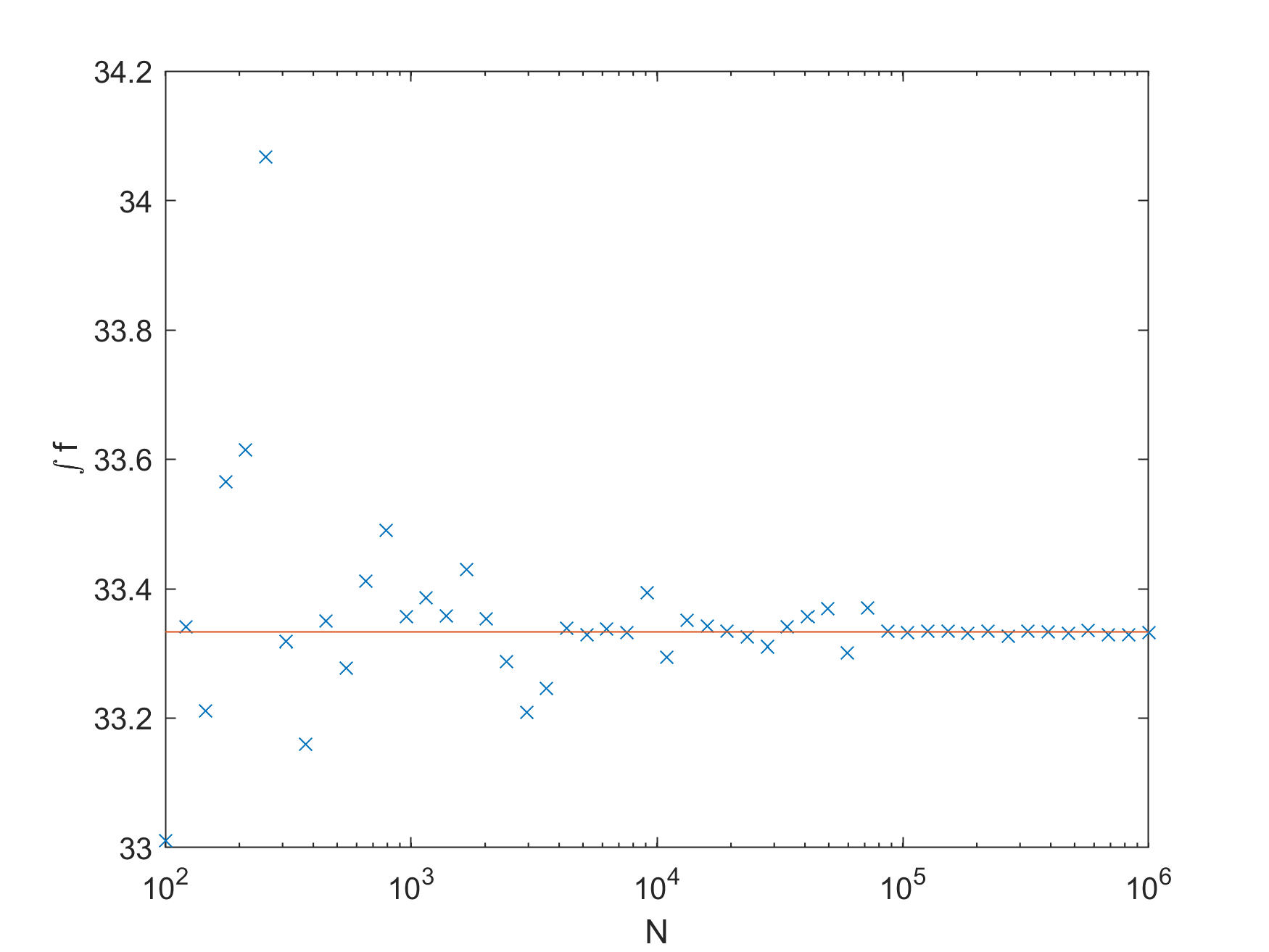

算法的典型时间特性
这个函数中一半的时间都在调用fn函数,这个函数一点也不美……
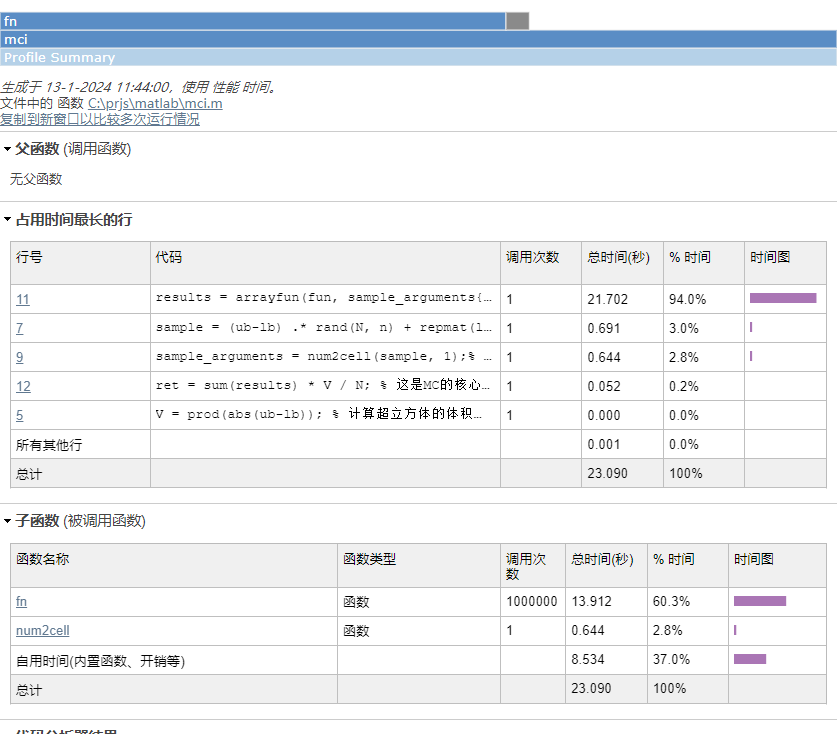
好吧,看起来100层并没有什么,也不需要那么多考虑。
GPU版本
当然,我还很无聊地写了一个gpu版本,效果简直是碉堡了。
这里就不多说,上个代码就算了。
function ret = mci_gpu(fun, lb, ub, N)% fun是被积分的函数% lb和ub是积分变量的范围,每个都是六维数组% N MC采样的数目,一般取个几千、几万试一下差不多就行V = prod(abs(ub-lb)); % 计算超立方体的体积,向量化计算每一个维度的长度(绝对值),求所有维度的乘积n = length(lb); % 维数sample = (ub-lb) .* rand(N, n, 'gpuArray') + repmat(lb,N,1); %产生一个Nxn的随机数组,然后转换到lb~ub的范围,repmat函数是复制矩阵,把行向量复制程Nxnargs = cell(n, 1);for i = 1:nargs{i} = sample(:,i);endresults = arrayfun(fun, args{:});%调用被积函数ret = gather(sum(results) * V / N); % 这是MC的核心算法,乘以体积除以样本数调用的方法跟前面那个函数一样,就是有一个问题,在gpu中计算时,不能调用100维的那个函数,因为要使用动态输入参数个数。
gpu版本的唯一不同就是把数组创建在显存中,最终这个计算里面最花时间的就是创建数组,实际的arrayfun的时间基本可以忽略,也是一个挺有意思的事情。最终用gather函数把结果从显存中取出来。
一点都不想参考的参考文献
[1] 张艳. 利用蒙特卡罗方法求解数值积分[J]. 高等数学研究, 2023, 26(1): 44-46+61.
这篇关于利用Monte Carlo进行数值积分(二)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




