本文主要是介绍机器学习-波士顿房价预测,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一.数据处理
读入数据
数据形状变换
数据集划分
数据归一化处理
将上面封装成load data函数
二. 模型设计
完整封装运行代码:
根据loss值进行梯度计算
控制部分变量的变化图像:
一.数据处理
读入数据
# 导入需要用到的package
import numpy as np
import json
# 读入训练数据
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ')//这个函数用于从文件
datafile中读取数据。它将文件中的数据按照给定的分隔符sep=' '进行分割,并将分割后的数据加载到一个 NumPy 数组中。
数据形状变换
# 读入之后的数据被转化成1维array,其中array的第0-13项是第一条数据,第14-27项是第二条数据,以此类推.... # 这里对原始数据做reshape,变成N x 14的形式 feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ] feature_num = len(feature_names) data = data.reshape([data.shape[0] // feature_num, feature_num])//data.shape[0]返回数据矩阵data的行数,而feature_num代表每个样本的特征数。通过将数据矩阵的总行数除以特征数,可以得到样本的数量。然后将矩阵data重塑为新的形状,其中每行包含feature_num个特征。 //data原本是个以空格分割的一维数组,现在变成了一个data.shape[0] // feature_num个行,feature_num个列的二位数组 形如:// 样本1的特征0 样本1的特征1 ...样本1的特征m// 样本2的特征0 ...// 样本3的特征0 ......// 样本N的特征0 ...
注:
x = data[0]//含义:第一个样本的所有数据,data数组的第一行
print(x.shape)
print(x)/*(14,)
[6.320e-03 1.800e+01 2.310e+00 0.000e+00 5.380e-01 6.575e+00 6.520e+014.090e+00 1.000e+00 2.960e+02 1.530e+01 3.969e+02 4.980e+00 2.400e+01]*/数据集划分
ratio = 0.8 offset = int(data.shape[0] * ratio) training_data = data[:offset]/*首先,根据给定的ratio比例,计算出划分点的位置(offset),即将数据矩阵按照比例划分为两部分。然后,通过使用切片操作(data[:offset]),将原始数据(data)的前offset行作为训练数据(training_data)。因此,这两行代码的作用是将data矩阵的前ratio比例的数据划分为训练数据集,并将其赋值给training_data。*/training_data.shape//(404, 14)
数据归一化处理
对每个特征进行归一化处理,使得每个特征的取值缩放到0~1之间。这样做有两个好处:一是模型训练更高效,在本节的后半部分会详细说明;二是特征前的权重大小可以代表该变量对预测结果的贡献度(因为每个特征值本身的范围相同)
# 计算train数据集的最大值,最小值 maximums, minimums = \training_data.max(axis=0), \training_data.min(axis=0) //通过使用max和min函数来计算训练数据集每个特征的最大值和最小值。axis=0表示沿着列的方向进行计算。# 对数据进行归一化处理 for i in range(feature_num):data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i]) //data[:, i]表示选取数据集中的第i个特征 //首先,通过减去最小值,将数据转化为相对范围。然后,除以最大值和最小值之间的差,将数据缩放到0到1之间。这样可以确保不同特征的值在相同的尺度上进行比较。
将上面封装成load data函数
def load_data():# 从文件导入数据datafile = './work/housing.data'data = np.fromfile(datafile, sep=' ')# 每条数据包括14项,其中前面13项是影响因素,第14项是相应的房屋价格中位数feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]feature_num = len(feature_names)# 将原始数据进行Reshape,变成[N, 14]这样的形状data = data.reshape([data.shape[0] // feature_num, feature_num])# 将原数据集拆分成训练集和测试集# 这里使用80%的数据做训练,20%的数据做测试# 测试集和训练集必须是没有交集的ratio = 0.8offset = int(data.shape[0] * ratio)training_data = data[:offset]# 计算训练集的最大值,最小值maximums, minimums = training_data.max(axis=0), training_data.min(axis=0)# 对数据进行归一化处理for i in range(feature_num):data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])# 训练集和测试集的划分比例training_data = data[:offset]test_data = data[offset:]return training_data, test_data# 获取数据 training_data, test_data = load_data() x = training_data[:, :-1] y = training_data[:, -1:]# 查看数据 print(x[0]) print(y[0])
二. 模型设计
完整封装运行代码:
class Network(object):def __init__(self, num_of_weights):# 随机产生w的初始值# 为了保持程序每次运行结果的一致性,此处设置固定的随机数种子np.random.seed(0)self.w = np.random.randn(num_of_weights, 1)//num_of_weights表示权重的数量,函数生成形状为(num_of_weights, 1)的随机权重数组self.w[5] = -100.self.w[9] = -100.self.b = 0.//将self.b初始化为0,表示偏置项。def forward(self, x)://前向传播z = np.dot(x, self.w) + self.breturn zdef loss(self, z, y):error = z - ycost = error * errorcost = np.mean(cost)return costdef gradient(self, x, y):z = self.forward(x)gradient_w = (z-y)*xgradient_w = np.mean(gradient_w, axis=0)//# axis = 0 表示把每一行做相加然后再除以总的行数,mean算平均数gradient_w = gradient_w[:, np.newaxis]//使用NumPy的矩阵操作方便地完成了gradient的计算,但引入了一个问题,gradient_w的形状是(13,),而www的维度是(13, 1)。导致该问题的原因是使用np.mean函数时消除了第0维。为了加减乘除等计算方便,gradient_w和www必须保持一致的形状。因此我们将gradient_w的维度也设置为(13,1)gradient_b = (z - y)gradient_b = np.mean(gradient_b)return gradient_w, gradient_bdef update(self, gradient_w5, gradient_w9, eta=0.01):net.w[5] = net.w[5] - eta * gradient_w5net.w[9] = net.w[9] - eta * gradient_w9def train(self, x, y, iterations=100, eta=0.01):points = []losses = []for i in range(iterations):points.append([net.w[5][0], net.w[9][0]])z = self.forward(x)L = self.loss(z, y)gradient_w, gradient_b = self.gradient(x, y)gradient_w5 = gradient_w[5][0]gradient_w9 = gradient_w[9][0]self.update(gradient_w5, gradient_w9, eta)losses.append(L)if i % 50 == 0:print('iter {}, point {}, loss {}'.format(i, [net.w[5][0], net.w[9][0]], L))return points, losses# 获取数据 train_data, test_data = load_data() x = train_data[:, :-1] y = train_data[:, -1:] # 创建网络 net = Network(13) num_iterations=2000 # 启动训练 points, losses = net.train(x, y, iterations=num_iterations, eta=0.01)# 画出损失函数的变化趋势 plot_x = np.arange(num_iterations) plot_y = np.array(losses) plt.plot(plot_x, plot_y) plt.show()
根据loss值进行梯度计算
控制部分变量的变化图像:
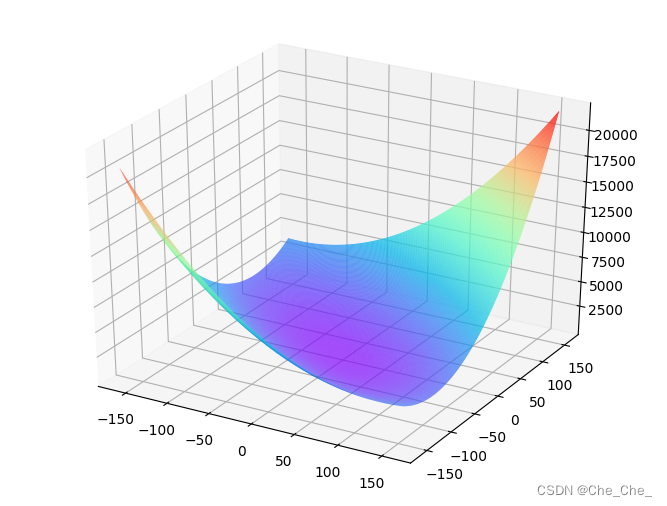
net = Network(13) # 此处可以一次性计算多个样本的预测值和损失函数 x1 = x[0:3] y1 = y[0:3] z = net.forward(x1) print('predict: ', z) loss = net.loss(z, y1) print('loss:', loss)这里将w0,w1,...,w12w_0, w_1, ..., w_{12}w0,w1,...,w12中除w5,w9w_5, w_9w5,w9之外的参数和bbb都固定下来,可以用图画出L(w5,w9)L(w_5, w_9)L(w5,w9)的形式,并在三维空间中画出损失函数随参数变化的曲面图。
net = Network(13) losses = [] #只画出参数w5和w9在区间[-160, 160]的曲线部分,以及包含损失函数的极值 w5 = np.arange(-160.0, 160.0, 1.0) w9 = np.arange(-160.0, 160.0, 1.0) losses = np.zeros([len(w5), len(w9)])#计算设定区域内每个参数取值所对应的Loss for i in range(len(w5)):for j in range(len(w9)):net.w[5] = w5[i]net.w[9] = w9[j]z = net.forward(x)loss = net.loss(z, y)losses[i, j] = loss# 使用matplotlib将两个变量和对应的Loss作3D图 import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D fig = plt.figure()# 如果您使用较新版本的matplotlib无法出图,可以替换为ax = fig.add_axes(Axes3D(fig)) ax = Axes3D(fig)w5, w9 = np.meshgrid(w5, w9)ax.plot_surface(w5, w9, losses, rstride=1, cstride=1, cmap='rainbow') plt.show()
这篇关于机器学习-波士顿房价预测的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!










