图灵机：计算机科学的奠基之作

本文主要是介绍图灵机：计算机科学的奠基之作，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

图灵机的概念由英国数学家阿兰·图灵在1936年提出，这个时期正是计算机科学的黎明时分。那个时候，人们还在使用机械计算器进行计算，而且这些计算器的功能都非常有限。

图灵提出这个概念的初衷，是为了解决所谓的“判定问题”，为了不让大家费脑子，这里我们就不具体说了。虽然图灵没能解决这个问题，但是他研究问题时提出的图灵机却为计算机科学奠定了基础。

图灵机包括无限长的纸带、读写头、状态寄存器等元素，这些元素共同模拟了人脑进行计算的过程。

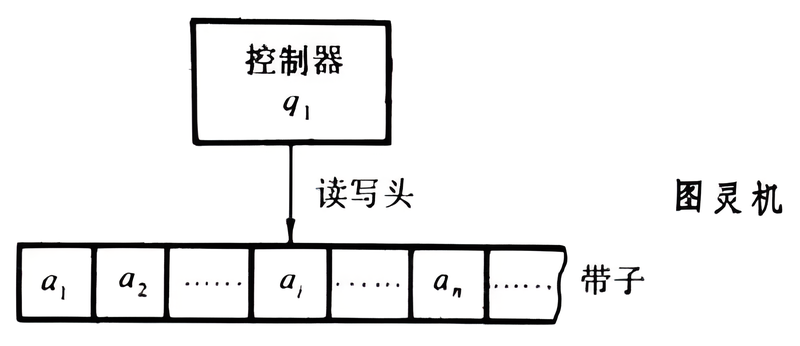
图灵机的提出，开启了一种全新的计算方式。虽然图灵机看起来很抽象，甚至有些神秘，但它却是现代计算机的基石。无论是大家日常使用的电脑、平板、手机，还是最新的超级计算机，甚至是区块链技术，它们的运行原理，都可以在图灵机这个模型中找到影子。因此，理解了图灵机，才能说我们打开了计算机技术的大门。

什么是图灵机

图灵机，这个名字听起来很神秘，但它其实就是一种抽象的计算机模型。它可以解决任何可计算的问题，虽然没有严格的证明，但是这已经被广大科学家所接受。

那么，什么是可计算的问题呢？

简单来说，就是存在某个算法，使用任何输入参数都能得出答案。比如“1+1=?”，或者“1<2”，这些都是可计算的问题。

什么是不可计算的问题呢？比如“停机问题”，它说的是：不存在一个算法或程序，能够对任意的程序和输入，预先判断出这个程序是否会停止。这个问题比较有意思，直觉上感觉不可能，比如死循环有时候是可以被判断出来的，但是这个结论是可以被证明的，有兴趣的同学可以继续了解下。

还有一些问题不属于计算问题，比如，我们常常烦恼的“晚上吃什么”这样的问题，就不属于计算问题，因为这个问题没有一个固定的算法可以解决。

结构和计算过程

接下来，让我们来看看图灵机的结构。它主要由以下几部分组成：

一条无限长的纸带，分成相邻的小格子，每个小格子最多写入一个字符。
一个字符表，包括纸带上可以出现的所有字符和一个空白字符。
一个读写头，可以读写纸带格子中的内容，并可以左右移动一个格子。
一个状态寄存器，记录机器每一步运算过程中机器所处的状态。
一个有限的指令集，记录读写头在某些特定情况下应该执行的指令。

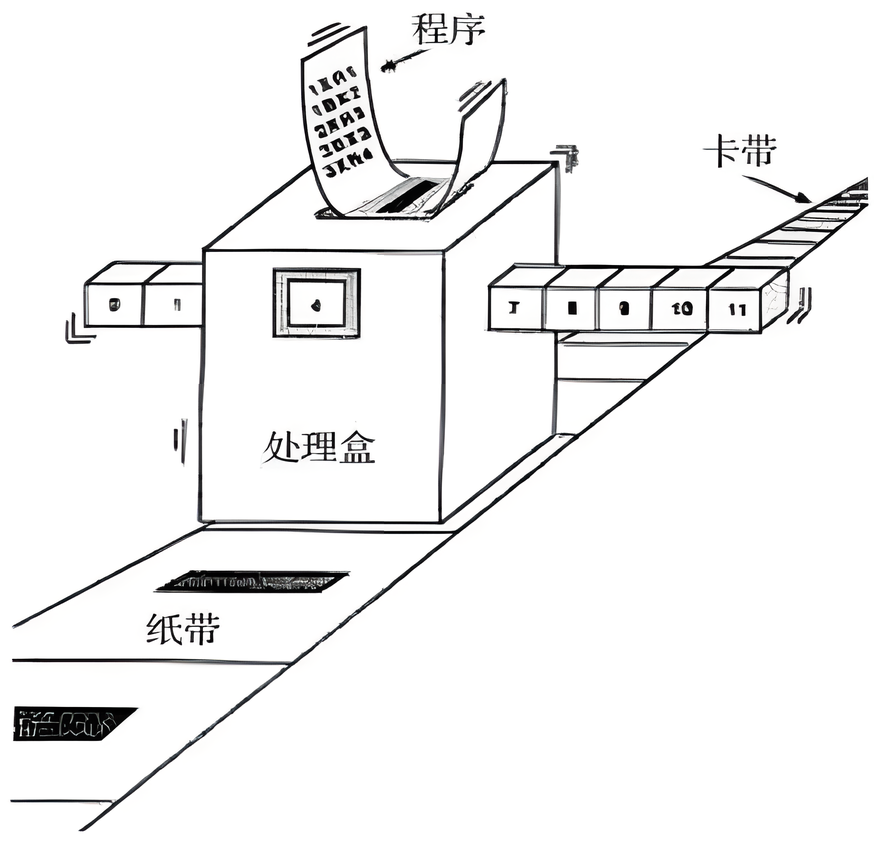
图灵机的计算过程就像是一个精心编排的舞蹈。读写头从纸带某一位置开始，严格按照当前所处的位置和格子的内容，根据指令集中的定义执行操作，直到状态变为停止，运算结束。此时纸带上留下的信息，即字符的序列便为输出。

你可以把它想象成一个勤奋的小工人，他按照规定的步骤，一步一步地完成任务，直到整个工作完成。这就是图灵机的计算过程。

现代计算机的设计理念，其实就是图灵机的一种实现。我们通常所说的冯诺依曼体系结构，就是基于图灵机模型的，大家想想计算机的几个主要组成部分：处理器（控制器和运算器）、存储器（内存）、各种输入输出设备，完全符合图灵机的结构定义，计算过程也是：控制器从内存按照顺序读取指令，交给运算器执行，然后再把结果写入到内存中。虽然内存实际是有限的，但是通过外置存储实际上可以无限扩充存储空间。