【卡方检验（Chi-Squared Test）的原理简介】

本文主要是介绍【卡方检验（Chi-Squared Test）的原理简介】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

卡方检验（Chi-Squared Test）的原理简介
- 1. 卡方检验的流程
- 借助scipy进行卡方检验
- 3 连续变量的卡方检验
- 4 借助sklearn进行卡方检验特征筛选

卡方检验（Chi-Squared Test）的原理简介

在一般情况下，卡方检验是针对于离散变量的独立性检验，卡方检验的零假设为两个离散变量相互独立。很明显，如果我们将其用于标签和特征的判别，就能借此判断某特征和标签是不是独立的，如果是，则说明特征对标签的预测毫无帮助。因此在很多时候，卡方检验都是非常重要的剔除无关特征的方法。

1. 卡方检验的流程

下面我们来看看卡方检验的具体流程：

假设我们有一组数据，想要确定性别和对某一问题的支持是否存在相关性。

Step1. 提出假设

假设检验的过程往往是采用了类似“反证法”的方法进行论证，例如如果我想证明这枚硬币是质地均匀的，那么在论证之前，我需要提出一个相反的假设，即这枚硬币有问题、质地不均匀，该假设会被记为𝐻₀，也就是所谓的零假设。当然既然是假设，就肯定有假设不成立的时候，此时假设结论的对立假设就是这枚硬币没有问题、是质地均匀的，该假设会被记为𝐻₁，也被称为备择假设或者对立假设。

目前假设情况如下：
H₀: 性别和对某一问题的支持不存在相关性
H₁：性别和对某一问题的支持存在相关性

Step2. 采集数据

import pandas as pddata = {'支持': [80, 60],'反对': [50, 70],'无意见': [20, 30]
}df = pd.DataFrame(data, index=['男性', '女性'])
print(df)

运行这段代码将生成如下的数据表：
在这里插入图片描述

Step 3.设计统计量

–	支持	反对	无意见	性别_all
男性	80	50	20	150
女性	60	70	30	160
态度_all	140	120	50	310

态度的取值分布如下：
$\frac {140} {310}\approx0.452$
$\frac {120} {310}\approx0.387$
$\frac {50} {310}\approx0.161$
同时，性别的取值分布如下：
$\frac{150} {310}\approx0.484$
$\frac{160} {310}\approx0.516$
现依据零假设，性别和态度相互独立，因此对于任意一名被调查者，同时性别=男性且态度=支持的概率为：
𝑃(性别=男性，态度=支持)=𝑃(性别=男性)∗𝑃(态度=支持)=0.484∗0.452=0.219
Notes:根据联合概率计算公式，当A、B两个随机变量相互独立时，𝑃(𝐴,𝐵)=𝑃(𝐴)∗𝑃(𝐵)
而目前，总共有310名被调查者，因此在零假设的情况下，性别=男性且态度=支持的被调查者总数期望为：
𝐸_{男性，支持}=𝑃(性别=男性，态度=支持)∗310=0.219*310=68
而真实的统计结果是性别=男性且态度=支持总被调查者有80人，和期望人数有些差异，很明显，当实际人数和期望人数的差异越大，我们就越有理由怀疑零假设。但这种差异是不能通过性别和态度的一组取值结果来判定，我们还需要进一步查看列联表中其他位置的期望频数

–	支持	反对	无意见
男性	68	58	24
女性	72	62	26

对比统计频数表：

–	支持	反对	无意见
男性	80	50	20
女性	60	70	30

为了衡量二者的差异，我们可以构造如下统计量：
$\mathcal{X}^2 = \sum_{i=1}^{m}\sum_{j=1}^{n}\frac{(O_{i,j}-E_{i,j})^2}{E_{i,j}}$
其中i、j代表列联表的行和列，𝑂_𝑖,𝑗表示i行j列的观测值（observe）、𝐸_𝑖,𝑗表示期望值。而此处的X 就是卡方值，也就是卡方检验中的统计量。我们可以通过如下方式进行卡方值的计算：
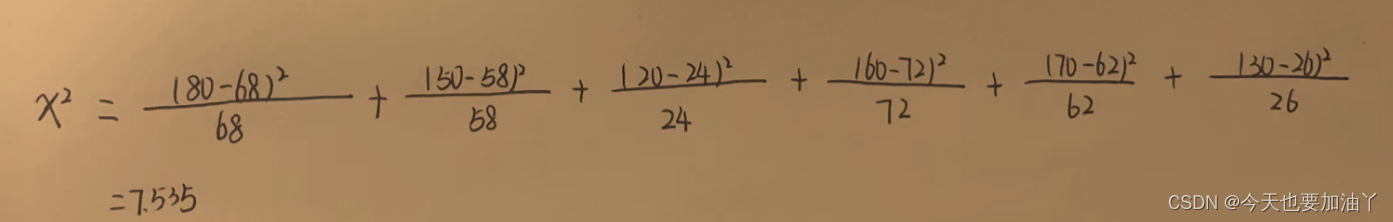
在这里插入图片描述
对于二维列联表来说，自由度就是(𝑚−1)∗(𝑛−1)
，行数-1和列数-1的乘积：
（2-1)*(3-1)=2

借助scipy进行卡方检验

当然，上述过程我们也可以通过scipy快速执行，这里我们需要调用scipy模块下的stats模块，并借助其中chi2_contingency函数完成相关计算：

from scipy import stats
stats.chi2_contingency(observed = df)

在这里插入图片描述
chi2_contingency函数返回了四个结果，分别是卡方值、概率值、自由度以及期望频数表，和我们此前手动计算结果不完全一致，这可能是手动计算时四舍五入了，下面由计算机手动计算

需要注意的是，这里的p值既是事件发生的概率，同时也是我们后续在进行特征筛选时的一个评分，类似相关系数，p值越小说明越不独立，也就是说明这两个变量关联性越强。当然，除了p值意外，卡方值也可以作为评估关联性强弱的评分，卡方值越大、p值越小、不相关的假设越不成立、变量越相关。

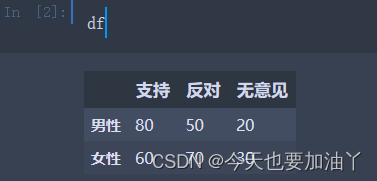
import pandas as pddata = {'支持': [80, 60],'反对': [50, 70],'无意见': [20, 30]
}df = pd.DataFrame(data, index=['男性', '女性'])
print(df)

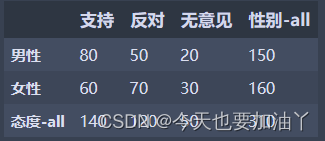
在这里插入图片描述
对df表按行按列汇总

df_count_all = df.copy()df_count_all.loc['态度-all'] = df.sum(0)
df_count_all['性别-all'] = df_count_all.sum(1)
df_count_all

在这里插入图片描述
计算期望频数表。对于每个单元格，期望频数的计算应该是(性别_𝑎𝑙𝑙[𝑖]/𝑡𝑜𝑙)∗(态度_𝑎𝑙𝑙[𝑗]/𝑡𝑜𝑙)∗𝑡𝑜𝑙
，等于性别_𝑎𝑙𝑙[𝑖]∗态度_𝑎𝑙𝑙[𝑗]/𝑡𝑜𝑙

from itertools import product
性别_all = df_count_all.loc[:,'性别-all'].copy()
态度_all = df_count_all.loc[ '态度-all',:].copy()
for i, j in product(range(2), range(3)):Eij = 性别_all[i] * 态度_all[j] / toldf_temp.iloc[i, j] = Eij

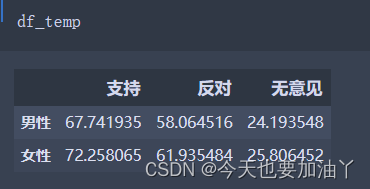
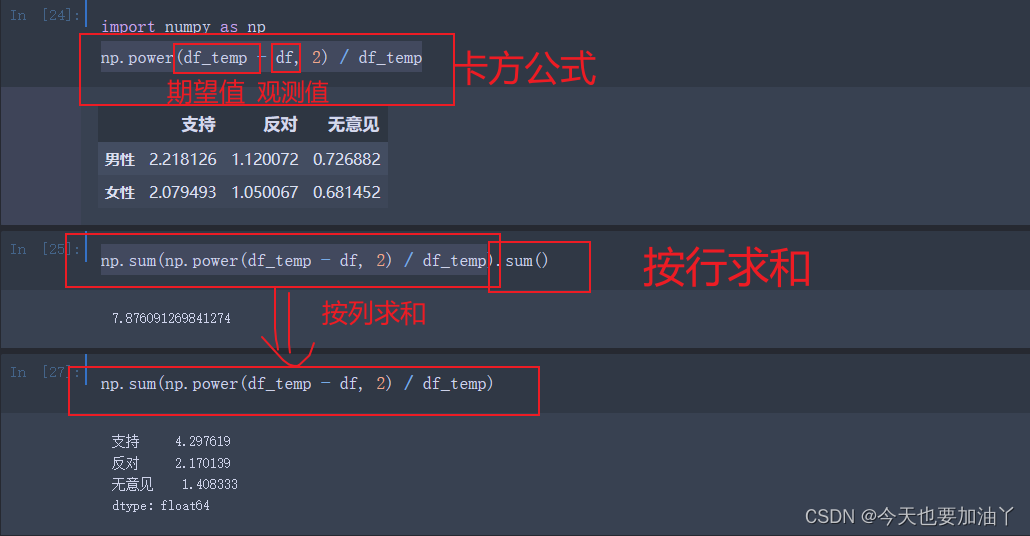
在这里插入图片描述

至此，卡方值和chi2_contingency计算一样，我们完成了卡方值的手动计算流程。

3 连续变量的卡方检验

接下来，我们就可以考虑借助sklearn中的相关函数，通过卡方检验来进行特征筛选。不过这里需要注意的是，通常来说卡方检验是作用于离散变量之间的独立性检验，但sklearn中的卡方检验只需要参与检验的其中标签是离散特征即可，即sklearn中的卡方检验不仅可以作用于两个离散变量、还可以作用于连续变量和离散变量之间，因此我们这里需要补充介绍关于连续变量与离散变量之间的卡方检验计算流程，而在连续变量和离散变量的卡方检验中，自由度是离散变量类别数-1，也就是2-1=1

# 生成随机的连续变量和二分类变量
np.random.seed(0)
continuous_variable = np.random.rand(10)
binary_variable = np.random.choice([0, 1], size=10)# 创建包含连续变量和二分类变量的DataFrame
df = pd.DataFrame({'ContinuousVariable': continuous_variable, 'Binaryariable': binary_variable})# 打印DataFrame
print(df)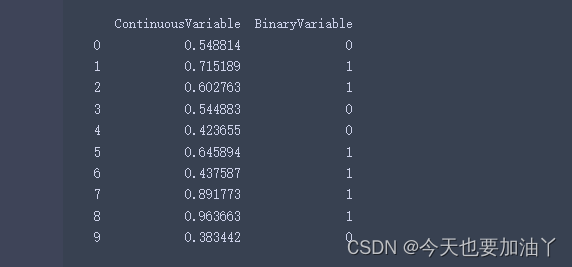

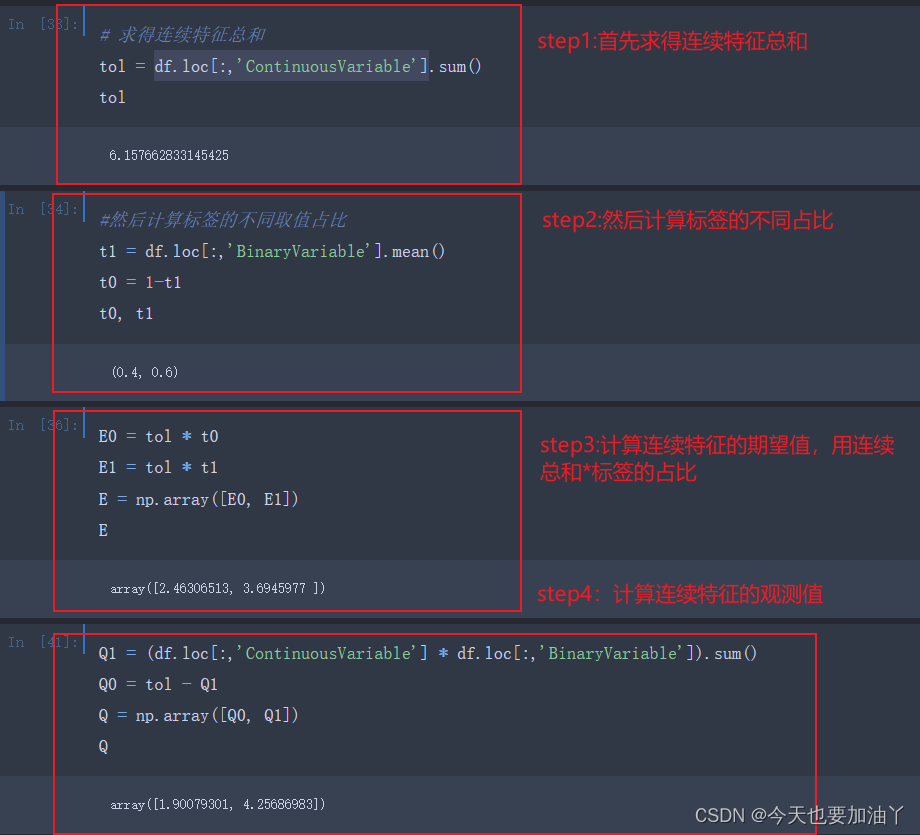
在这里插入图片描述

但需要注意的是，连续变量的取值毕竟不是频数结果，最终的卡方值会严重受到连续变量的量纲影响，而这种影响对统计推断而言是无意义的。因此，在实际进行连续变量的卡方检验过程中，建议先对原始变量进行标准化处理，该过程会将所有连续变量取值放缩至类似水平，同样也会将p值和卡方值放缩至同样水平，然后我们在单独针对连续变量进行BestK筛选，而不建议同时比较连续变量和离散变量的K值然后在一个流程中进行筛选（因为连续变量的p值和卡方值没有绝对大小的意义）

4 借助sklearn进行卡方检验特征筛选

sklearn其实是采用类似连续变量的卡方检验流程来进行的离散变量卡方检验。其实这也并不奇怪，对于sklearn来说，默认是不区分连续变量和离散变量的。并且计算过程中的自由度也不再是列联表行数-1和列数-1相乘的结果，而是标签取值水平-1。那就是可以统一自由度。原生的卡方检验的自由度是同时受到两个离散变量类别个数影响，此时带入不同离散变量时自由度可能不同，而不同的自由度将影响评分数值绝对值的有效性（自由度越高对评分大值容忍度就越高）

我们尝试借助sklearn进行基于卡方检验的特征筛选。该过程同样涉及评分函数和筛选评估器两部分，此处筛选评估器仍然选用SelectKBest，而卡方检验的评分函数是chi2：在最终的SelectKBest筛选过程，实际上是按照卡方值的大小，筛选卡方值最大的k个特征(不是按照p值进行筛选)。根据卡方检验的计算流程，卡方值不会存在负数情况，并且卡方值越大、说明变量之间关联关系越强。相关实现流程如下

from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
import numpy as np# 加载示例数据集
iris = load_iris()
X, y = iris.data, iris.target
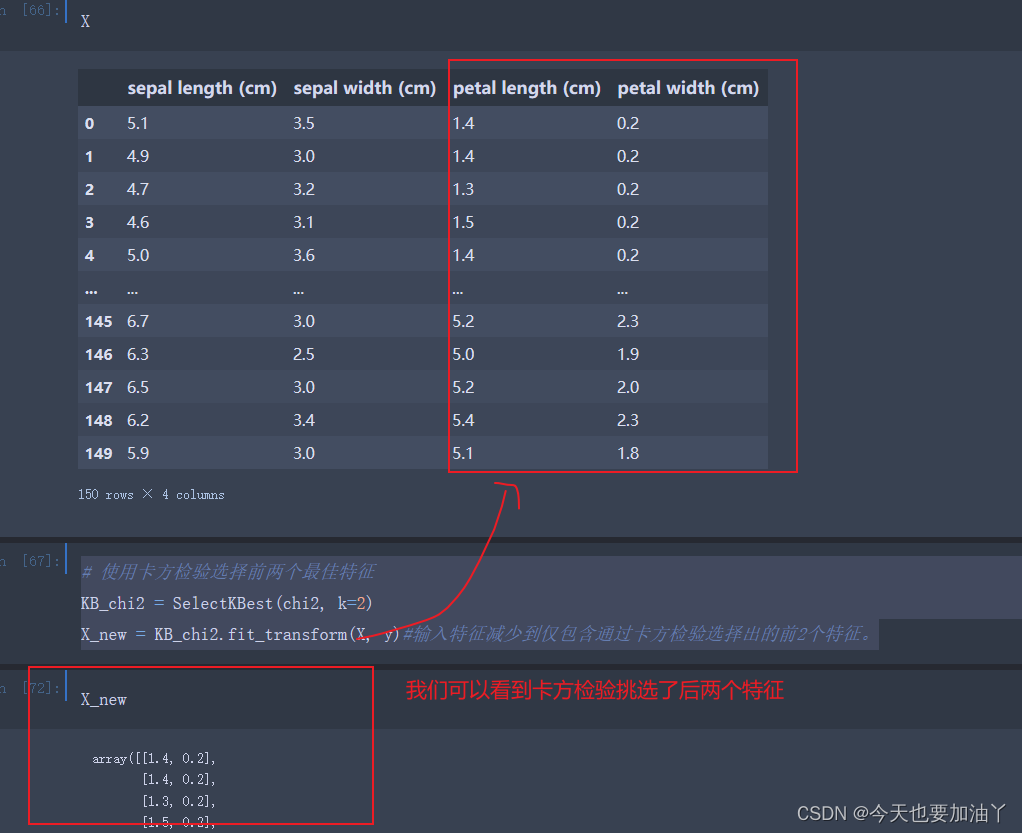
X = pd.DataFrame(X,columns=iris.feature_names)

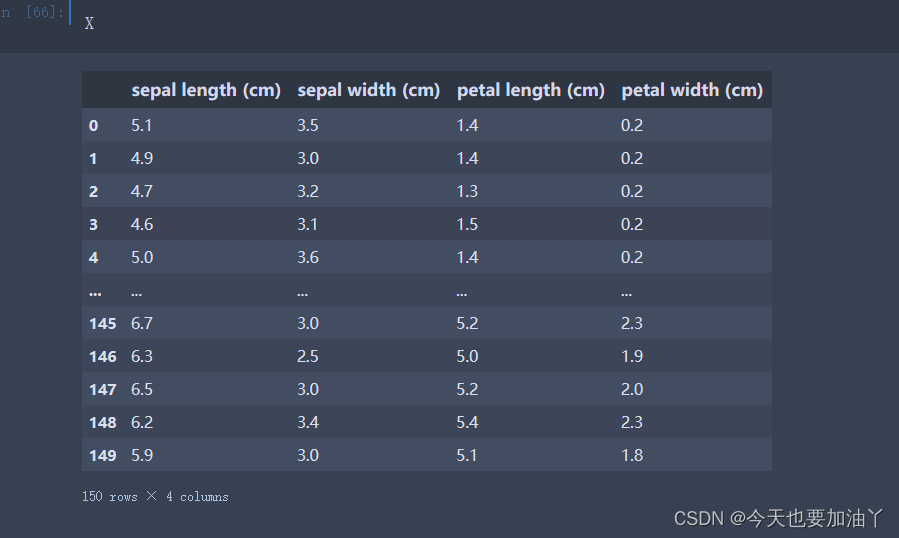
在这里插入图片描述

# 使用卡方检验选择前两个最佳特征
KB_chi2 = SelectKBest(chi2, k=2)
X_new = KB_chi2.fit_transform(X, y)#输入特征减少到仅包含通过卡方检验选择出的前2个特征。

在这里插入图片描述

KB_chi2.scores_
#KB_chi2.scores_是指使用chi2统计测试后，每个特征的得分。
#在SelectKBest中，使用chi2统计测试对每个特征进行评分，表示该特征与目标变量之间的相关性或关联程度。
#得分越高表示特征与目标变量之间的关联程度越高。

在这里插入图片描述

KB_chi2.pvalues_#KB_chi2.pvalues_指的是使用chi2统计测试后，每个特征的p值。
#在统计学中，p值表示观察到的数据与原假设一致的概率。
#在特征选择中，p值可以用来衡量特征与目标变量之间的相关性。较低的p值表示特征与目标变量之间的关联性较高。

在这里插入图片描述

def SelectName(Select, KBest=True):"""根据特征筛选评估器进行列名称输出函数:param Select: 训练后的特征筛选评估器:param KBest: 是否是挑选评分最高的若干个特征:return：保留特征的列名称"""if KBest == True:K = Select.kelse:l = np.array(range(Select.n_features_in_))K = (l > np.percentile(l, 100 - Select.percentile)).sum()threshold = sorted(Select.scores_, reverse=True)[K-1]col_names = []for score, col in zip(Select.scores_, Select.feature_names_in_):if score >= threshold:col_names.append(col)return col_names