半数集-递归

1 问题

给定一个自然数n，由n 开始可以依次产生半数集set(n)中的数如下。
(1) n∈set(n)；
(2) 在n 的左边加上一个自然数，但该自然数不能超过最近添加的数的一半；
(3) 按此规则进行处理，直到不能再添加自然数为止。
例如，set(6)={6,16,26,126,36,136}。半数集set(6)中有6 个元素。
注意半数集是多重集。
对于给定的自然数n，计算半数集set(n)中的元素个数。

2 分析

1. 半数集：给定一个数，在这个数的左边添加新的数字，新添加的数字应该小于或等于这个数的第一个数字的一半，这些数字构成的集合就是半数集.
2. 举例：6的半数集求解过程如下：
   
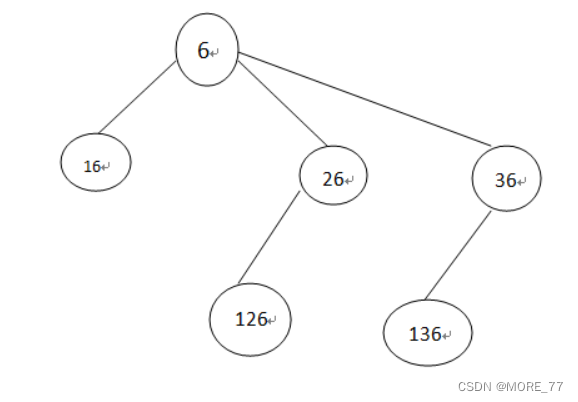
   6的一半是3，因此6的左边可以添加1,2,3,获得数字16，26，36；
   26的左边的第一数字2的一半是1，因此可以添加1，获得数字126；
   36的左边的第一位数字3的一半是1.5，因此可以添加1，获得数字136；
   因此6的半数集就是6，16，26，36，126，136。

在求解过程中，要求6的半数集就得先求16,26,36的半数集，因此就构成了递归。

AC 代码

#include<iostream>
using namespace std;
int a[1005];//存储已经计算过的数据 
int f(int n){//计算数字n的半数集int sum=1;if(a[n]>0)//如果f(n)已经计算过一次了，就不再重复计算 return a[n];for(int i=1;i<=n/2;i++)//前方能加sum+=f(i);a[n]=sum;return sum;
}
int main(){int n;cin>>n;cout<<f(n)<<"\n";
}

分析

递归，T(n)=T(n/2),时间复杂度为O（n）