NOIP-2010-J1-真题解析

一、选择题

1、D，基础题，考察科学计数法
2、A，基础题，一个字节8个bit
3、A，基础题，考察逻辑运算
4、D，基础题，与windows不同，Linux的文件是否可执行与其扩展名无直接关系，任何文件均可设置为可执行文件
5、A，数据结构题，考察满二叉树，n层的二叉树是满二叉树时，结点最多
6、D，基础题，考察计算机发展史
7、B，考察对进制的理解应用，由加法可得x+y=x，故y=0，x+z=x0，表示产生了进位，则x=1,z=2，所以xyzx=1021=210，即zxy
8、D，基础题，考察程序设计语言常识，Pascal, C/C++属于编译性语言
9、C，考察前缀表达式，将其转为中缀表达式，从右至左，操作数入栈，遇到操作符，则弹出两个操作数运算，将运算结果入栈，然后继续遍历，直至遍历结束，最后栈里的元素就是运算结果，这里转为中缀表达式是(5+12)2+3=37
10、B，基础题，考察计算机硬件系统，CPU中引入高速缓存，即Cache，来提高CPU存取数据的速度
11、D，基础题，考察补码，由补码推原码，对于负数，符号位不变，数据位最低位减1，得到反码，然后数据位全部取反，得到原码
12、B，考察排序算法时间复杂度，基于比较的排序算法的时间复杂度下限是nlogn
13、B，举特例观察，例如53，53的二进制数为110101，可以看出与nlog₂ 10接近，故选B
14、B，考察计算机网络常识，HTML常识
15、B，考察栈的入栈出栈序列，如果R3第一个出栈，则此刻R1,R2必然还在栈里，所以第5个，即最后一个出栈的不可能是R2，因为R1肯定是在R2后面出栈的
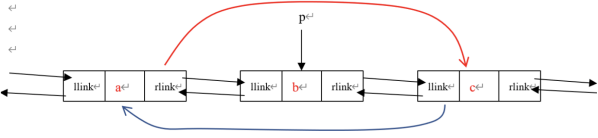
16、A，考察双向链表的删除操作，A选项将P的后继的前驱改为指向P的后继，P的前驱的后继指向改为P的前驱，这样链表在P结点处就中断了

17、A，考察树的遍历，不论哪种遍历方式，根节点的左子树和右子树的结点在遍历序列里肯定是紧靠在一起的，根据前序和后序确定根节点是A，然后观察可得B和C是左子树的结点
18、D，考察图的拓扑排序，拓扑排序是针对DAG，有向无环图的，且排序序列通常不唯一，当图不连通时，即有多个连通子图的时候，入度为0的结点可能排在入度大于0的结点后面，比如图：1–>3, 2，两个子图，拓扑排序可以是1->3->2，则2排在了3后面
19、C，考察二叉树的顺序存储，结点k的左右孩子节点分别是2k, 2k+1，反推，若已知节点k，则其父结点下标，则是k/2下取整
20、D，考察竞赛常识，NOI系列活动由中国计算机协会CCF主办

二、问题求解

1、直接模拟可得结果：2-2-1-2-3-1-1-3-4-3-1-2-1-3-5-3-6
2、数学题，数字8划分为3个非零整数，然后做排列，8划分3只有5种，(1,1,6),(1,2,5),(1,3,4),(2,2,4),(2,3,3)，然后枚举队列快照元素数量分别是0个，1个，2个，3个的情况即可，总数是49个

三、阅读程序

1、

#include <iostream>
using namespace std;void swap(int & a, int & b)
{int t;t = a;a = b;b = t;
}int main()
{int a1, a2, a3, x;cin>>a1>>a2>>a3;if (a1 > a2)swap(a1, a2);if (a2 > a3)swap(a2, a3);if (a1 > a2)swap(a1, a2);cin>>x;if (x < a2)if (x < a1)cout<<x<<' '<<a1<<' '<<a2<<' '<<a3<<endl;elsecout<<a1<<' '<<x<<' '<<a2<<' '<<a3<<endl;elseif (x < a3)cout<<a1<<' '<<a2<<' '<<x<<' '<<a3<<endl;elsecout<<a1<<' '<<a2<<' '<<a3<<' '<<x<<endl;    return 0;
}

输入：

91 2 20
77

考察if分支语句，输出为：2 20 77 91

2、

#include <iostream>
using namespace std;int rSum(int j)
{int sum = 0;while (j != 0) {sum = sum * 10 + (j % 10);j = j / 10;}return sum;
}int main()
{int n, m, i;cin>>n>>m;for (i = n; i < m; i++)if (i == rSum(i))cout<<i<<' ';return 0;
}

输入：
90 120

简单算法题，求指定范围内的回文数字，90-120之间的回文数字有哪些，输出这些数字以空格隔开，结果是：
99 101 111

3、

#include <iostream>
#include <string>
using namespace std;int main()
{string s;char m1, m2;int i;getline(cin, s);m1 = ' ';m2 = ' ';for (i = 0; i < s.length(); i++)if (s[i] > m1) {m2 = m1;m1 = s[i];}else if (s[i] > m2)m2 = s[i];cout<<int(m1)<<' '<<int(m2)<<endl;return 0;
} 

输入：
Expo 2010 Shanghai China

分析代码可知，这里求的是输入字符串中最大的字符和第二大的字符，结果分别是’x’, ‘p’，代码要输出的是字符的ASCII码，根据字母表顺序以及’a’的码值是97，则’x’, 'p’分别是120，112

4、

#include <iostream>
using namespace std;const int NUM = 5;int r(int n)
{int i;if (n <= NUM)return n;for (i = 1; i <= NUM; i++)if (r(n - i) < 0)return i;return -1;
}int main()
{int n;cin>>n;cout<<r(n)<<endl;return 0;
}

1）
输入：7
输出：
2）
输入：16
输出：

打表可以发现函数r的值呈周期性的变化：

周期为6，以1，2，3，4，5，-1这6个值周期性变化
所以结果分别是1，4

四、完善程序
1、哥德巴赫猜想）哥德巴赫猜想是指，任一大于2的偶数都可写成两个质数之和。迄今为止，这仍然是一个著名的世界难题，被誉为数学王冠上的明珠。试编写程序，验证任一大于2且不超过n的偶数都能写成两个质数之和。

#include <iostream>
using namespace std;int main()
{const int SIZE = 1000;int n, r, p[SIZE], i, j, k, ans;bool tmp;cin>>n;r = 1;p[1] = 2;for (i = 3; i <= n; i++) {[    ①    ];for (j = 1; j <= r; j++)if (i % [     ②   ]  == 0) {tmp = false;break;}if (tmp) {r++;[    ③   ] ;}}ans = 0;for (i = 2; i <= n / 2; i++) {tmp = false;for (j = 1; j <= r; j++)for (k = j; k <= r; k++)if (i + i == [     ④   ] ) {tmp = true;break;}if (tmp)ans++;}cout<<ans<<endl;return 0;
}

若输入n为2010，则输出[ ⑤ ]时表示验证成功，即大于2且不超过2010的偶数都满足哥德巴赫猜想。

阅读代码可以发现p数组是枚举出了2~n之间的所有的质数，这里是采用的线性筛（欧拉筛）算法，数组p按从小到大顺序记录了筛选出来的质数，对于当前数i，如果其能当前p数组任意一个数整除，则其不是质数，否则是质数。
然后枚举大于2且不超过n之间的所有偶数，判断其是否能写成两个质数之和。
① tmp=true，对应于后面for循环里的tmp=false
② p[j]，用p中已有质数去整除i，若均不能整除，则表示当前i是质数
③ p[r] = i
for(i=2;i<=n/2;i++)是遍历[2, n]之间的所有偶数，判断其是否都能写成两个质数之和。
④ p[j] + p[k]，枚举p数组中任意两个质数的和，判断其是否等于2i
⑤ 1004，若验证成功，则大于2且不超过2010的偶数有1005-1=1004个，这1004个偶数都判断成功了，ans值为1004

2、(过河问题）在一个月黑风高的夜晚，有一群人在河的右岸，想通过唯一的一根独木桥走到河的左岸。在这伸手不见五指的黑夜里，过桥时必须借助灯光来照明，很不幸的是，他们只有一盏灯。另外，独木桥上最多承受两个人同时经过，否则将会坍塌。每个人单独过桥都需要一定的时间，不同的人需要的时间可能不同。两个人一起过桥时，由于只有一盏灯，所以需要的时间是较慢的那个人单独过桥时所花的时间。现输入n（2≤n<100）和这n个人单独过桥时需要的时间，请计算总共最少需要多少时间，他们才能全部到达河的左岸。 例如，有3个人甲、乙、丙，他们单独过桥的时间分别为1、2、4，则总共最少需要的时间为7。具体方法是：甲、乙一起过桥到河的左岸，甲单独回到河的右岸将灯带回，然后甲、丙再一起过桥到河的左岸，总时间为2+1+4=7。

#include <iostream>
using namespace std;const int SIZE = 100;
const int INFINITY = 10000;
const bool LEFT = true;
const bool RIGHT = false;
const bool LEFT_TO_RIGHT = true;
const bool RIGHT_TO_LEFT = false;int n, hour[SIZE];
bool pos[SIZE];int max(int a, int b)
{if (a > b)return a;elsereturn b;
}int go(bool stage)
{int i, j, num, tmp, ans;if (stage == RIGHT_TO_LEFT) {num = 0;ans = 0;for (i = 1; i <= n; i++)if (pos[i] == RIGHT) {num++;if (hour[i] > ans)ans = hour[i];}if ([    ①    ])return ans;ans = INFINITY;for (i = 1; i <= n - 1; i++)if (pos[i] == RIGHT)for (j = i + 1; j <= n; j++)if (pos[j] == RIGHT) {pos[i] = LEFT;pos[j] = LEFT;tmp = max(hour[i], hour[j]) +[     ②    ];if (tmp < ans)ans = tmp;pos[i] = RIGHT;pos[j] = RIGHT;}return ans;}if (stage == LEFT_TO_RIGHT) {ans = INFINITY;for (i = 1; i <= n; i++)if ([    ③    ]) {pos[i] = RIGHT;tmp =[    ④    ];if (tmp < ans)ans = tmp;[        ⑤    ];}return ans;}return 0;
}int main()
{int i;cin>>n;for (i = 1; i <=n; i++) {cin>>hour[i];pos[i] = RIGHT;}cout<<go(RIGHT_TO_LEFT)<<endl;return 0;
}

算法题，本题过河问题是经典的回溯算法应用，此题并不适用贪心算法，所以用回溯遍历了每一种过河选择情况，最终比较得到最小过河时间。
分析：若n<=2，则直接一趟过去，右→左，时间是较慢的人过河时间。
若n>2，则必然有多次往返，先是2人，右→左，然后1人，左→右，拿灯回来，然后重复这两步骤，直至最后右边剩余人数不超过2人，直接一趟到左边。

如图所示，n=3，abc3个人过河的回溯搜索树，每一条路径就是多次来回过河后最终都到达左边的方案，回溯遍历每一种方案，比较求得最少过河时间。

go是dfs递归函数，pos记录每一个人的状态，LEFT表示在左边，RIGHT表示在右边，go函数的参数是一个布尔变量stage，表示当前过河步骤是往右还是往左，如果是右往左，统计在右边即将可能要右→左过河的人数num，并求出过河最慢的那个人的过河时间ans。
如果① num<=2，则表示一趟即可结束，直接返回本次过河的最短时间ans。
否则遍历当前右边的这num个人的全部2人组合情况，依次尝试过河，两人编号分别是i，j，每种组合下的总过河时间是当前两人的较长的过河时间加上紧接着的左→右以及后续多次往返的过河的时间tmp， ② go(LEFT_RIGHT)
如果tmp比当前ans更小，则更新ans为tmp
递归遍历完返回后，恢复现场，将i，j归位到右边，继续递归遍历下一个i，j组合。

如果是左→右，则是1个人过河把灯取回，到右边，然后再与一人一起从右边到左边。
同样的，遍历当前在左边的每个人，尝试每一个人i过河的情况，过河时间等于i到右边的时间加上紧接着再过到左边以及后续多次来回往返的时间。
③ pos[i]=LEFT
④ hour[i]+go(RIGHT_TO_LEFT)
每尝试一个i，递归遍历结束后，求得总过河时间tmp，判断其是否小于当前ans，若是则更新ans，然后回溯，恢复现场，将i归位到右边，然后继续遍历下一个i。
主函数里，调用go函数，参数初值为RIGHT_TO_LEFT，因为第一次过河是从右到左。