本文主要是介绍HoudiniVex笔记_P7_Loop循环,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
原视频:https://www.youtube.com/playlist?list=PLzRzqTjuGIDhiXsP0hN3qBxAZ6lkVfGDI
Bili:Houdini最强VEX算法教程 - VEX for Algorithmic Design_哔哩哔哩_bilibili
Houdini版本:19.5
1、for循环
创建类型为detail的attributewrangle节点,写入下面代码
int num = chi('num');
for( int i=0; i<num; i++){满足i<num,就运行for内部代码一次,i每次递增1int pt = addpoint(0,set(i, 0, 0));}
//结果为 在场景窗口sence中创建了num个点
添加copytopoints节点,用小球Sphere代替点,结果为: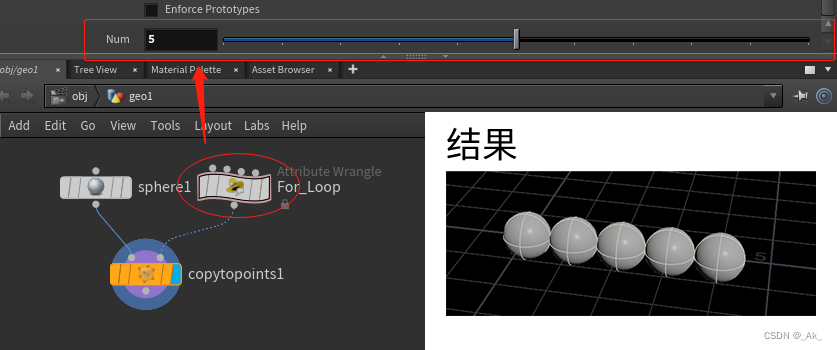
2、 for循环与属性
利用 npoints(geohandle) 函数统计第几个连接点输入的点数,在上面的attributewrangle(For_Loop)节点下方添加一个attributewrangle(For_Loop2)节点,输入以下代码:
for(int i=0; i<npoints(0); i++){vector col = rand(i * chf('seed')); //rand(seed) 根据种子seed随机返回一个0~1内的值setpointattrib(0, 'Cd', i, col); }
//遍历点,赋予随机颜色添加copytopoints节点,用小球Sphere代替点,结果为: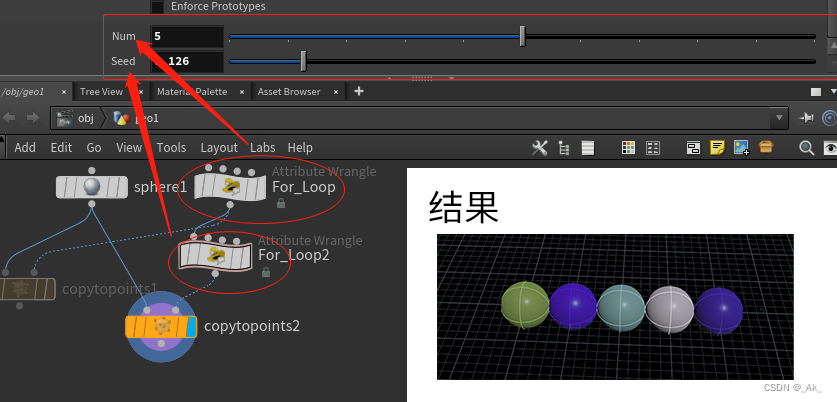
seed参数为0,则所有小球默认颜色为抹绿色(如图第一个小球颜色)。
3、for循环与螺旋曲线
利用for循环和三角函数创建螺旋曲线,开始之前,先讲讲三角函数。
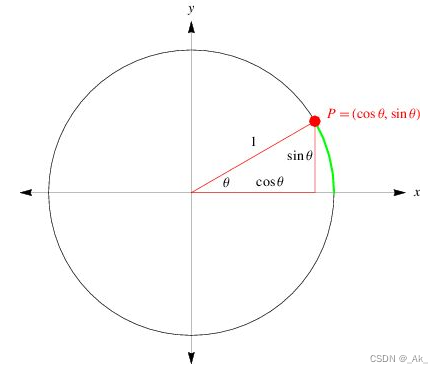
以二维直角坐标的原点为中心,画出一个半径为1的圆,将圆的半径从x轴旋转 θ度,从半径与圆弧相交的点作一条线垂直于x轴,这条垂线的长度就是正弦,以sinθ 表示。
即,半径为1的圆,角度为θ的x坐标为余弦cosθ(=邻边/斜边),y坐标为正弦sinθ(=对边/斜边)。
创建类型为detail的attributewrangle节点(Exercise_1),写入下面代码:
int num = chi('num'); //可适当把范围扩大
float angratio = chf('angratio'); //角度系数,控制点的密集度
float heightratio = chf('heightratio'); //高度系数,控制螺旋高度for(int i=0; i<num; i++){float x = cos(i * $PI * angratio); //$PI=180°,是Houdini的一个全局变量float z = sin(i * $PI * angratio);vector pos = set(x, i*heightratio, z); //y=0时,创建一个圆int pt = addpoint(0, pos);
} //结果为一条螺旋点
添加一个Add节点 ,点击Polygon设置为ByGroup,结果为: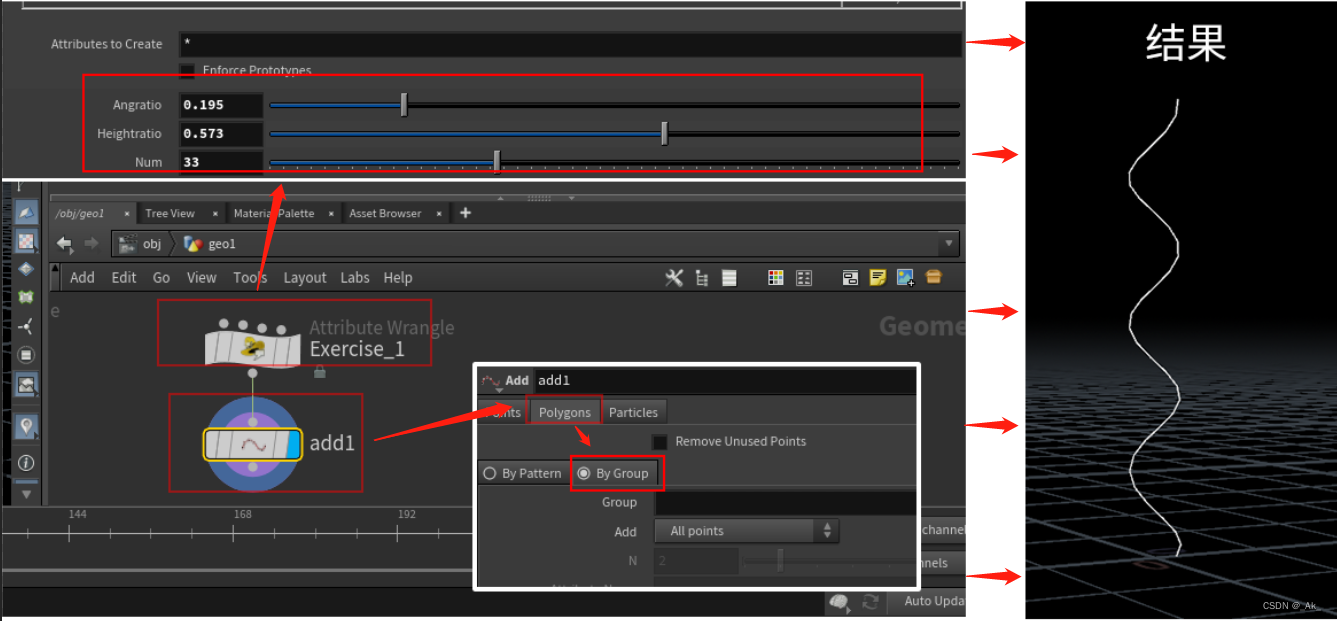
4、while循环
while循环与for循环相似,for循环重点在于可以控制循环的次数使用,while循环重点在于注重循环的条件。
使用while循环时注意别陷入无限循环。
创建类型为detail的attributewrangle节点(Whiel_Loop),写入下面代码:
int num = chi('num'); //点数
int i = 0;while(i<num){int pt = addpoint(0, set(i, 0, 0));i++;
} 添加copytopoints节点,用小球Sphere代替点,结果为:
5、do while循环
与while循环相似,但是至少运行一次(先运行一次,才进行条件判断)
创建类型为detail的attributewrangle节点(Do_Whiel_Loop),写入与上面while循环相似下面代码:
int num = chi('num');
int i = 0;do{int pt = addpoint(0, set(i, 0, 0));i++;
}while(i<num);num不为0,结果与【4】 的While循环结果相同。
6、while循环与螺旋曲线
创建类型为detail的attributewrangle节点(Exercise2),写入下面代码:
float totalang = $PI * chf('totalang'); //旋转多少圈,360°为1圈($PI=180°)//可适当加大范围
float angratio = chf('angratio'); //角度系数,控制角度
float heightratio = chf('heightratio'); //高度系数,控制高度
float currentang = 0.0;
float currentheight = 0.0;while(currentang < totalang){float x = cos(currentang);float z = sin(currentang);float y = currentheight;vector pos = set(x, y, z);int pt =addpoint(0, pos);currentheight += heightratio; //下一个点的高度currentang += $PI * angratio; //下一个点的角度
}//注意:angratio=0, totalratio≠0, 进入无限循环添加一个Add节点 ,点击Polygon设置为ByGroup,结果为:结果与【3、For循环练习—螺旋曲线】的结果相同。
7、foreach循环(与数组)
在foreach循环中,每次循环依次取数组或对象中的集合,取出放置在定义的变量中,遍历后退出循环。
创建类型为detail的attributewrangle节点(Creat_Array),写入下面代码:
int num = chi('num');int values[] = array();
for(int i=0; i<num; i++){push(values,i);}i[]@values = values; //创建一个values属性数组创建类型为detail的attributewrangle节点(Foreach_Loop),连接在上面的节点下方,写入下面代码:
int values2[] = i[]@values; //把上一个节点内的values[]数组传递给values2foreach(int val; values2){int pt = addpoint(0, set(val, 0, 0));//遍历数组,每次取值给变量val,根据val创建点}//结果为:num为多少,则在场景中依次创建多少个点添加copytopoints节点,用小球Sphere代替点,结果为:结果与【 4、while循环】的结果相同。
8、for循环与数组
主要是通过数组的索引访问数组。
eg.使用【7、foreach循环(与数组Array)】的attributewrangle节点(Creat_Array),再创建类型为detail的attributewrangle节点(For_Loop_to_access_array),连接在Creat_Array节点下方,写入下面代码:
int values3[] = i[]@values; 把上一个节点内的values[]数组传递给values3for(int i=0; i<len(values3); i++){ //len()函数返回数组长度int val = values3[i];int pt = addpoint(0, set(val, 0, 0));
}添加copytopoints节点,用小球Sphere代替点,结果为:结果与【 4、while循环】的结果相同。
9、for循环与螺旋曲线
这次使用立方体代替生成螺旋曲线,并控制立方体朝向。
创建类型为detail的attributewrangle节点(Exercise3),写入下面代码:
int num = chi('num'); //点数,可适当扩大范围
float angratio = chf('angratio'); //角度
float heightratio = chf('heightratio'); //高度//创建点的位置存储到数组positions
vector positions[] = array();
for(int i=0; i<num; i++){float x = cos($PI * angratio * i);float z = sin($PI * angratio * i);float y = i * heightratio;vector pos = set(x, y, z);push(positions, pos);
}//下面的循环,主要是利用前一个点控制后一个点的朝向
for(int i=0; i<len(positions)-1; i++){ //len()-1,最后一个点不作处理vector pos1 = positions[i];vector pos2 = positions[i+1];vector dir = pos2 - pos1;int pt = addpoint(0, pos1);setpointattrib(0, 'N', pt, dir); //利用前后点的向量差设置返现,即朝向setpointattrib(0, 'up', pt, set(0, 1, 0)); //排列小调整优化,后面向量再细说
} 添加copytopoints节点,用立方体box代替点,结果为:
结果依次为:不作优化改变、设置法线方向setpointattrib(0, 'N'),设置Y方向setpointattrib(0, 'up')
10、嵌套循环
创建类型为detail的attributewrangle节点(Nexted_Loop),写入下面代码:
int num1 = chi('num1');
int num2 = chi('num2');for(int i =0; i<num1; i++){for(int n=0; n<num2; n++){//再嵌多一层循环,可实现立体点int pt = addpoint(0, set(i, 0, n));
}} 添加copytopoints节点,用立方体box代替点,结果为: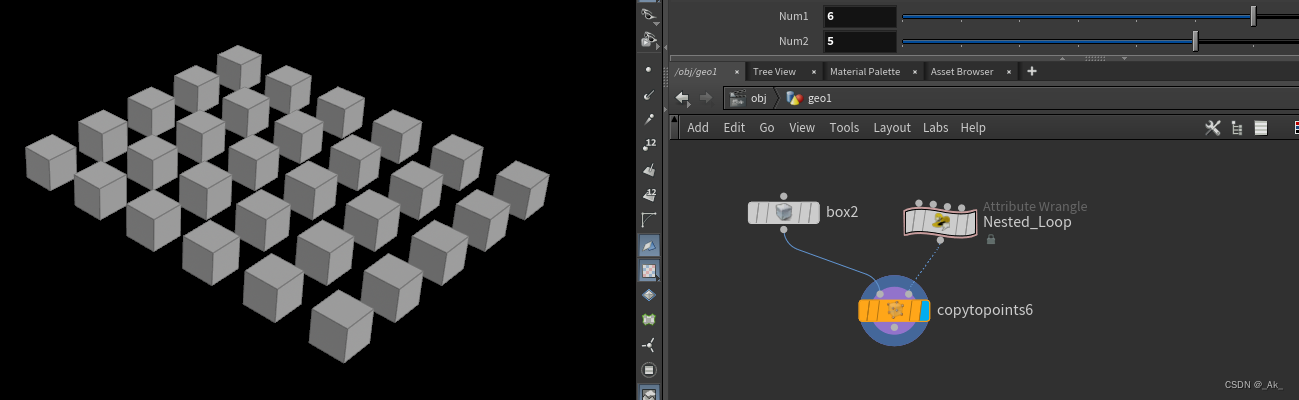
11、嵌套循环与多螺旋曲线
创建单螺旋曲线可查看【3、for循环练习—螺旋曲线】。
创建类型为detail的attributewrangle节点(Exercise4),写入下面代码:
int num1 = chi('num1'); //生成的点数
int num2 = chi('num2'); //生成螺旋线的条数
float angratio = chf('angratio'); //角度系数
float heightratio = chf('heightratio'); //高度系数for(int i=0; i<num1; i++){for(int n=0; n<num2; n++){float stepang = $PI * 2 / num2; //$PI=180°,根据线条数把360°均分作为起点角间隔度float x = cos($PI * angratio * i + stepang * n); //cos(角度+第N条线的角度)float z = sin($PI * angratio * i + stepang * n);float y = i * heightratio;int pt = addpoint(0, set(x, y, z));setpointattrib(0, 'id', pt, n); //给点保存为‘id’属性,根据n来赋值(分组)}
} 添加一个Add节点 ,点击Polygon设置为【ByGroup—>Add:By Attribute—>Attribute Name:id】,结果为:
这篇关于HoudiniVex笔记_P7_Loop循环的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




