本文主要是介绍讲下 V8 sort 的大概思路,并手写一个 sort 的实现,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
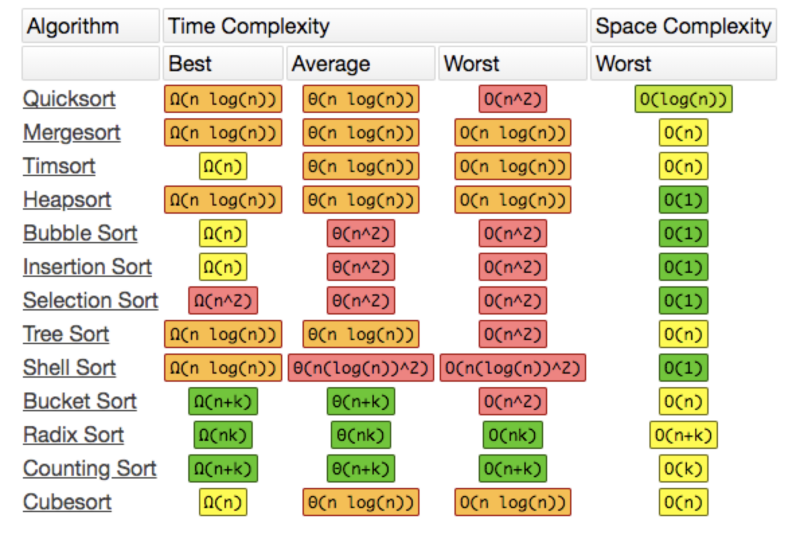
以上是常见的几种排序算法,首先思考一下, Array.prototype.sort() 使用了上面的那种算法喃?
Array.prototype.sort()
sort()方法用原地算法对数组的元素进行排序,并返回数组。默认排序顺序是在将元素转换为字符串,然后比较它们的UTF-16代码单元值序列时构建的— MDN
const array = [1, 30, 4, 21, 100000];
array.sort();
console.log(array);
// [1, 100000, 21, 30, 4]const numbers = [4, 2, 5, 1, 3];
numbers.sort((a, b) => a - b);
console.log(numbers)
// [1, 2, 3, 4, 5]V8 种的 Array.prototype.sort()
关于 Array.prototype.sort() ,ES 规范并没有指定具体的算法,在 V8 引擎中, 7.0 版本之前 ,数组长度小于10时, Array.prototype.sort() 使用的是插入排序,否则用快速排序。
在 V8 引擎 7.0 版本之后 就舍弃了快速排序,因为它不是稳定的排序算法,在最坏情况下,时间复杂度会降级到 O(n2)。
于是采用了一种混合排序的算法:TimSort 。
这种功能算法最初用于Python语言中,严格地说它不属于以上10种排序算法中的任何一种,属于一种混合排序算法:
在数据量小的子数组中使用插入排序,然后再使用归并排序将有序的子数组进行合并排序,时间复杂度为 O(nlogn) 。

什么是 TimSort ?
在 解答 v8 sort 源码前,我们先看看 TimSort 具体是如何实现的,帮助我们阅读源码
Timsort 是 Tim Peter 在 2001 年为 Python 语言特意创造的,主要是 基于现实数据集中存在者大量的有序元素(不需要重新排序) 。 Timsort 会遍历所有数据,找出数据中所有有序的分区(run),然后按照一定的规则将这些分区(run)归并为一个。
具体过程为:
- 扫描数组,并寻找所谓的
_runs_,一个 run 可以认为是已经排序的小数组,也包括以逆向排序的,因为这些数组可以简单地翻转(reverse)就成为一个run - 确定最小 run 长度,小于的 run 会通过 插入排序 归并成长度高于最小长度的 run
- 反复归并一些相邻 run ,过程中避免归并长度相差很大的片段,直至整个排序完成
如何避免归并长度相差很大 run 呢?在 Timsort 排序过程中,会存在一个栈用于记录每个 run 的起始索引位置与长度, 依次将 run 压入栈中,若栈顶 A 、B、C 的长度
|C| > |B| + |A||B| > |A|

在上图的例子中,因为 | A |> | B | ,所以B被合并到了它前后两个runs(A、C)中较小的一个 | A | ,然后 | A | 再与 | C | 。 依据这个法则,能够尽量使得大小相同的 run 合并,以提高性能。注意Timsort是稳定排序故只有相邻的 run 才能归并。
所以,对于已经排序好的数组,会以 O(n) 的时间内完成排序,因为这样的数组将只产生单个 run ,不需要合并操作。最坏的情况是 O(n log n) 。这样的算法性能参数,以及 Timsort 天生的稳定性是我们最终选择 Timsort 而非 Quicksort 的几个原因。
手写一个 Array.prototype.sort() 实现
了解的 Timsort 的基本思想与排序过程后,我们手写一个简易版的 Timsort :
// 顺序合并两个小数组left、right 到 result
function merge(left, right) {let result = [],ileft = 0,iright = 0while(ileft < left.length && iright < right.length) {if(left[ileft] < right[iright]){result.push(left[ileft ++])} else {result.push(right[iright ++])}}while(ileft < left.length) {result.push(left[ileft ++])}while(iright < right.length) {result.push(right[iright ++])}return result
}// 插入排序
function insertionSort(arr) {let n = arr.length;let preIndex, current;for (let i = 1; i < n; i++) {preIndex = i - 1;current = arr[i];while (preIndex >= 0 && arr[preIndex] > current) {arr[preIndex + 1] = arr[preIndex];preIndex--;}arr[preIndex + 1] = current;}return arr;
}// timsort
function timsort(arr) {// 空数组或数组长度小于 2,直接返回if(!arr || arr.length < 2) return arrlet runs = [], sortedRuns = [],newRun = [arr[0]],length = arr.length// 划分 run 区,并存储到 runs 中,这里简单的按照升序划分,没有考虑降序的runfor(let i = 1; i < length; i++) {if(arr[i] < arr[i - 1]) {runs.push(newRun)newRun = [arr[i]]} else {newRun.push(arr[i])}if(length - 1 === i) {runs.push(newRun)break}}// 由于仅仅是升序的run,没有涉及到run的扩充和降序的run,因此,其实这里没有必要使用 insertionSort 来进行 run 自身的排序for(let run of runs) {insertionSort(run)}// 合并 runssortedRuns = []for(let run of runs) {sortedRuns = merge(sortedRuns, run)}return sortedRuns
}// 测试
var numbers = [4, 2, 5, 1, 3]
timsort(numbers)
// [1, 2, 3, 4, 5]简易版的,完整的实现可以查看 v8 array-sort 实现,下面我们就来看一下
v8 中的 Array.prototype.sort() 源码解读
即 TimSort 在 v8 中的实现,具体实现步骤如下:
- 判断数组长度,小于2直接返回,不排序
- 开始循环
- 找出一个有序子数组,我们称之为 “run” ,长度 currentRunLength
- 计算最小合并序列长度 minRunLength (这个值会根据数组长度动态变化,在32~64之间)
- 比较 currentRunLength 和 minRunLength ,如果 currentRunLength >= minRunLength ,否则采用插入排序补足数组长度至 minRunLength ,将 run 压入栈 pendingRuns 中
- 每次有新的 run 被压入 pendingRuns 时保证栈内任意 3 个连续的 run(run0, run1, run2)从下至上满足run0 > run1 + run2 && run1 > run2 ,不满足的话进行调整直至满足
- 如果剩余子数组为 0 ,结束循环
- 合并栈中所有 run,排序结束
核心源码解读
下面重点解读 3 个核心函数:
ComputeMinRunLength:用来计算minRunLengthCountAndMakeRun:计算第一个run的长度MergeCollapse:调整pendingRuns,使栈长度大于3时,所有run都满足run[n]>run[n+1]+run[n+2]且run[n+1]>run2[n+2]
// 计算最小合并序列长度 minRunLength
macro ComputeMinRunLength(nArg: Smi): Smi {let n: Smi = nArg;let r: Smi = 0; // Becomes 1 if any 1 bits are shifted off.assert(n >= 0);// 如果小于 64 ,则返回n(该值太小,无法打扰那些奇特的东西)// 否则不断除以2,得到结果在 32~64 之间while (n >= 64) {r = r | (n & 1);n = n >> 1;}const minRunLength: Smi = n + r;assert(nArg < 64 || (32 <= minRunLength && minRunLength <= 64));return minRunLength;
}// 计算第一个 run 的长度
macro CountAndMakeRun(implicit context: Context, sortState: SortState)(lowArg: Smi, high: Smi): Smi {assert(lowArg < high);// 这里保存的才是我们传入的数组数据const workArray = sortState.workArray;const low: Smi = lowArg + 1;if (low == high) return 1;let runLength: Smi = 2;const elementLow = UnsafeCast<JSAny>(workArray.objects[low]);const elementLowPred = UnsafeCast<JSAny>(workArray.objects[low - 1]);// 调用比对函数来比对数据let order = sortState.Compare(elementLow, elementLowPred);// TODO(szuend): Replace with "order < 0" once Torque supports it.// Currently the operator<(Number, Number) has return type// 'never' and uses two labels to branch.const isDescending: bool = order < 0 ? true : false;let previousElement: JSAny = elementLow;// 遍历子数组并计算 run 的长度for (let idx: Smi = low + 1; idx < high; ++idx) {const currentElement = UnsafeCast<JSAny>(workArray.objects[idx]);order = sortState.Compare(currentElement, previousElement);if (isDescending) {if (order >= 0) break;} else {if (order < 0) break;}previousElement = currentElement;++runLength;}if (isDescending) {ReverseRange(workArray, lowArg, lowArg + runLength);}return runLength;
}// 调整 pendingRuns ,使栈长度大于3时,所有 run 都满足 run[n]>run[n+1]+run[n+2] 且 run[n+1]>run2[n+2]
transitioning macro MergeCollapse(context: Context, sortState: SortState) {const pendingRuns: FixedArray = sortState.pendingRuns;// Reload the stack size because MergeAt might change it.while (GetPendingRunsSize(sortState) > 1) {let n: Smi = GetPendingRunsSize(sortState) - 2;if (!RunInvariantEstablished(pendingRuns, n + 1) ||!RunInvariantEstablished(pendingRuns, n)) {if (GetPendingRunLength(pendingRuns, n - 1) <GetPendingRunLength(pendingRuns, n + 1)) {--n;}MergeAt(n); // 将第 n 个 run 和第 n+1 个 run 进行合并} else if (GetPendingRunLength(pendingRuns, n) <=GetPendingRunLength(pendingRuns, n + 1)) {MergeAt(n); // 将第 n 个 run 和第 n+1 个 run 进行合并} else {break;}}
}最后
本文首发自「三分钟学前端」,回复「交流」自动加入前端三分钟进阶群,每日一道编程算法面试题(含解答),助力你成为更优秀的前端开发! 
这篇关于讲下 V8 sort 的大概思路,并手写一个 sort 的实现的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


