本文主要是介绍(未看完)非配对接送的多次访问的车辆路径问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
- DOI:10.1016/j.tre.2017.04.011
摘要
- 非配对接送的多次访问的车辆路径问题(或者叫做the many-to-many pickup and delivery problem (Battara et al., 2014) with multi-visit)
- 决策:供需配对和车辆路径
- 提出数学模型,采用禁忌搜索算法提出高质量的解决方案
问题背景与文献综述
- 解决烟草公司的工厂之间转移各种原材料运输成本问题。
问题背景
1)每个工厂使用(本地)仓库来储存原材料
2)为确保快速响应和顺利生产,在收到公司中央计划部的10天生产计划后,各工厂需要自行做出工厂间原材料转移决策,以防止缺货。
3)原材料转移方式:当工厂1有发货请求(即需要一定数量的特定类型的原材料)时,它会将发货请求发送到最近的工厂(例如工厂2);收到交付请求后,工厂2将向工厂1交付请求的原材料,车辆将空车返回;如果工厂2无法完全满足工厂1的需求(即供应有限),则将按照距离(到工厂1)的非递减顺序依次选择其他工厂,直到完全满足需求。
4)每个工厂可能需要一种或几种类型的原材料,但能够同时供应其他类型的原材料。
5)在烟草公司目前的转让模式下,决策权是分散的。
-鉴于上述问题,烟草公司已开始建立一个中央物流管理部门,旨在从全球角度解决这一问题。
- 此外,网络中的收货和交货时间窗口可以忽略,因为生产计划提前相当一段时间发布,这给了每个工厂足够的时间来收货和交货原材料,以服务于生产。
文献综述
- 本问题与海上路由和调度问题(MRSP)密切相关。
-MRSP与MIRP类似,但不同之处在于运输与生产无关,因此每种产品的供需信息是确定的。
-与MRSP相比,本研究放宽了收货和发货的时间窗限制,复杂性大大增加。 - 本问题也与未配对取货和交货问题(UPDP)密切相关。UPDP可分为两类。
-其中一类是带单车的UPDP问题,称为接送旅行商问题(PDTSP)。1-PDTSP由Hernández-Pérez和Salazar Gonzalez(2004a)推出。m-PDTSP由Hernández-Pérez和Salazar Gonzalez(2014)提出。
-另一类是多车辆UPDP,称为PDVRP。 - 本问题也与分割配送车辆路径问题(SDVRP)有关。本问题允许一辆车多次拜访客户,即同一辆车或不同的车可以多次拜访客户。显然,问题更复杂,但可以节省更多的运输成本。
问题描述和数学模型建立
问题描述
- 一个包含多个客户、多个产品和一个仓库的运输网络中,具有多个访问的多商品非配对接送车辆路径问题。根据容量和持续时间的限制,分配车队在网络内提取和交付各种产品,以满足每个客户的需求,目标是最小化总运输成本。
- 假设:
1)车辆是同质的,即所有车辆具有相同的容量、最大工作时间和恒定的行驶速度。
2)每个客户的装卸时间可以忽略不计
3)对于每个客户,每种产品的供应都是有限的。该假设基于实际情况,因为每个工厂的存储容量有限,库存会产生库存持有成本。
4)对于每种产品,总供应量不低于总需求量。
5)对于每个客户,其总需求可以通过多次交付相同或不同的车辆来满足;但是,不允许对同一类型的产品进行分批交付。这个假设是基于现实的。通过一次交货满足对同一类型原材料的需求 - N={0,1,…,N,N+1}为顶点集。0和n+1分别代表出发站和目的站,其他顶点表示客户。
- H={1,…,M}是一组产品类型。
- V={1,…,K}是一组可用的交通工具。
- cij是顶点i和j之间的对称旅行费用,等于这两个顶点之间的旅行距离,遵循三角形不等式原理。
- tij为i和j之间的行驶时间,等于cij与车速之比。
- Q为车辆容量,T为车辆的最大工作时间。
数学模型
- (值得学习写作的部分,可纳入论文)即使对于客户数为7、产品类型数为2的问题,基

本模型也很难获得最优解(参见表2)。基本模型非常复杂,主要有两个原因。
1)变量维数过多:放松了单次访问假设,这导致决策变量是高维的(即,路线决策变量是五维的,取送数量决策变量是四维的)。
2)每个顶点的访问次数事先是未知的。在测试中,每个顶点的访问时间上限必须设置为足够大的数量(即总供应量加上顶点处的需求产品类型数量),以获得全局最优解。 - 因此,基本模型basic model不适用于所研究的问题,并提出了“统一”模型unify model作为简化。由于基本模型能更直观地反映调查问题,从而帮助不同研究背景的读者更清楚地理解问题及其复杂性
Basic model
-
问题描述为网络(i, a),i即节点,a即第a次访问


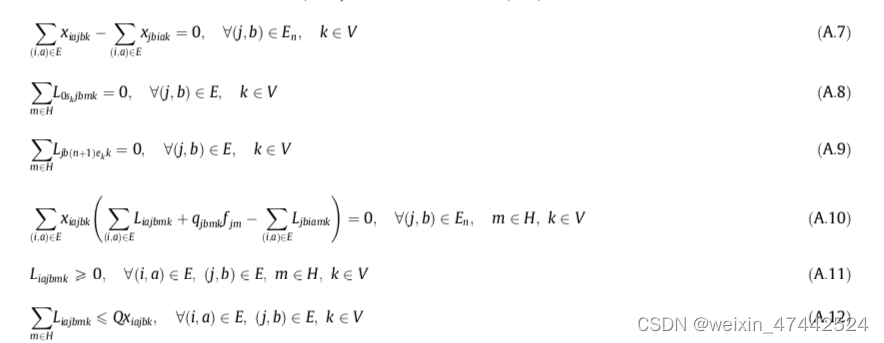
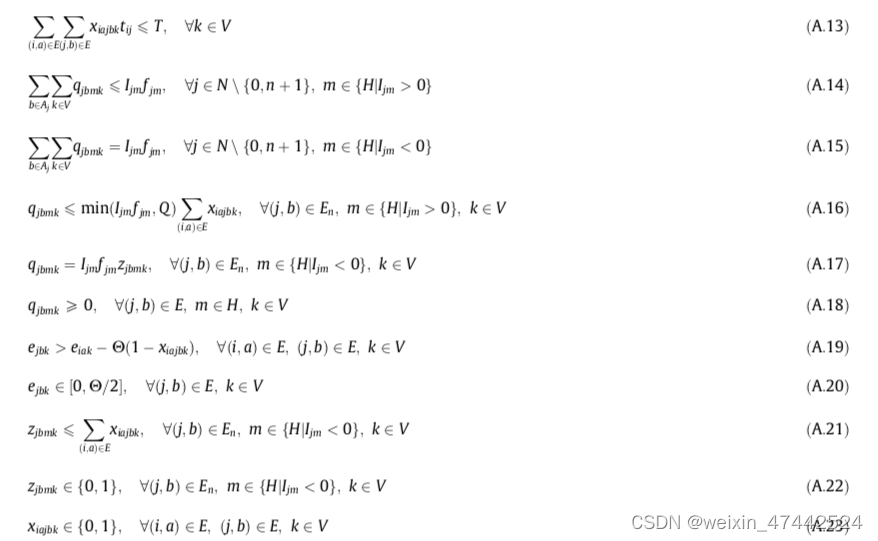
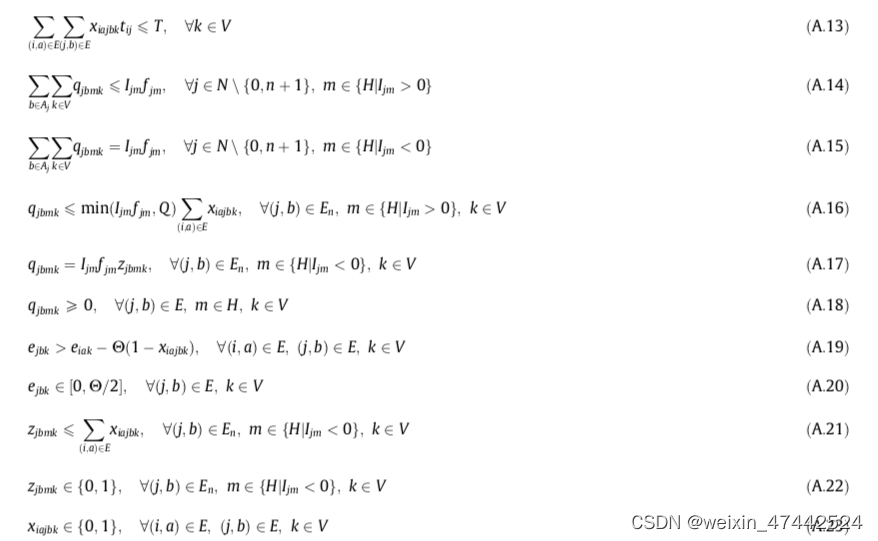
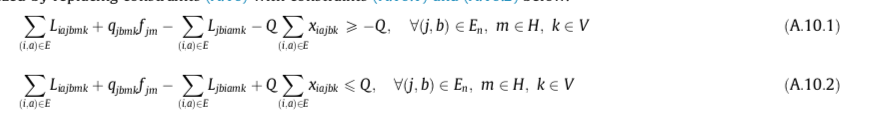
-
MIP相关含义
A.1:最小化成本
A.2-A.5:确保每辆车从出发车辆段出发2和3,并在目的地车辆段终止4和5。3和5保证车辆仅执行一次行程。
A.6:表示每个位置 (j,b) 仅访问一次
A.7:确保流量守恒
A.8:确保空车出发
A.9:空车返回
A.10:确保如果车辆k到达(j,b),到达(j,b)时车上产品m的数量加上或减去(j,b)处产品m的交付数量,等于车辆离开(j,b)时车上产品m的数量。
A.11:路线中任意两个位置之间的任何产品的装载量不小于零
A.12:规定不能超过每辆车的容量
A.13:确保每辆车的行驶时间不超过其最大工作时间
A.14:如果j是产品m的供应顶点,则顶点j处产品m的供应其他点点总量不超过供应量。
A.15:如果j是产品m的需求顶点,则顶点j处产品m的总交付量等于需求量。
A.16:如果j是产品m的供应顶点,则位置(j,b)处产品m的拾取量不大于顶点j处产品m的供应量和车辆容量中的较小者。并且车辆k未访问(j,b),则qjbmk为0
A.17:如果j是产品m的需求顶点,位置(j,b)处产品m的交付量将等于顶点j处产品m的需求量或等于零。
A.18:收货/发货数量非负
A.19和A.20:消除了每条路线的子路线,MTZ约束
A.21:z与x的关系
A.22和A.23:决策变量的约束
!!!(可学习的转换)A.10替换为A10.1和A.10.2,非线性——线性
Unify model
- 主要思想是顶点分割。为了避免混淆,使用“节点”来表示从原始顶点分割的子顶点。即使用nodes代替sub-vertexs
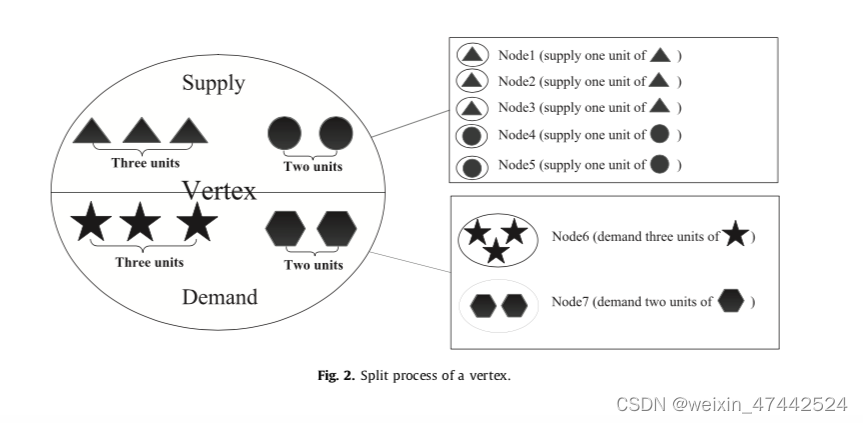
- 根据每个顶点的供需信息,将其分为一组或两组与顶点坐标相同的节点。一种是供应节点组,其中每个节点仅供应一种产品,供应数量为一个单位。因此,供应节点的数量等于在原始顶点供应的所有产品的总量。另一个是需求节点组,其中一个节点表示对一种产品类型的需求

- 1:最小化总费用

- 2-5:保证车辆从depot出发一次,结束一次


- 6-7 :每个节点访问小于等于一次的约束,⚠️demand和supply的区别

- 8:流量守恒约束(针对1…nu,因为前面对depot进行限制)

- 9-12:载重约束。9和10对起始和结束进行约束,11对过程中车辆载重进行计算,12对行程中载重的限制

- 13:最大行驶时间约束

- 14-15:子循环约束<参考的 Miller et al. (1960) and Bektas (2006)>
 - 15:变量类型约束
- 15:变量类型约束
- 18-:pickup and delivery 约束
!!统一模型的解空间比基本模型的解空间大,因为基本模型中的每种产品类型都被视为一个整体,并且一次从一个供应点获取。
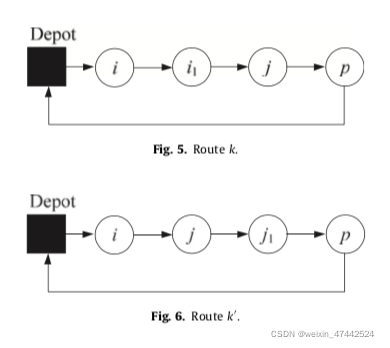
该解空间会出现交叉情况crossed pickup,如下图所示。因此增加相关约束,保证与basic model的解空间相同。
18:不同类型的交付不能出现交叉,即相同类型的产品应该一起挑选。
19-21:保证当在一个顶点获取/交付多种类型的产品时,只有一个序列执行获取/交付操作。19保证当需要在一个顶点pickup多种类型的产品时,pickup从小索引产品开始(20则针对delivery)。21确保当pickup和delivery操作都应在顶点执行时,首先执行delivery操作。
22:如果访问某个顶点时需要pickup多个产品单元,则pickup从节点索引较小的节点开始。



- 统一模型具有更少的决策变量和约束;路由决策变量的维数减少到3,pickup/delivery数量决策变量被消除。
!!Valid inequalities
- 在统一模型下,即使对于客户数为9、产品类型数为2的问题,也无法获得最优值或更严格的下限(参见表2)。为了确保在时间限制内或内存不足之前从CPLEX中得到最优值或更严格的下限,提出了一些有效的不等式来加强统一模型。
Symmetry breaking inequalities
- Symmetry breaking for solutions:解决不同路线但成本相同——采用改进目标函数引入 min load *distance即LD,如23所示。其中p为参数,可看原文取值,小于0.01

- Symmetry breaking inequalities for vehicle index:使用指数更小的车辆

- Symmetry breaking inequalities for homogeneous node index(对于同质节点的约束)
1)25:对于同质supply节点选择更小index的节点进行服务
2)26:如果同一车辆访问两个同质supply节点,则会按照节点索引的非降序访问。即索引较小的节点具有被访问的优先级。
3)27:如果两个同质supply节点被不同的车辆访问,则索引较小的节点被索引较小的车辆访问
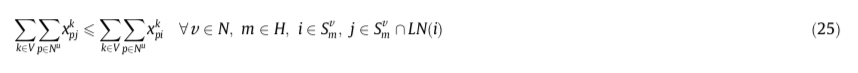
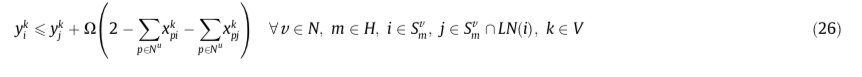
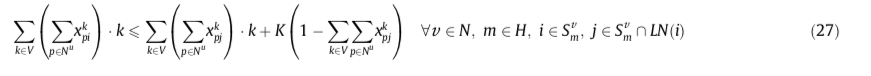
Three nodes sub-route elimination inequalities
- 可行路线应满足的四个条件:(a)每种产品的提货量等于交货量;(b) 每个需求节点的需求必须通过一次访问来满足,这符合不允许在每个顶点对同一类型的产品进行拆分交付的假设;(c) 任意两个节点之间的负载量为非负且不超过车辆容量;(d) 路线的持续时间不超过车辆的最大工作时间。
- 命题:
- 具有多仓库的SDVRP(Gulczynski等人,2011年;Ray等人,2014年;Wang等人,2016年)和具有商品约束的SDVRP(Archetti等人,2015年)
这篇关于(未看完)非配对接送的多次访问的车辆路径问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





