CodeForces 742B Arpa’s obvious problem and Mehrdad’s terrible solution

本文主要是介绍CodeForces 742B Arpa’s obvious problem and Mehrdad’s terrible solution，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

There are some beautiful girls in Arpa’s land as mentioned before.

Once Arpa came up with an obvious problem:

Given an array and a number x, count the number of pairs of indices i, j (1 ≤ i < j ≤ n) such that 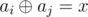$\text{[math]}$ , where $\text{[math]}$ is bitwise xor operation (see notes for explanation).

$\text{[math]}$

Immediately, Mehrdad discovered a terrible solution that nobody trusted. Now Arpa needs your help to implement the solution to that problem.

Input

First line contains two integers n and x (1 ≤ n ≤ 10⁵, 0 ≤ x ≤ 10⁵) — the number of elements in the array and the integer x.

Second line contains n integers a₁, a₂, ..., a_n (1 ≤ a_i ≤ 10⁵) — the elements of the array.

Output

Print a single integer: the answer to the problem.

Examples

Input

2 3
1 2

Output

Input

6 1
5 1 2 3 4 1

Output

Note

In the first sample there is only one pair of i = 1 and j = 2. 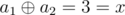$\text{[math]}$ so the answer is 1.

In the second sample the only two pairs are i = 3, j = 4 (since 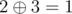$\text{[math]}$ ) and i = 1, j = 5 (since $\text{[math]}$ ).

A bitwise xor takes two bit integers of equal length and performs the logical xor operation on each pair of corresponding bits. The result in each position is 1 if only the first bit is 1 or only the second bit is 1, but will be 0 if both are 0 or both are 1. You can read more about bitwise xor operation here: https://en.wikipedia.org/wiki/Bitwise_operation#XOR.

题目给出n个数，以及一个x，求那个数中有几对数可以异或为x；把每对数都异或一遍就T了；那么，怎么做呢？

异或运算有个性质：a^b=c->a^c=b->c^b=a;所以把n个数扫一遍就可以了；

代码如下：

#include <iostream>
#include <algorithm>
#include <string.h>using namespace std;long long a[100005];
long long b[200006];   //要开两倍，否则会WA；
int main(){long long n, x;long long cnt=0;cin >> n >> x;memset(b, 0, sizeof(b));for(int i=1; i<=n; i++){cin >> a[i];b[a[i]]++;}for(int i=1; i<=n; i++){long long c=x^a[i];cnt+=b[c];                //有几个c结果就加几；if(a[i]==c) cnt--;        //如果a[i]==c;就减去自身；}cout << cnt/2;                //每个数都与x异或一遍，如x=3时，1^2=3,2^1=3,但其实是一样的，每对数return 0;                     //都重复找了两遍，所以要/2；
}