NOIP2016D1T2-天天爱跑步

问题描述

小c同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。《天天爱跑步》是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。
这个游戏的地图可以看作一一棵包含 n 个结点和 n-1 条边的树, 每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从 11 到 nn 的连续正整数。
现在有 m 个玩家,第 ii 个玩家的起点为 Si,终点为 Ti。每天打卡任务开始时,所有玩家在第 0 秒同时从自己的起点出发, 以每秒跑一条边的速度, 不间断地沿着最短路径向着自己的终点跑去, 跑到终点后该玩家就算完成了打卡任务。 (由于地图是一棵树, 所以每个人的路径是唯一的)
小c想知道游戏的活跃度, 所以在每个结点上都放置了一个观察员。 在结点 jj 的观察员会选择在第 Wj秒观察玩家, 一个玩家能被这个观察员观察到当且仅当该玩家在第Wj秒也理到达了结点 j 。 小C想知道每个观察员会观察到多少人?
注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏, 他不能等待一 段时间后再被观察员观察到。 即对于把结点 j 作为终点的玩家: 若他在第 Wj秒前到达终点,则在结点 j 的观察员不能观察到该玩家;若他正好在第 Wj秒到达终点,则在结点 j 的观察员可以观察到这个玩家。
输入格式
第一行有两个整数 n 和 m 。其中 n 代表树的结点数量, 同时也是观察员的数量, m 代表玩家的数量。
接下来 n- 1 行每行两个整数 u 和 v ,表示结点 u 到结点 v 有一条边。
接下来一行 n 个整数,其中第 j个整数为Wj,表示结点 j 出现观察员的时间。
接下来 mm 行,每行两个整数 Si,和Ti,表示一个玩家的起点和终点。
对于所有的数据,保证 1≤Si,Ti≤n,0≤Wj≤n。
输出格式
输出1行 n 个整数,第 j 个整数表示结点 j 的观察员可以观察到多少人。
样例输入

6 3
2 3
1 2 
1 4 
4 5 
4 6 
0 2 5 1 2 3 
1 5 
1 3 
2 6 

样例输出

2 0 0 1 1 1 

思路分析

首先我想的是暴力，那路径如何确定呢，一开始只想到这种情况暴力

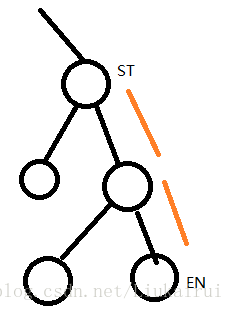
于是路径就是en->en/2->en/2/2->en/2/2/2->……->st
然后说不对

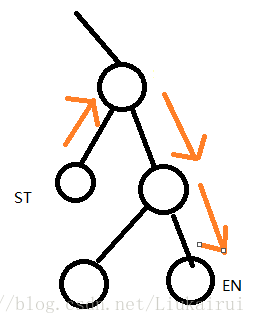
炸了，只能用LCA。。。于是找到最近公共祖先以后然后继续暴力，当然炸了，蒟蒻就想到这里
标准算法：
先把树进行lca，路径分为向上和向下走

1、对于向上走的路径，在i节点，当deep[i]+w[i]==deep[S]时才会产生贡献

借用以T为根节点的思想，开一个桶来差分统计就好了

2、对于向下走的路径，在i节点，当deep[i]-w[i]==deep[T]-dis[S,T]-pret[T]时才会产生贡献【dis表示路径长，pret表示若该路径起点为lca,则走到lca时是什么时刻，若该路径起点为自然起点，则pret=0】

3、进行同样的统计，到i节点时把向上路径的起点S_up和向下路径的终点T_up【起点在上面的终点】的对应的bac[ ]++【例如T_up就是bac[deep[T]-dis[S,T]-pret[T]]++】，在访问结束时将向下路径的起点S_down和向上路径的终点T_up对应的另一个端点的统计撤销【类似于链状部分分的算法，看不明白可以参照一下】

4、若该点为lca且该点产生了贡献，贡献值应该-1，因为统计了两次
蒟蒻不会…

AC代码

//抄的洛谷的
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#define LL long long int
using namespace std;
const int maxn=700005,maxm=2000100,INF=2000000000,P=1000000007;
//快速读入
inline int read(){int out=0,flag=1;char c=getchar();while(c<48||c>57) {if(c=='-') flag=-1;c=getchar();}while(c>=48&&c<=57){out=out*10+c-48;c=getchar();}return out*flag;
}
//边信息建立
int head[maxn],nedge=0;
struct EDGE{int to,next;
}edge[maxm];
inline void build(int a,int b){edge[nedge]=(EDGE){b,head[a]};head[a]=nedge++;edge[nedge]=(EDGE){a,head[b]};head[b]=nedge++;
}
//lca询问信息建立
int Head[maxn],nlca=0;
struct LCA{int to,flag,next;
}Lca[maxm];
inline void link(int a,int b){Lca[nlca]=(LCA){b,0,Head[a]};Head[a]=nlca++;Lca[nlca]=(LCA){a,0,Head[b]};Head[b]=nlca++;
}
int N,M,w[maxn],rt=0,Siz[maxn],disrt=INF;
//数据读入
void init(){fill(head,head+maxn,-1);fill(Head,Head+maxn,-1);N=read();M=read();int a,b;for(int i=1;i<N;i++) build(read(),read());for(int i=1;i<=N;i++) w[i]=read();for(int i=1;i<=M;i++){a=read();b=read();link(a,b);}
}
//重心为根
void dfs1(int u,int f){int to,Min=INF,Max=-INF;Siz[u]=1;for(int k=head[u];k!=-1;k=edge[k].next)if((to=edge[k].to)!=f){dfs1(to,u);Siz[u]+=Siz[to];if(Siz[to]<Min) Min=Siz[to];if(Siz[to]>Max) Max=Siz[to];}if(Min==INF) return;if(N-Siz[u]<Min&&f) Min=N-Siz[u];if(N-Siz[u]>Max) Max=N-Siz[u];if(Max-Min<disrt){disrt=Max-Min;rt=u;}
}
void focus(){dfs1(1,0);if(!rt) rt=1;//cout<<rt<<endl;
}
vector<int> Su[maxn],Sd[maxn],Tu[maxn],Td[maxn];
int pre[maxn],dep[maxn],dis[maxn],S[maxn],T[maxn],pret[maxn],pathi=0,temp;
int lca0[maxn];
bool vis[maxn];
inline int find(int u){return u==pre[u] ? u:pre[u]=find(pre[u]);
}
//tarjan_lca算法割路径
void dfs2(int u,int f){int to;pre[u]=u;dep[u]=dep[f]+1;vis[u]=true;for(int k=head[u];k!=-1;k=edge[k].next){if((to=edge[k].to)!=f){dfs2(to,u);pre[to]=u;}}for(int k=Head[u];k!=-1;k=Lca[k].next){if(!Lca[k].flag&&vis[to=Lca[k].to]){Lca[k].flag=Lca[k^1].flag=true;int flag=0,m=find(to);if(!(k&1)) {flag=1;to^=u^=to^=u;}pathi++;if(to==m){S[pathi]=to;T[pathi]=u;dis[pathi]=dep[u]-dep[to];pret[pathi]=0;Sd[to].push_back(pathi);Tu[u].push_back(pathi);}else if(u==m){S[pathi]=to;T[pathi]=u;dis[pathi]=dep[to]-dep[u];Td[u].push_back(pathi);Su[to].push_back(pathi);}else{lca0[pathi]=m;S[pathi]=to;T[pathi]=m;dis[pathi]=dep[to]-dep[m];Su[to].push_back(pathi);Td[m].push_back(pathi);S[++pathi]=m;T[pathi]=u;dis[pathi]=dep[u]-dep[m];pret[pathi]=dep[to]-dep[m];Sd[m].push_back(pathi);Tu[u].push_back(pathi);}if(flag) u=to;}}
}
void tarjan_lca(){dfs2(rt,0);/*for(int i=1;i<=pathi;i++){printf("%d %d %d\n",S[i],T[i],dis[i]);}*/
}
int cntS[maxm],cntT[maxm],ans[maxn];
//树上统计
void dfs(int u,int f){int dS=dep[u]+w[u]+maxn,oriS=cntS[dS],dT=dep[u]-w[u]+maxn,oriT=cntT[dT],to;for(unsigned i=0;i<Su[u].size();i++){cntS[dep[S[Su[u][i]]]+maxn]++;}for(unsigned i=0;i<Tu[u].size();i++){cntT[dep[T[Tu[u][i]]]-dis[Tu[u][i]]-pret[Tu[u][i]]+maxn]++;}for(int k=head[u];k!=-1;k=edge[k].next){if((to=edge[k].to)!=f){dfs(to,u);}}ans[u]=cntS[dS]-oriS+cntT[dT]-oriT;for(unsigned i=0;i<Td[u].size();i++){cntS[dep[S[Td[u][i]]]+maxn]--;//if(u==2) cout<<"lca:"<<lca0[Td[u][i]]<<endl;if(lca0[Td[u][i]]==u&&dep[S[Td[u][i]]]+maxn==dS) ans[u]--;}for(unsigned i=0;i<Sd[u].size();i++){cntT[dep[T[Sd[u][i]]]-dis[Sd[u][i]]-pret[Sd[u][i]]+maxn]--;}
}
//打印答案
void print(){printf("%d",ans[1]);for(int i=2;i<=N;i++) printf(" %d",ans[i]);printf("\n");
}
int main(){init();focus();tarjan_lca();dfs(rt,0);print();return 0;
}