代码本色学习之漂亮的球球在哪里

本文主要是介绍代码本色学习之漂亮的球球在哪里，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在本学期的末尾，老师让我们根据《代码本色》这本书包括引言在内的前四章进行示例编程。并且写出一篇博文，下面，让我来介绍一下它们。
（因为是对每一个示例分板块进行介绍，板块中有重复使用的功能，我就不在每一个板块都进行重复说明了）

一、了解“代码本色”

本书介绍了用计算机模拟自然系统涉及的编程策略与技术，涵盖了基本的数学和物理概念，以及可视化地展示模拟结果所需的高级算法。

二、示例学习

1、第0章 引言

1.1、示例展示

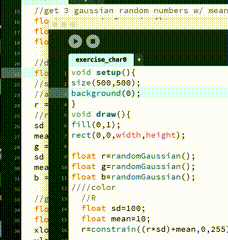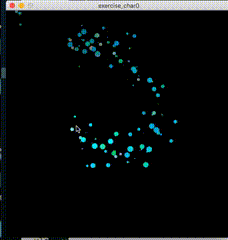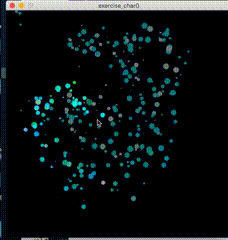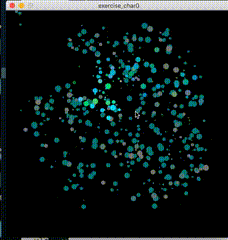
1.2、原理

原理：
一、色彩范围
在ps中选取RGB(10,235,235);当仅对b值进行修改时，其取色范围：

仅对g值进行修改K：

仅对r值进行修改：

因此在近似值中进行取色，得到的效果就是上图所示，颜色搭配起来很舒适的同色系或相近色系的色彩。
二、随机取数
1、random（x）
x是随机取数的范围。在本例中，用到random（）取样的只有随着鼠标拖动生成的圆点的半径大小。

float radius;
radius=random(13);
ellipse(xloc,yloc,radius,radius);

2、randomGaussian（）
会返回一个在0-1之间的浮点数
2.1应用于颜色选取：

float r=randomGaussian();
float g=randomGaussian();
float b=randomGaussian();
color//Rfloat sd=100;float mean=10;r=constrain((r*sd)+mean,0,255);//Gsd=10;mean=225;g=constrain((g*sd)+mean,0,255);//Bsd=50;mean=235;b=constrain((b*sd)+mean,0,255);

2.2应用于位置选取
为了使得有原点在鼠标拖动时生成在鼠标点击的附近，同样使用了随机参数。

float xloc=randomGaussian();
float yloc=randomGaussian();sd=20;
xloc=(xloc*sd)+mouseX;
yloc=(yloc*sd)+mouseY;

三、固定范围
constrain（）
constrain（a，b，c）
将a的取值范围限制在b和c之间，如果小于b则取b，大于c则取c。

2、第1章 向量

2.1示例展示

2.2原理

一、随着鼠标距离变化的颜色和圆圈大小

void colors(int i){
float r=randomGaussian();
float g=randomGaussian();
float b=randomGaussian();
color//Rfloat sd=10;float mean=123;r=constrain((r*sd)+mean,0,255);//Gsd=10;mean=207;g=constrain((g*sd)+mean,0,255);gg[i]=g;//Bsd=10;mean=246;b=constrain((b*sd)+mean,0,255);bb[i]=b;
ccolor=color(r,gg[i],bb[i]);
}void changecolor(Mover move,int ii){
dis=abs(dis);
move.ccolor=color(dis,gg[ii],bb[ii]);
//println(dis);
}

在ps中颜色的取值：

随着鼠标和圆圈距离的改变，所取颜色的r值也在改变，于是有了蓝色粉色渐变的效果，而圆圈大小的改变也是这个原理。
二、Mover类
类中的变量：

  PVector position;//位置PVector velocity;/速度PVector acceleration;//加速度float topspeed;//最大速度color ccolor;//颜色

构造函数：

  Mover() {// Start in the centerposition = new PVector(random(width),random(height));velocity = new PVector(0,0);topspeed = 5;}

速度位置计算：
计算加速度：
设置鼠标位置为向量点：

PVector mouse = new PVector(mouseX,mouseY);

加速度：mover当前位置点指向鼠标位置：

acceleration = PVector.sub(mouse,position);

计算速度方向和加速度：

acceleration.normalize();//单位华只剩方向
acceleration.mult(0.2);//加速度大小设置为0.2

速度的变化以及位置的变化：

velocity.add(acceleration);//速度变化
velocity.limit(topspeed);//速度大小限制
position.add(velocity);//位置变化

边缘检测：
如果碰到边缘，速度方向取反，位置变为碰撞处，有弹跳效果。

void checkEdges(int i) {if (position.x > width) {position.x = width;velocity.x *= -1*i;} else if (position.x < 0) {velocity.x *= -1*i;position.x = 0;}if (position.y > height) {velocity.y *= -1*i;position.y = height;}else if(position.y<0){velocity.y *= -1*i;position.y= 0;}}

三、Mover类的示例化：
其实只是说明一下类的示例化，在主类中调用方法是这样做的。

Mover[] movers = new Mover[15];
void setup() {size(640,360);for (int i = 0; i < movers.length; i++) {movers[i] = new Mover(); movers[i].colors(i);}
}void draw() {background(255);for (int i = 0; i < movers.length; i++) {movers[i].update();movers[i].changecolor(movers[i],i);movers[i].display();movers[i].checkEdges(i);    
}
}

3、第2章 力

3.1 示例展示

3.2原理

在本例中，设置了两个力：吸引力和水中的阻力，也用到了力的累加。
颜色变化以及形状变化在前面已经讲过了就不再赘述了。
一、力：
在自然界中，力是一个向量，而表达在processing中，也是一个向量，我们可以通过自定义向量的方式来创造力。
1、吸引力
在现实生活中，我们对于引力 的计算，都是F=Gm1m2/r*r，G为引力常量。
在processing中，我们可以模拟这个公式。为了简化，G的值是我们自定义的一个数，而r则是物体位置的距离大小。

//通过向量相减算两个物体之间的距离
PVector force=PVector.sub(position,m.position);
//取求得向量的大小float d=force.mag();//为了防止物体相隔太远或太近导致距离过大然后算的力趋于无限小或无限大，//所以把力限制在一个固定的范围之内。d=constrain(d,5.0,15.0);
//取方向的方向force.normalize();//求力，G为自定义的引力常量
float strength=(G*mass*m.mass)/(d*d);
//力的大小和方向结合
force.mult(strength);
return force;

2、水里的阻力（流体阻力）
在代码本色中，有讲到简化的阻力：
阻力=速度的平方*阻力系数。
在processing中，阻力系数是由我们自己定义的，而阻力方向则是物体运动方向的反方向。

PVector drag(Mover m) {float speed = m.velocity.mag();//获得速度大小float dragMagnitude = c * speed * speed;//获得进入流体的物体的速度PVector dragForce = m.velocity.get();dragForce.mult(-1);//速度方向取反//速度方向单位化dragForce.normalize();//速度大小和方向结合dragForce.mult(dragMagnitude);return dragForce;}

二、类：主类、移动的小球Mover类、有吸引力的球Attractor类和Liquid类
主类：
主类用于示例化。
并且有一个力的传递，即在attracter类中计算得到的引力会在主类中通过调用mover类对象的方法来进行力的添加

for(int i=0;i<10;i++){
PVector force = a.attract(m[i]);m[i].applyForce(force);m[i].update();...
}

流体阻力同理：

if (liquid.contains(m[i])) {// 计算流体阻力PVector dragForce = liquid.drag(m[i]);// 把阻力加给物体m[i].applyForce(dragForce);}

引力类：
可以通过鼠标点击的方式移动位置，鼠标经过或者点击的时候，该物体的颜色都会发生改变。
计算引力。
流体类：
流体的原理是在画布上进行一个区域的绘制，并且判断是否有物体进入流体，如果进入，则给这个物体施加相应的阻力。
计算阻力。

三、牛顿第二定律的五大特性：

瞬时性：牛顿第二运动定律是力的瞬时作用效果，加速度和力同时产生、同时变化、同时消失。
矢量性： F=ma是一个矢量表达式，加速度和合力的方向始终保持一致。
独立性：物体受几个外力作用，在一个外力作用下产生的加速度只与此外力有关，与其他力无关，各个力产生的加速度的矢量和等于合外力产生的加速度，合加速度和合外力有关。
因果性：力是产生加速度的原因，加速度是力的作用效果h故力是改变物体运动状态的原因。
等值不等质性：虽然 ，但 F=ma不是力，而是反映物体状态变化情况的；虽然 m=F/a，仅仅是 度量物体质量大小的方法，m与F或a无关。
在对物体的速度进行叠加的时候，需要考虑牛顿定律原则。

四、合力与加速度
合力–>加速度
因为力是向量，所以每次有新的力加入时，都使用向量相加的方式来求得合力。而根据牛顿定律可以得到，物体的加速度是物体所受合力除以物体的质量，所以可以先把加速度求出来，再求合加速度。

void applyForce(PVector force) {//求加速度PVector f = PVector.div(force,mass);//合加速度acceleration.add(f);
}

加速度&速度
因为力对物体的作用是瞬时的，所以每一帧物体所受的合力都要重新计算再重新清零。否则则会造成加速度的叠加，然后物体的速度递增。

void update() {
//速度根据加速度增大velocity.add(acceleration);//位置根据速度变化position.add(velocity);//加速度清零重新计算acceleration.mult(0);
}

4、第3章 震荡

4.1示例展示

4.2原理

一、力
1、弹簧弹力
胡克定律：
弹簧的弹力与弹簧的伸长量成正比，数学表示：F=-k*x；（k为弹力常量）。
而在processing中，假设把弹簧正挂，将一个小球拴在上面（无重力），做上下运动，整个系统不受任何其他外力的影响，我们可以通过用正弦函数来模拟整个运动过程。
然而，当有其他外力加在系统上之后，就不能再用该方法来模拟运动了，只能用向量模拟弹力作用了。

弹力的模拟过程：

 PVector force = PVector.sub(b.position, anchor);// 计算拉长后的总长float d = force.mag();//形变量大小float stretch = d - len;// 根据胡克定律对弹力进行计算force.normalize();force.mult(-1 * k * stretch);//力的大小b.applyForce(force);

在本实验中，弹簧的模拟是通过小球位置变化实现的。eg：当我们用鼠标拖动小球，给小球施加力，小球位置发生变化，然后促使弹簧在形变之后再产生一个弹簧看力，从而继续附加给小球。
鼠标拖动小球位移的方法：

  void clicked(int mx, int my) {//传入的是鼠标的位置float d = dist(mx,my,position.x,position.y);//计算鼠标位置和当前物体的距离if (d < mass) {//如果距离小于半径则说明鼠标在拖动小球dragging = true;dragOffset.x = position.x-mx;dragOffset.y = position.y-my;}}

2、重力
在实例化物体的时候，就已经给物体加上了重力。所以当物体被牵扯运动时，所受的力不仅有弹簧的拉力还有重力。

PVector gravity = new PVector(0,2);//模拟重力的向量

3、空气摩擦力—>运动速度的衰减
因为物体在运动的时候还受到周围环境的影响，收到空气的摩擦力，所以运动并不能一直维持下去。要设定一个衰减值用来模拟运动的衰减。

 float damping = 0.98;....void update() { ....velocity.mult(damping);//速度随时间减少....}

二、弹簧类
弹簧类里的初始变量包括：弹簧位置、弹簧固定点以及弹性系数。
方法：构造方法、绑定物体（用于给物体施加力）方法、维持弹簧长度的方法。

用于绑定物体的方法：

 void connect(Bob b) {//计算力，把力施加给绑定的物体PVector force = PVector.sub(b.position, anchor);float d = force.mag();float stretch = d - len;force.normalize();force.mult(-1 * k * stretch);b.applyForce(force);forrce=force;forrce.mult(-0.1);}

维持弹簧长度的方法：
因为弹簧是有形变系数的，挤压到一定程度或者拉伸到一定程度都会造成无法逆转的形变，而在本例中我们使用了constain（）方法对弹簧的长度进行限制，有一部分是符合自然规律，也有一部分是因为弹簧过长或过小都会使得弹力过小或过大

//当弹簧过大或过小的时候都会恢复原长，并且把施加给物体的力清零
void constrainLength(Bob b, float minlen, float maxlen) {PVector dir = PVector.sub(b.position, anchor);float d = dir.mag();if (d < minlen) {dir.normalize();dir.mult(minlen);b.position = PVector.add(anchor, dir);b.velocity.mult(0);} else if (d > maxlen) {dir.normalize();dir.mult(maxlen);b.position = PVector.add(anchor, dir);b.velocity.mult(0);}

5、第4章 粒子系统

5.1示例展示

带背景图片：

不带背景图片：

5.2原理

因为响应鼠标事件使得物体颜色改变，以及物体颜色随着时间和距离的变化已经在上面陈述过了，就不再在这个板块进行过多赘述啦。
一、粒子系统和粒子
我理解的粒子和粒子系统就像是一个装满各式各样的爆米花桶。
固定住的是爆米花的类型是炸米花，但是在实例化的过程中通过随机函数的取值导致出来的粒子从大小到颜色到位置都是无法确定的。“bong！”的一声，爆米花就从桶里出来啦。就像我做的礼物盒。
粒子系统适用于描述复杂系统
两种粒子：
圆形粒子+三角形粒子。
圆形粒子：
随机生成圆形，颜色范围固定
三角形粒子：
随机生成三角形，三角形旋转角度随机，颜色范围固定。
粒子系统：
用于生成、添加和发射粒子。
二、Arraylist
arraylist的功能数组基本上可以实现，但是数组非常麻烦，尤其是对这种单个粒子数目巨大的粒子存储而言。而arraylist本身有函数可以调用，比较方便。
但是要注意粒子在序列的排入和排出方式：

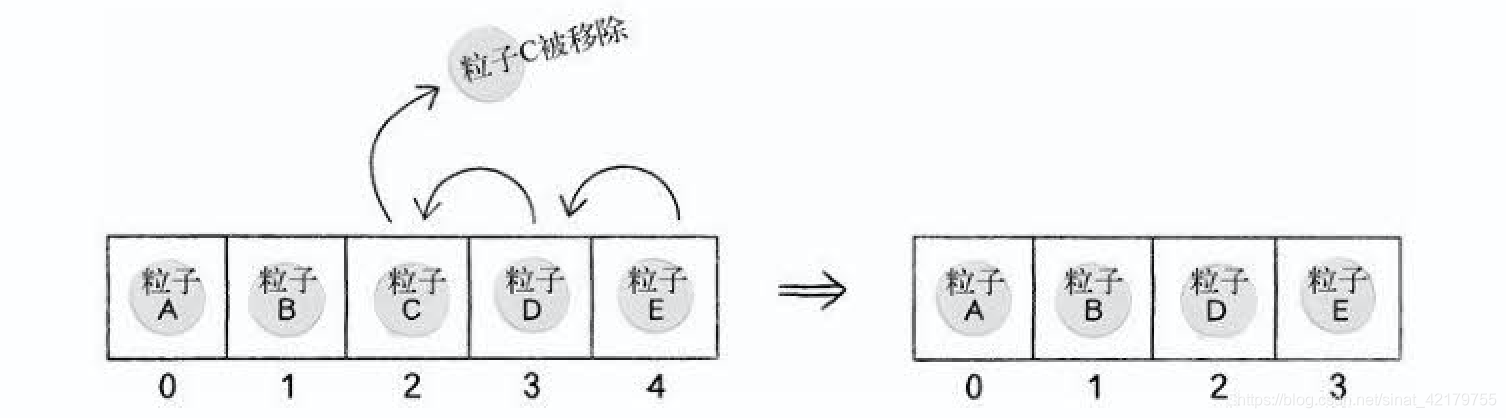
三、粒子色彩的衰减
使用alpha通道，每个被实例化的粒子的颜色随着时间而逐渐变得透明。

  fill(10 + lifespan * 1.2,360, 360, alpha);

同样设置了粒子的存活时间长短，随着lifespan的衰减，粒子的大小也减小，逐渐消失。

四、载入照片做背景图片
将想要用的图片放入项目文件目录之下（注意图片大小和自己设定的画布大小相同）

void setup() {img=loadImage("Yongi.png");size(700, 700);......
}
void draw() {background(img);...
}

三、感悟

在完成本次实验之后，我完成了对《代码本色》这本书前四章和序言的阅读，以及对使用代码语言对自然中规律的一些模拟有了一些了解。其中最让我感兴趣的一句话是当书本说到对重力的模拟时，讲到常量G，说在processing中，我们不使用原本的常量值，而是用1去代替。这是我第一次意识到在可视化模拟编程中对自然系统的模拟的“随心”，往后在模拟弹力，模拟碰撞力，模拟空气摩擦力对速度的作用，都纷纷体现了这种“随意”。在我看来，这中模拟方式是一种释负，就是不要固化思维：自然系统中是什么数值，那我一定要规定这个数值的大小。
总之，本次实验让我感受到了代码所构建的一个小小物理世界，也见到了代码绘制的有趣和多样化。果然，我还是很喜欢可视化的编程啊。

这篇关于代码本色学习之漂亮的球球在哪里的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---