本文主要是介绍AOE专题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一.AOE本质
每一个事件的发生表示以该事件相应的顶点为弧头所代表的活动都完成,以该事件相应的顶点的弧尾的弧所代表的活动可以开始。
二.AOE举例
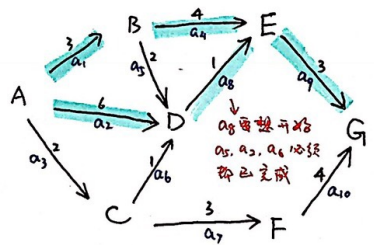
Ve:从始点开始到各顶点的最大(与本质联系)路径长度。
(从前往后,取最大值,Ve[0]=0即起始值为0)
Ve[j]=Max{Ve[i]+dis<i,j>}
Vl:在不推迟整个工期前提下,事件允许的最晚时间(从后往前,取小值,Vl[n]=Ve[n])
Vl[i]=Min{Vl-dis<i,j>}
A B C D E F G
Ve 0 3 2 6 7 5 10
Vl 0 3 3 6 7 6 10
e:活动ai最早开始时间,边活动的最早开始时间=它的发出顶点的最早发生时间(e(i)=Ve(k))
l:活动最晚开始时间,为边的到达顶点的最晚发生时间 - 边的权值
(L(i)=Vl(j)-dis<Vk,Vj>)
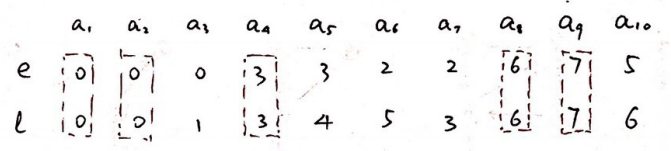
e[k]=l[k]即为关键活动
关键路径为(a1,a4,a9)和(a2,a8,a9)
PS:
(1)只有减少所有关键路径上共有的关键活动的时间才可能缩短工期
(2)只有在不改变最关键路径的前提下减少关键活动的时间才能缩短工期(如下题真题)
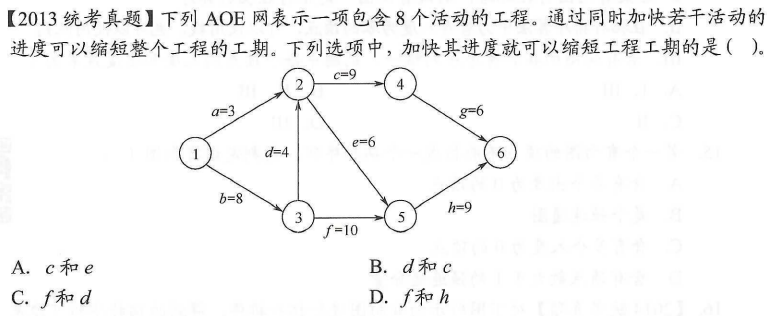
此处的AOE有3条关键路径:bdcg、bdeh和bfh。只有关键路径上的活动同时减少时,才能缩短工期。
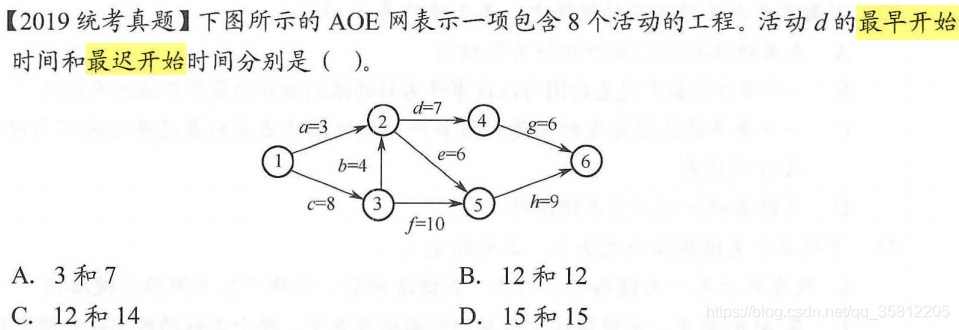
【解析】活动d的最早开始时间=该活动弧的起点所表示的事件(事件2)的最早发生时间=max{a,b+c}=max{3,12}=12。
活动d的最迟开始时间=该活动弧的终点所表示的事件的最迟发生时间 - 该活动用时。
图中关键路径=27=c+b+e+h(简单选择题就求出所有路径长度取max),
时间4的最迟发生时间=min{27-g}=min{27-6}=21,
活动d的最迟开始时间=21-d=21-7=14.
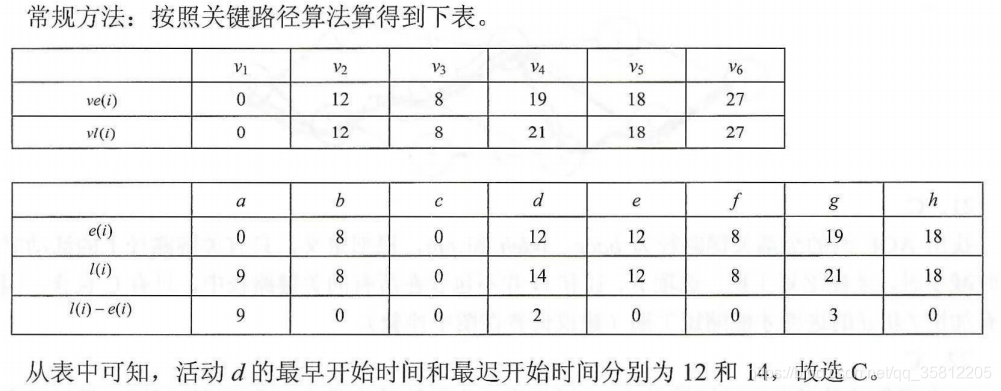
求关键路径例题
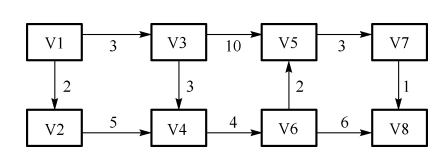
先求事件(点)的最早发生和最迟发生,再计算所有活动的最早和最迟发生时间。
| i | V1 | V2 | V3 | V4 | V5 | V6 | V7 | V8 |
| 最早发生时间 | 0 | 2 | 3 | 7 | 13 | 11 | 16 | 17 |
| 最晚发生时间 | 0 | 2 | 3 | 7 | 13 | 11 | 16 | 17 |
最晚发生时间:首先直接将V8的最早发生时间17写进V8的最晚发生时间,然后看V7(17-1=16);接着看V6,而因为V6的出度有两处(V5和V8),而V5还没算,所以可以先康V5的(由于V5的出边为3,所以V5的最晚发生时间为16-3=13),再回来康V6(一条去往V5求得11,一条去往V8也求得11,取min所以V6最晚发生时间为11)。
后两条:活动V3->V5最早发生时间是V3时间的最早开始时间,活动V3->V5的最晚开始时间是V5的最晚发生时间-前路径长度。

如V2-V4的最晚开始时间=V4的最晚发生时间 - dis【V2,V4】
最后,时间余量(活动的最早开始时间=最晚开始时间)为0的活动即关键路径,即把V3-V4边删去后的三条路径都是关键路径。
求V1结点到各点的最短路径和距离:

注意:虽然(3)中删去的是V3-V4的边(只是指关键路径V1到V8中),(4)的V1到其他顶点的最短路径是可以包括V3-V4边的。
老实人的算法流程




事件k的最迟发生时间:在不推迟整个工程完成的前提下,该事件最迟必须发生的时间。
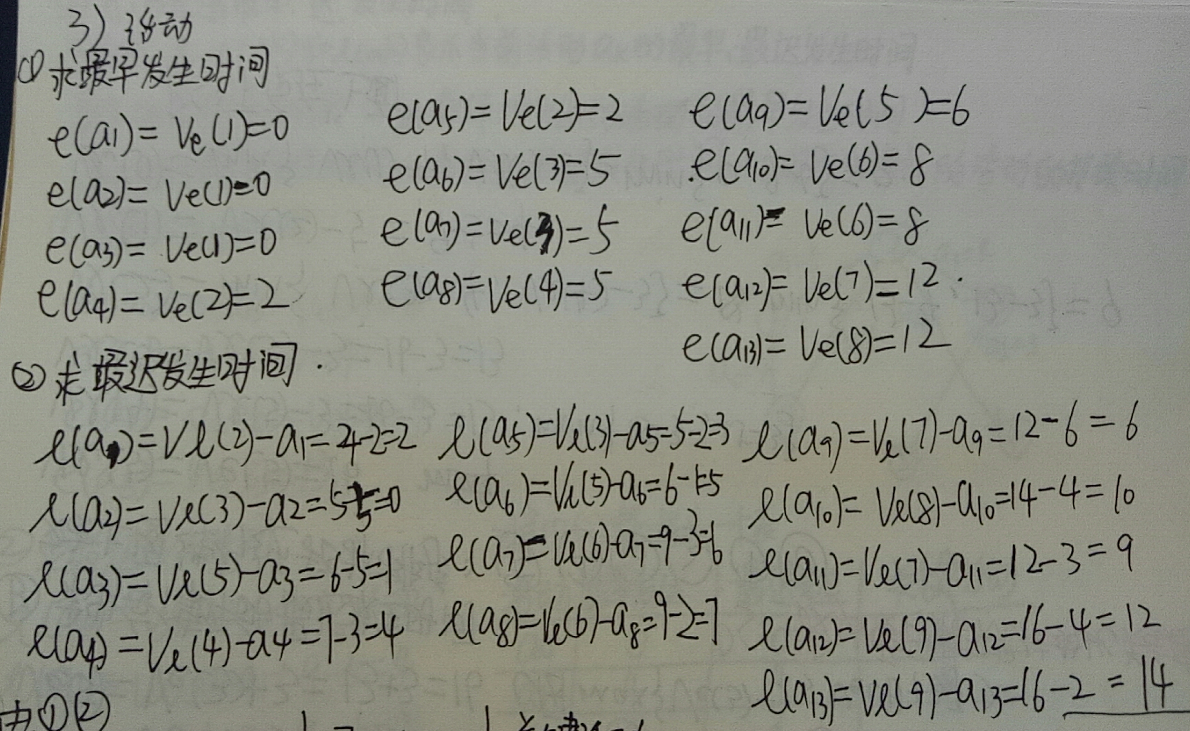
事件的最早发生时间:由这个事件所发出的活动的最早发生时间。

活动的最迟发生时间:事件的最迟发生时间减去以它为结束点的活动的持续时间。
这篇关于AOE专题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









