07.AOE网和图的关键路径

2023-12-30 01:50
文章标签 路径 关键 07 aoe 网和图

本文主要是介绍07.AOE网和图的关键路径，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

相关代码地址：https://gitee.com/gudongkun/datestruct

一、什么是AOE网

AOE(Activity on edge network) :在一个表示工程的带权有向图中，用顶点表示事件，用有向边表示活动，边上的权值表示活动的持续时间，称这样的有向图叫做边表示活动的网，简称AOE网

AOE网中没有入边的顶点称为始点（或源点）；没有出边的点称为终点（或汇点）

二、AOE网的性质

  1. 只有再某顶点所代表的事件发生后，从该顶点出发的活动才能开始；
  2. 只有再进入某顶点的各活动都结束，该顶点所代表的事件才能发生。

三、AOE网可以解决下列问题

  1. 完成整个工程至少需要多少时间
  2. 为缩短完成工程所需要的时间，应当加快哪些活动

四、关键活动

1.关键路径

从开始到结束最长的一条路径，可能不只一条，那么如何找到这样条路径呢？这就需要，找本节的重要概念关键活动 （全部由关键活动组成的路径，就是关键路径）

2.关键活动

（1）如果缩短某一条活动的时间，不能改变总体结束时间，活动就不是关键活动。
（2）如果缩短某条活动的时间，能减少总体结束时间,活动就是关键活动。
（3）活动的最早发生时间，和最迟发生时间一样，活动，就是关键活动。

五、求关键活动

上文说到，活动的最早发生时间，和最迟发生时间一样，活动，就是关键活动。
这两个时间怎么求呢？下面将给出答案。

1.关键活动的4个前导量

（1）事件A的最早发生时间event_early[B] ：event_early[B] = max{event_early[BeforeB]+len<BeforeB,B>}
（2）事件A的最迟发生时间event_latest[B]：event_latest[B] = min{event_latest[AfterB]-len<B,AfterB>}
（3）活动AB 的最早发生时间 activity_early ：activity_early[BC] = event_early[B]
（4）活动AB 的最迟发生时间 activity_latest : activity_latest[CD] = event_latest[D] - len[CD]

注：len<A,B>表示 弧AB的长度

img

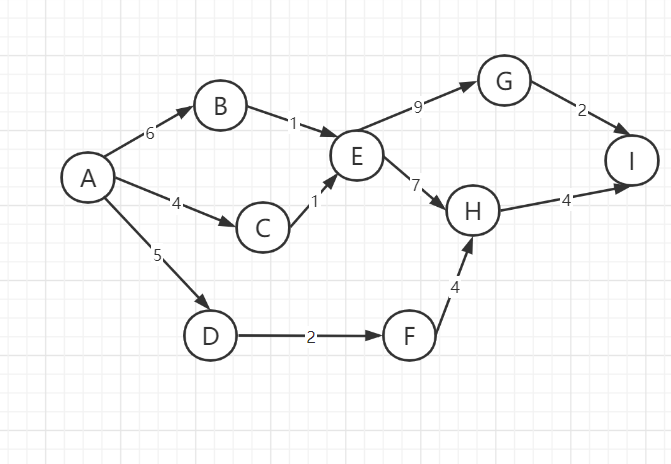
(1) event_early分析

event ： A B C D E F G H I
event_early ： 0 6 4 5 7 7 16 14 18

  1. 从起点开始算，起点时间一定是0
  2. 之后的事件用前一个事件的时间推算如：
    1. event_early[B] = max{event_early[A]+len<A,B>}
    2. event_early[E] = max{event_early[B]+len<B,E> ，event_early[C]+len<C,E>}
（2）event_latest分析,依赖event_early

event ： A B C D E F G H I
event_early ： 0 6 4 5 7 7 16 14 18
event_latest： 0 6 6 8 7 10 16 14 18

  1. 从后往前计算，结束事件直接取event_early
  2. 用前一个事件的时间推算如：event_latest[B] = min{event_latest[C]-len<A,B>}
  3. 开始时间，必定是0
（3）activity_early 分析

活动BC 的最早开始时间应该等于 时间B的最早开始时间因此有：activity_early[BC] = event_early[B]

 event       ： A B  C D  E  F  G  H  Ievent_early ： 0 6  4 5  7  7  16 14 18event_latest： 0 6  6  8 7 10 16 14 18activity       : AB  AC   AD    BE  CE  DF  EG  EH  FH  GI  HI            activity_early : 0    0    0    6   4   5   7   7   7   16  14
(4) activity_latest分析

img

activity_latest 要从前往后算

例如活动CD 的最晚开始时间要保证时间D的最迟时间不能拖后所有：activity_latest[CD] = event_latest[D] - len[CD]

 event       ： A B C D E  F  G  H  Ievent_early ： 0 6  4 5  7  7  16 14 18event_latest： 0 6  6  8 7 10 16 14 18activity       : AB  AC   AD   BE   CE  DF  EG  EH  FH  GI  HI            activity_early : 0    0    0    6   4   5   7   7   7   16  14activity_latest: 0    2    3    6   6   8   7   11  10  16  14
2.关键活动：

最早开始时间和最晚开始时间是一样的称为关键活动。

 activity      : (AB)  AC  AD  (BE)  CE  DF (EG) (EH)  FH  (GI)  (HI)            activity_early : 0    0    0    6   4   5   7    7    7    16    14activity_latest: 0    2    3    6   6   8   7    7    10   16    14

img

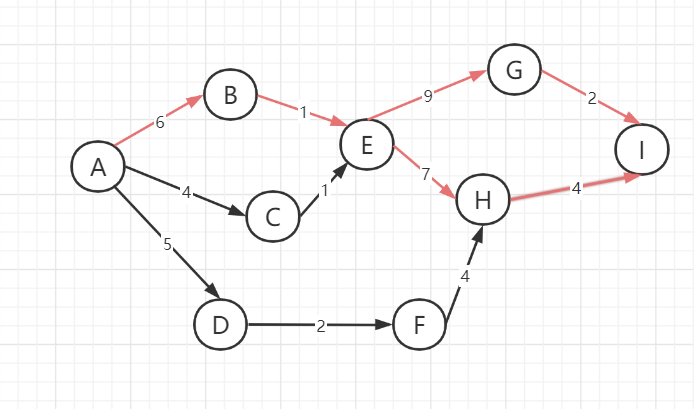
注意：

  1. 关键活动组成的路径叫关键路径
  2. 虽然会产生多条关键路径，但是多条关键路径的执行时间是一样的。
  3. 工程的总执行时间就是任意选其中一条关键路径的总执行时间。

六、动画演示

https://www.bilibili.com/video/BV1PW41187vc

七、代码实现

aoe.go

package aoeimport ("fmt""gitee.com/gudongkun/datestruct/dataStructures/graph""gitee.com/gudongkun/datestruct/dataStructures/linear"
)func GetGraph() graph.DMGraph {g := graph.NewDMGraph()g.AddNode("A")g.AddNode("B")g.AddNode("C")g.AddNode("D")g.AddNode("E")g.AddNode("F")g.AddNode("G")g.AddNode("H")g.AddNode("I")g.AddEdge("A", "B", 6)g.AddEdge("A", "C", 4)g.AddEdge("A", "D", 5)g.AddEdge("B", "E", 1)g.AddEdge("C", "E", 1)g.AddEdge("E", "G", 9)g.AddEdge("E", "H", 7)g.AddEdge("G", "I", 2)g.AddEdge("H", "I", 4)g.AddEdge("D", "F", 2)g.AddEdge("F", "H", 4)return g
}func AOEKeyEvents() []string {g := GetGraph()eventEarly := make(map[string]int)eventLatest := make(map[string]int)activeEarly := make(map[string]int)activeLatest := make(map[string]int)// 1. 求eventEarlyindegrees := make(map[string]int)stack := linear.NewStack()for _, v := range g.Nodes {indegrees[v] = g.GetIndegree(v)if indegrees[v] == 0 {stack.Push(v)indegrees[v] = -1eventEarly[v] = 0}}for !stack.IsEmpty() {v, _ := stack.Pop()for _, edge := range g.GetEdgesByHead(v) {indegrees[edge.Tail]--if indegrees[edge.Tail] == 0 {stack.Push(edge.Tail)indegrees[edge.Tail] = -1for _, endEdge := range g.GetEdgesByTail(edge.Tail) {val, ok := eventEarly[edge.Tail]if !ok {eventEarly[edge.Tail] = eventEarly[endEdge.Head] + endEdge.Val} else {if val < eventEarly[endEdge.Head]+endEdge.Val {eventEarly[edge.Tail] = val}}}}}}// 2. 求eventLatestoutdegrees := make(map[string]int)outstack := linear.NewStack()for _, v := range g.Nodes {outdegrees[v] = g.GetOutdegree(v)if outdegrees[v] == 0 {outstack.Push(v)outdegrees[v] = -1eventLatest[v] = eventEarly[v]}}for !outstack.IsEmpty() {v, _ := outstack.Pop()for _, edge := range g.GetEdgesByTail(v) {outdegrees[edge.Head]--if outdegrees[edge.Head] == 0 {outstack.Push(edge.Head)outdegrees[edge.Head] = -1for _, endEdge := range g.GetEdgesByHead(edge.Head) {val, ok := eventLatest[edge.Head]if !ok {eventLatest[edge.Head] = eventLatest[endEdge.Tail] - endEdge.Val} else {if val < eventLatest[endEdge.Tail]-endEdge.Val {eventLatest[edge.Head] = val}}}}}}// 3.求 activityEarlyfor _, v := range g.GetEdgeList() {activeEarly[v.Head+"-"+v.Tail] = eventEarly[v.Head]}// 4. 求activeLatestfor _, v := range g.GetEdgeList() {activeLatest[v.Head+"-"+v.Tail] = eventLatest[v.Tail] - v.Val}// 5.关键活动var keyActivity []stringfor k,v := range activeEarly {if activeLatest[k] == v {keyActivity = append(keyActivity,k)}}fmt.Println(keyActivity)return keyActivity}

aoe_test.go

package aoeimport "testing"func TestAOEKeyEvents(t *testing.T) {list := AOEKeyEvents()if len(list) != 6 {t.Fail()}
}

添加了新方法的 有向图 dmgraph.go

package graphimport ("errors"
)const DMaxSize = 20
const DMaxNum = 99999type DMGraph struct {Edges   [DMaxSize][DMaxSize]intEdgeNum intNodes   []stringIndexs  map[string]int
}type DEdge struct {Head, Tail stringVal        int
}func NewDMGraph() DMGraph {var g DMGraphfor k, v := range g.Edges {for kk, _ := range v {if k == kk {g.Edges[k][kk] = 0} else {g.Edges[k][kk] = DMaxNum}}}g.Indexs = make(map[string]int)return g}func (g *DMGraph) AddNode(nodeName string) error {if g.Indexs == nil {return errors.New("不是有效的图")}if _, ok := g.Indexs[nodeName]; ok {return errors.New("已经添加过此结点")}g.Indexs[nodeName] = len(g.Nodes)g.Nodes = append(g.Nodes, nodeName)return nil
}func (g *DMGraph) AddEdge(Head, Tail string, val int) error {if _, ok := g.Indexs[Head]; !ok {return errors.New("结点不存在：" + Head)}if _, ok := g.Indexs[Tail]; !ok {return errors.New("结点不存在：" + Tail)}if g.Edges[g.Indexs[Head]][g.Indexs[Tail]] != DMaxNum {return errors.New("边已经存在")}g.Edges[g.Indexs[Head]][g.Indexs[Tail]] = valg.EdgeNum++return nil
}func (g *DMGraph) GetEdgeList() []DEdge {var edgeList []DEdgefor i := 0; i < len(g.Nodes); i++ {for j := 0; j < len(g.Nodes); j++ {if g.Edges[i][j] != DMaxNum && i != j {edgeList = append(edgeList,DEdge{Head: g.Nodes[i], Tail: g.Nodes[j], Val: g.Edges[i][j]},)}}}return edgeList
}func (g *DMGraph) GetIndegree(ele string) int {tail, ok := g.Indexs[ele]if !ok {return -1 //点不存在}indegree := 0for i := 0; i < len(g.Nodes); i++ {if g.Edges[i][tail] != 0 && g.Edges[i][tail] != DMaxNum {indegree++}}return indegree
}func (g *DMGraph) GetOutdegree(ele string) int {head, ok := g.Indexs[ele]if !ok {return -1 //点不存在}outdegree := 0for i := 0; i < len(g.Nodes); i++ {if g.Edges[head][i] != 0 && g.Edges[head][i] != DMaxNum {outdegree++}}return outdegree}func (g *DMGraph) GetEdgesByTail(ele string) []DEdge {var edgeList []DEdgetail, ok := g.Indexs[ele]if !ok {return nil}for i := 0; i < len(g.Nodes); i++ {if g.Edges[i][tail] != 0 && g.Edges[i][tail] != DMaxNum {edgeList = append(edgeList,DEdge{Head: g.Nodes[i], Tail: g.Nodes[tail], Val: g.Edges[i][tail]},)}}return edgeList
}func (g *DMGraph) GetEdgesByHead(ele string) []DEdge {var edgeList []DEdgehead, ok := g.Indexs[ele]if !ok {return nil}for i := 0; i < len(g.Nodes); i++ {if g.Edges[head][i] != 0 && g.Edges[head][i] != DMaxNum {edgeList = append(edgeList,DEdge{Head: g.Nodes[head], Tail: g.Nodes[i], Val: g.Edges[head][i]},)}}return edgeList
}

这篇关于07.AOE网和图的关键路径的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/551340。

相关文章

Linux修改pip和conda缓存路径的几种方法

Linux修改pip和conda缓存路径的几种方法

《Linux修改pip和conda缓存路径的几种方法》在Python生态中,pip和conda是两种常见的软件包管理工具,它们在安装、更新和卸载软件包时都会使用缓存来提高效率,适当地修改它们的缓存路径... 目录一、pip 和 conda 的缓存机制1. pip 的缓存机制默认缓存路径2. conda 的缓
阅读更多...
Windows系统下如何查找JDK的安装路径

Windows系统下如何查找JDK的安装路径

《Windows系统下如何查找JDK的安装路径》：本文主要介绍Windows系统下如何查找JDK的安装路径,文中介绍了三种方法,分别是通过命令行检查、使用verbose选项查找jre目录、以及查看... 目录一、确认是否安装了JDK二、查找路径三、另外一种方式如果很久之前安装了JDK，或者在别人的电脑上，想
阅读更多...
Python中Windows和macOS文件路径格式不一致的解决方法

Python中Windows和macOS文件路径格式不一致的解决方法

《Python中Windows和macOS文件路径格式不一致的解决方法》在Python中,Windows和macOS的文件路径字符串格式不一致主要体现在路径分隔符上,这种差异可能导致跨平台代码在处理文... 目录方法 1：使用 os.path 模块方法 2：使用 pathlib 模块（推荐）方法 3：统一使
阅读更多...
一文教你解决Python不支持中文路径的问题

一文教你解决Python不支持中文路径的问题

《一文教你解决Python不支持中文路径的问题》Python是一种广泛使用的高级编程语言,然而在处理包含中文字符的文件路径时,Python有时会表现出一些不友好的行为,下面小编就来为大家介绍一下具体的... 目录问题背景解决方案1. 设置正确的文件编码2. 使用pathlib模块3. 转换路径为Unicod
阅读更多...
MySQL9.0默认路径安装下重置root密码

MySQL9.0默认路径安装下重置root密码

《MySQL9.0默认路径安装下重置root密码》本文主要介绍了MySQL9.0默认路径安装下重置root密码,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们... 目录问题描述环境描述解决方法正常模式下修改密码报错原因问题描述mysqlChina编程采用默认安装路径，
阅读更多...
python获取当前文件和目录路径的方法详解

python获取当前文件和目录路径的方法详解

《python获取当前文件和目录路径的方法详解》：本文主要介绍Python中获取当前文件路径和目录的方法,包括使用__file__关键字、os.path.abspath、os.path.realp... 目录1、获取当前文件路径2、获取当前文件所在目录3、os.path.abspath和os.path.re
阅读更多...
hdu2544（单源最短路径）

hdu2544（单源最短路径）

模板题： //题意：求1到n的最短路径，模板题#include<iostream>#include<algorithm>#include<cstring>#include<stack>#include<queue>#include<set>#include<map>#include<stdio.h>#include<stdlib.h>#include<ctype.h>#i
阅读更多...
poj 1734 （floyd求最小环并打印路径）

poj 1734 （floyd求最小环并打印路径）

题意： 求图中的一个最小环，并打印路径。 解析： ans 保存最小环长度。 一直wa，最后终于找到原因，inf开太大爆掉了。。。 虽然0x3f3f3f3f用memset好用，但是还是有局限性。 代码： #include <iostream>#include <cstdio>#include <cstdlib>#include <algorithm>#incl
阅读更多...
【408DS算法题】039进阶-判断图中路径是否存在

【408DS算法题】039进阶-判断图中路径是否存在

Index 题目分析实现总结 题目 对于给定的图G，设计函数实现判断G中是否含有从start结点到stop结点的路径。 分析实现 对于图的路径的存在性判断，有两种做法：（本文的实现均基于邻接矩阵存储方式的图） 1.图的BFS BFS的思路相对比较直观——从起始结点出发进行层次遍历，遍历过程中遇到结点i就表示存在路径start->i，故只需判断每个结点i是否就是stop
阅读更多...
Android Environment 获取的路径问题

Android Environment 获取的路径问题

1. 以获取 /System 路径为例 /*** Return root of the "system" partition holding the core Android OS.* Always present and mounted read-only.*/public static @NonNull File getRootDirectory() {return DIR_ANDR
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2