本文主要是介绍电信保温杯笔记——《统计学习方法(第二版)——李航》第8章 提升方法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
电信保温杯笔记——《统计学习方法(第二版)——李航》第8章 提升方法
- 论文
- 介绍
- 提升方法的基本思路
- 提升方法的代表:AdaBoost
- 步骤
- 例子
- 误差分析
- AdaBoost的另一个解释
- 前向分步算法
- 前向分步算法与AdaBoost的关系
- 提升方法的实例:提升树(boosting tree)
- 提升树模型
- 提升树算法
- 步骤
- 例子
- 提升树的优化
- 步骤
- 本章概要
- 相关视频
- 相关的笔记
- 相关代码
- pytorch
- tensorflow
- keras
- pytorch API:
- tensorflow API
论文
Boosting算法:《A Short Introduction to Boosting》
AdaBoost算法:《A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting》
提升树算法:《Additive logistic regression: a statistical view of boosting (with discussion and a rejoinder by the authors)》
介绍
电信保温杯笔记——《统计学习方法(第二版)——李航》
本文是对原书的精读,会有大量原书的截图,同时对书上不详尽的地方进行细致解读与改写。
提升(boosting)方法是一种常用的统计学习方法,应用广泛且有效。在分类问题中,它通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,提高分类的性能。

下文首先介绍提升方法的思路和代表性的提升算法 AdaBoost;然后分析AdaBoost的误差;并且从另一个角度解释AdaBoost算法;最后叙述提升方法更具体的实例——提升树(boosting tree)。
提升方法的基本思路

为了方便理解下文,这里需要介绍一下对于线性分类器来说,数据集线性可分和线性不可分这2个概念。

定义2.2:

对于线性分类器来说,分类准确率接近90%应该算的上是接近线性可分的,准确率70+%的应该算的上是完全线性不可分的,笼统地理解为线性不可分就行。
概率近似正确(probably approximately correct,PAC)这个概念,在使用线性分类器分类任务中,应该说的是接近线性可分的,分类准确率接近90%,也可简单地理解为“强可学习”,而“弱可学习”可简单地理解为线性不可分,准确率70+%。
有了这些概念再去看原文:


提升方法的代表:AdaBoost
关于第1个问题,AdaBoost的做法是,提高那些被前一轮弱分类器错误分类样本的权值,而降低那些被正确分类样本的权值。这样一来,那些没有得到正确分类的数据,由于其权值的加大而受到后一轮的弱分类器的更大关注。于是,分类问题被一系列的弱分类器“分而治之”。至于第2个问题,即弱分类器的组合,AdaBoost采取加权多数表决的方法。具体地,加大分类误差率小的弱分类器的权值,使其在表决中起较大的作用,减小分类误差率大的弱分类器的权值,使其在表决中起较小的作用。
AdaBoost的巧妙之处就在于它将这些想法自然且有效地实现在一种算法里。



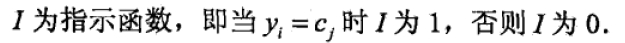
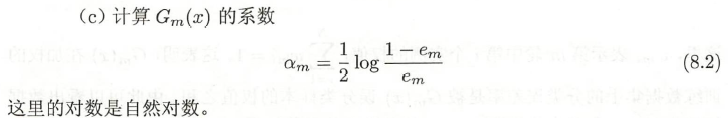
式子(8.2)有点像电信保温杯笔记——《统计学习方法(第二版)——李航》第6章 逻辑斯谛回归与最大熵模型的逻辑斯谛回归模型中的对数几率:

分类误差越小,系数 α m \alpha_m αm 越大。

令 Z m , i = w m i e x p ( − α m y i G m ( x i ) ) Z_m,i = w_{mi} exp(-\alpha_m y_i G_m(x_i)) Zm,i=wmiexp(−αmyiGm(xi)),则式子(8.4)和(8.5)变成
w m + 1 , i = Z m , i Z m Z m = ∑ i = 1 N Z m , i w_{m+1,i} = \frac{Z_{m,i}}{Z_m} \\ Z_m = \sum\limits_{i = 1}^N Z_{m,i} wm+1,i=ZmZm,iZm=i=1∑NZm,i
可以认为分子 Z m , i Z_{m,i} Zm,i 是样本的新权重的得分分值,分母 Z m Z_m Zm 是归一化因子。
对于第 m m m 个 分类器来说,第 i i i 个样本分类正确, y i G m ( x i ) y_i G_m(x_i) yiGm(xi) 为1, 0 < e x p ( − α m y i G m ( x i ) ) < 1 0<exp(-\alpha_m y_i G_m(x_i))<1 0<exp(−αmyiGm(xi))<1,分值 Z m , i Z_{m,i} Zm,i 下降,在训练集的第 m + 1 m+1 m+1 个分布上的权重 w m + 1 , i w_{m+1,i} wm+1,i 减小;
如果分类错误, y i G m ( x i ) y_i G_m(x_i) yiGm(xi) 为 − 1 -1 −1, e x p ( − α m y i G m ( x i ) ) > 1 exp(-\alpha_m y_i G_m(x_i))>1 exp(−αmyiGm(xi))>1,分值 Z m , i Z_{m,i} Zm,i 上升,在训练集的第 m + 1 m+1 m+1 个分布上的权重 w m + 1 , i w_{m+1,i} wm+1,i 增大。

步骤


例子



误差分析

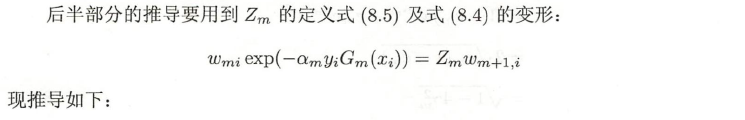
1 N ∑ i = 1 N exp ( − y i f ( x i ) ) = 1 N ∑ i = 1 N exp ( − ∑ m = 1 M α m y i G m ( x i ) ) = ∑ i = 1 N 1 N exp ( − ∑ m = 1 M α m y i G m ( x i ) ) = ∑ i = 1 N w 1 i exp ( − ∑ m = 1 M α m y i G m ( x i ) ) = ∑ i = 1 N w 1 i ∏ m = 1 M exp ( − α m y i G m ( x i ) ) = ∑ i = 1 N w 1 i exp ( − α 1 y i G 1 ( x i ) ) ∏ m = 2 M exp ( − α m y i G m ( x i ) ) = ∑ i = 1 N Z 1 w 2 i ∏ m = 2 M exp ( − α m y i G m ( x i ) ) = Z 1 ∑ i = 1 N w 2 i ∏ m = 2 M exp ( − α m y i G m ( x i ) ) = Z 1 Z 2 ∑ i = 1 N w 3 i ∏ m = 3 M exp ( − α m y i G m ( x i ) ) = ⋯ = Z 1 Z 2 ⋯ Z M − 1 ∑ i = 1 N w M i exp ( − α M y i G M ( x i ) ) = ∏ m = 1 M Z m \begin{aligned} \frac{1}{N} \sum\limits_{i=1}^N \exp (-y_if(x_i)) &= \frac{1}{N} \sum\limits_{i=1}^N \exp \left(- \sum\limits_{m=1}^M \alpha_m y_i G_m(x_i) \right) \\ &= \sum\limits_{i=1}^N \frac{1}{N} \exp \left(- \sum\limits_{m=1}^M \alpha_m y_i G_m(x_i) \right) \\ &= \sum\limits_{i=1}^N w_{1i} \exp \left(- \sum\limits_{m=1}^M \alpha_m y_i G_m(x_i) \right) \\ &= \sum\limits_{i=1}^N w_{1i} \prod\limits_{m = 1}^M \exp (- \alpha_m y_i G_m(x_i) ) \\ &= \sum\limits_{i=1}^N w_{1i} \exp (- \alpha_1 y_i G_1(x_i) ) \prod\limits_{m = 2}^M \exp (- \alpha_m y_i G_m(x_i) ) \\ &= \sum\limits_{i=1}^N Z_1 w_{2i} \prod\limits_{m = 2}^M \exp (- \alpha_m y_i G_m(x_i) ) \\ &= Z_1 \sum\limits_{i=1}^N w_{2i} \prod\limits_{m = 2}^M \exp (- \alpha_m y_i G_m(x_i) ) \\ &= Z_1Z_2 \sum\limits_{i=1}^N w_{3i} \prod\limits_{m = 3}^M \exp (- \alpha_m y_i G_m(x_i) ) \\ &= \cdots \\ &= Z_1 Z_2 \cdots Z_{M-1} \sum\limits_{i=1}^N w_{Mi} \exp (- \alpha_M y_i G_M(x_i) ) \\ &= \prod\limits_{m = 1}^M Z_m \end{aligned} N1i=1∑Nexp(−yif(xi))=N1i=1∑Nexp(−m=1∑MαmyiGm(xi))=i=1∑NN1exp(−m=1∑MαmyiGm(xi))=i=1∑Nw1iexp(−m=1∑MαmyiGm(xi))=i=1∑Nw1im=1∏Mexp(−αmyiGm(xi))=i=1∑Nw1iexp(−α1yiG1(xi))m=2∏Mexp(−αmyiGm(xi))=i=1∑NZ1w2im=2∏Mexp(−αmyiGm(xi))=Z1i=1∑Nw2im=2∏Mexp(−αmyiGm(xi))=Z1Z2i=1∑Nw3im=3∏Mexp(−αmyiGm(xi))=⋯=Z1Z2⋯ZM−1i=1∑NwMiexp(−αMyiGM(xi))=m=1∏MZm

Z m = ∑ i = 1 N w m i exp ( − α m y i G m ( x i ) ) = ∑ y i = G m ( x i ) w m i e − α m + ∑ y i ≠ G m ( x i ) w m i e α m = e − α m ∑ y i = G m ( x i ) w m i + e α m ∑ y i ≠ G m ( x i ) w m i = e − α m ( 1 − e m ) + e α m e m ≥ 2 ( 1 − e m ) e m ( 8.11 ) \begin{aligned} Z_m & = \sum\limits_{i=1}^N w_{mi} \exp (- \alpha_m y_i G_m(x_i) ) \\ &= \sum\limits_{y_i = G_m(x_i)} w_{mi} e^{- \alpha_m} + \sum\limits_{y_i \neq G_m(x_i)} w_{mi} e^{\alpha_m} \\ &= e ^{- \alpha_m} \sum\limits_{y_i = G_m(x_i)} w_{mi} + e ^{\alpha_m}\sum\limits_{y_i \neq G_m(x_i)} w_{mi} \\ &= e ^{- \alpha_m} (1 - e_m) + e^{\alpha_m} e_m \\ & \ge2\sqrt{(1-e_m)e_m} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(8.11) \end{aligned} Zm=i=1∑Nwmiexp(−αmyiGm(xi))=yi=Gm(xi)∑wmie−αm+yi=Gm(xi)∑wmieαm=e−αmyi=Gm(xi)∑wmi+eαmyi=Gm(xi)∑wmi=e−αm(1−em)+eαmem≥2(1−em)em(8.11)
当且仅当 e − α m ( 1 − e m ) = e α m e m e ^{- \alpha_m} (1 - e_m) = e^{\alpha_m} e_m e−αm(1−em)=eαmem 时,
e − α m ( 1 − e m ) + e α m e m = 2 ( 1 − e m ) e m e ^{- \alpha_m} (1 - e_m) + e^{\alpha_m} e_m = 2\sqrt{(1-e_m)e_m} e−αm(1−em)+eαmem=2(1−em)em 成立。
根据公式(8.2)
α m = 1 2 log 1 − e m e m 2 α m = log 1 − e m e m e 2 α m = 1 − e m e m e α m e m = e − α m ( 1 − e m ) \begin{aligned} \alpha_m & = \frac{1}{2} \log \frac{1-e_m}{e_m} \\ 2 \alpha_m & = \log \frac{1-e_m}{e_m} \\ e^{2 \alpha_m} &= \frac{1-e_m}{e_m} \\ e^{ \alpha_m} e_m &= e^{- \alpha_m} (1-e_m) \\ \end{aligned} αm2αme2αmeαmem=21logem1−em=logem1−em=em1−em=e−αm(1−em)
因此
Z m = 2 ( 1 − e m ) e m = 1 − 4 γ m 2 ( 8.11 ) \begin{aligned} Z_m &= 2\sqrt{(1-e_m)e_m} \\ &= \sqrt{1-4\gamma_m^2} \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad(8.11) \end{aligned} Zm=2(1−em)em=1−4γm2(8.11)

AdaBoost的另一个解释
这一部分不看也没关系。

前向分步算法


前向分步算法与AdaBoost的关系


∑ i = 1 N w ˉ m i exp [ − y i α G ( x i ) ] = ∑ y i = G m ( x i ) N w ˉ m i e − α + ∑ y i ≠ G m ( x i ) N w ˉ m i e α = ∑ y i = G m ( x i ) N w ˉ m i e − α + ( ∑ y i ≠ G m ( x i ) N w ˉ m i e − α − ∑ y i ≠ G m ( x i ) N w ˉ m i e − α ) + ∑ y i ≠ G m ( x i ) N w ˉ m i e α = ( ∑ y i = G m ( x i ) N w ˉ m i e − α + ∑ y i ≠ G m ( x i ) N w ˉ m i e − α ) − ∑ y i ≠ G m ( x i ) N w ˉ m i e − α + ∑ y i ≠ G m ( x i ) N w ˉ m i e α = ∑ i = 1 N w ˉ m i e − α + ∑ y i ≠ G m ( x i ) N w ˉ m i ( e α − e − α ) = ∑ i = 1 N w ˉ m i e − α + ∑ i = 1 N w ˉ m i ( e α − e − α ) I ( y i ≠ G ( x i ) ) ( 8.22 ) \begin{aligned} \sum\limits_{i=1}^N \bar{w}_{mi} \exp [-y_i \alpha G(x_i)] & = \sum\limits_{y_i=G_m(x_i)}^N \bar{w}_{mi} e^{-\alpha} + \sum\limits_{y_i \neq G_m(x_i)}^N \bar{w}_{mi} e^{\alpha} \\ & = \sum\limits_{y_i=G_m(x_i)}^N \bar{w}_{mi} e^{-\alpha} + ( \sum\limits_{y_i \neq G_m(x_i)}^N \bar{w}_{mi} e^{-\alpha} - \sum\limits_{y_i \neq G_m(x_i)}^N \bar{w}_{mi} e^{-\alpha} )+ \sum\limits_{y_i \neq G_m(x_i)}^N \bar{w}_{mi} e^{\alpha} \\ & = ( \sum\limits_{y_i=G_m(x_i)}^N \bar{w}_{mi} e^{-\alpha} + \sum\limits_{y_i \neq G_m(x_i)}^N \bar{w}_{mi} e^{-\alpha} ) - \sum\limits_{y_i \neq G_m(x_i)}^N \bar{w}_{mi} e^{-\alpha} + \sum\limits_{y_i \neq G_m(x_i)}^N \bar{w}_{mi} e^{\alpha} \\ & = \sum\limits_{i=1}^N \bar{w}_{mi} e^{-\alpha} + \sum\limits_{y_i \neq G_m(x_i)}^N \bar{w}_{mi} (e^{\alpha} - e^{-\alpha}) \\ & = \sum\limits_{i=1}^N \bar{w}_{mi} e^{-\alpha} + \sum\limits_{i = 1}^N \bar{w}_{mi} (e^{\alpha} - e^{-\alpha}) I(y_i \neq G(x_i)) \quad\quad\quad\quad\quad\quad\quad\quad(8.22) \end{aligned} i=1∑Nwˉmiexp[−yiαG(xi)]=yi=Gm(xi)∑Nwˉmie−α+yi=Gm(xi)∑Nwˉmieα=yi=Gm(xi)∑Nwˉmie−α+(yi=Gm(xi)∑Nwˉmie−α−yi=Gm(xi)∑Nwˉmie−α)+yi=Gm(xi)∑Nwˉmieα=(yi=Gm(xi)∑Nwˉmie−α+yi=Gm(xi)∑Nwˉmie−α)−yi=Gm(xi)∑Nwˉmie−α+yi=Gm(xi)∑Nwˉmieα=i=1∑Nwˉmie−α+yi=Gm(xi)∑Nwˉmi(eα−e−α)=i=1∑Nwˉmie−α+i=1∑Nwˉmi(eα−e−α)I(yi=G(xi))(8.22)
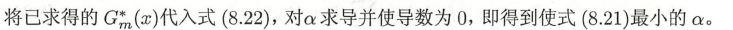
∂ ( ∑ i = 1 N w ˉ m i exp [ − y i α G ( x i ) ] ) ∂ α = ∂ ( ∑ i = 1 N w ˉ m i e − α + ∑ i = 1 N w ˉ m i ( e α − e − α ) I ( y i ≠ G ( x i ) ) ) ∂ α = α e − α ( − ∑ i = 1 N w ˉ m i + ( e 2 α + 1 ) ∑ i = 1 N w ˉ m i I ( y i ≠ G ( x i ) ) ) = 0 \begin{aligned} \frac{ \partial \left( \sum\limits_{i=1}^N \bar{w}_{mi} \exp [-y_i \alpha G(x_i)] \right)}{ \partial \alpha} & = \frac{ \partial \left( \sum\limits_{i=1}^N \bar{w}_{mi} e^{-\alpha} + \sum\limits_{i = 1}^N \bar{w}_{mi} (e^{\alpha} - e^{-\alpha}) I(y_i \neq G(x_i)) \right)}{ \partial \alpha} \\ &= \alpha e^{-\alpha} \left( -\sum\limits_{i=1}^N \bar{w}_{mi} + (e^{2\alpha} + 1) \sum\limits_{i = 1}^N \bar{w}_{mi} I(y_i \neq G(x_i)) \right) \\ &= 0 \end{aligned} ∂α∂(i=1∑Nwˉmiexp[−yiαG(xi)])=∂α∂(i=1∑Nwˉmie−α+i=1∑Nwˉmi(eα−e−α)I(yi=G(xi)))=αe−α(−i=1∑Nwˉmi+(e2α+1)i=1∑NwˉmiI(yi=G(xi)))=0
于是
− ∑ i = 1 N w ˉ m i + ( e 2 α + 1 ) ∑ i = 1 N w ˉ m i I ( y i ≠ G ( x i ) ) = 0 e 2 α ∑ i = 1 N w ˉ m i I ( y i ≠ G ( x i ) ) = ∑ i = 1 N w ˉ m i − ∑ i = 1 N w ˉ m i I ( y i ≠ G ( x i ) ) e 2 α = ∑ i = 1 N w ˉ m i − ∑ i = 1 N w ˉ m i I ( y i ≠ G ( x i ) ) ∑ i = 1 N w ˉ m i I ( y i ≠ G ( x i ) ) α = 1 2 log ∑ i = 1 N w ˉ m i − ∑ i = 1 N w ˉ m i I ( y i ≠ G ( x i ) ) ∑ i = 1 N w ˉ m i I ( y i ≠ G ( x i ) ) α = 1 2 log 1 − e m e m \begin{aligned} & -\sum\limits_{i=1}^N \bar{w}_{mi} + (e^{2\alpha} + 1) \sum\limits_{i = 1}^N \bar{w}_{mi} I(y_i \neq G(x_i)) = 0 \\ & e^{2\alpha} \sum\limits_{i = 1}^N \bar{w}_{mi} I(y_i \neq G(x_i)) = \sum\limits_{i=1}^N \bar{w}_{mi} - \sum\limits_{i = 1}^N \bar{w}_{mi} I(y_i \neq G(x_i)) \\ & e^{2\alpha} = \frac{ \sum\limits_{i=1}^N \bar{w}_{mi} - \sum\limits_{i = 1}^N \bar{w}_{mi} I(y_i \neq G(x_i)) }{ \sum\limits_{i = 1}^N \bar{w}_{mi} I(y_i \neq G(x_i)) } \\ & \alpha = \frac{1}{2} \log \frac{ \sum\limits_{i=1}^N \bar{w}_{mi} - \sum\limits_{i = 1}^N \bar{w}_{mi} I(y_i \neq G(x_i)) }{ \sum\limits_{i = 1}^N \bar{w}_{mi} I(y_i \neq G(x_i)) } \\ & \alpha = \frac{1}{2} \log \frac{ 1 - e_m }{ e_m } \end{aligned} −i=1∑Nwˉmi+(e2α+1)i=1∑NwˉmiI(yi=G(xi))=0e2αi=1∑NwˉmiI(yi=G(xi))=i=1∑Nwˉmi−i=1∑NwˉmiI(yi=G(xi))e2α=i=1∑NwˉmiI(yi=G(xi))i=1∑Nwˉmi−i=1∑NwˉmiI(yi=G(xi))α=21logi=1∑NwˉmiI(yi=G(xi))i=1∑Nwˉmi−i=1∑NwˉmiI(yi=G(xi))α=21logem1−em

提升方法的实例:提升树(boosting tree)
提升树是以分类树或回归树为基本分类器的提升方法。提升树被认为是统计学习中性能最好的方法之一。
提升树模型

提升树算法


每一棵树都拟合前一棵树的残差,即对前一棵树预测的误差进行修补。下图每多一棵树,预测值就越来越接近真实值:

实线表示 f i ( x i ) f_i(x_i) fi(xi) 的预测值,虚线表示 f i ( x i ) f_i(x_i) fi(xi) 相较于 f i − 1 ( x i ) f_{i-1}(x_i) fi−1(xi) 变换的部分。
直接看例题比较好。
步骤

例子



提升树的优化


步骤

本章概要

相关视频
相关的笔记
hktxt /Learn-Statistical-Learning-Method
相关代码
Dod-o /Statistical-Learning-Method_Code,m 是样本数,n 是特征数。
关于def calc_e_Gx(trainDataArr, trainLabelArr, n, div, rule, D):
Gx列表保存对当前所有样本的预测结果。
关于def createSigleBoostingTree(trainDataArr, trainLabelArr, D):
因为代码对样本特征取值进行过简化,特征取值只有0和1,所以
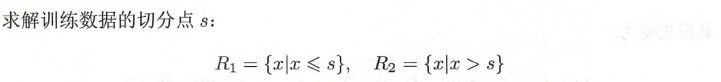
这一步s只有[-0.5, 0.5, 1.5]这几种选择。
同时对上式 R 1 , R 2 R_1,R_2 R1,R2 所预测的类别也进行了探索,用 rule 变量表示。
对每一个特征进行遍历,寻找用于划分的最合适的特征,最终预测误差、最优划分点、划分规则、预测结果、最合适的特征的索引会保存在字典sigleBoostTree中。
pytorch
tensorflow
keras
pytorch API:
tensorflow API
这篇关于电信保温杯笔记——《统计学习方法(第二版)——李航》第8章 提升方法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



