本文主要是介绍电信保温杯笔记——《统计学习方法(第二版)——李航》第7章 支持向量机,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
电信保温杯笔记——《统计学习方法(第二版)——李航》第7章 支持向量机
- 论文
- 介绍
- 数学基础
- 拉格朗日对偶性
- 线性可分的数据集的线性支持向量机
- 线性可分的数据集的线性支持向量机的定义
- 函数间隔和几何间隔
- 函数间隔的定义
- 几何间隔的定义
- 函数间隔与几何间隔的关系
- 间隔最大化
- 最大间隔的超平面
- 步骤
- 最大间隔的超平面的唯一性证明
- 支持向量和间隔边界
- 支持向量的定义
- 间隔边界的定义
- 例子
- 支持向量机的求解:拉格朗日对偶性
- 步骤
- 例子
- 线性不可分的数据集的线性支持向量机
- 线性不可分的数据集的线性支持向量机的定义
- 支持向量机的求解:拉格朗日对偶性
- 步骤
- 支持向量
- 合页损失函数
- 线性不可分的数据集的非线性支持向量机
- 核技巧
- 核函数的定义
- 例子
- 核技巧在支持向量机中的应用
- 正定核
- 正定核的充要条件
- 常用核函数
- 多项式核函数( polynomial kernel function)
- 高斯核函数(Gaussian kernel function)
- 字符串核函数( string kernel function)
- 非线性支持向量机的定义
- 步骤
- 序列最小最优化算法
- 两个变量二次规划的求解方法
- 变量的选择方法
- 1. 第1个变量的选择
- 2. 第2个变量的选择
- 3. 计算阈值 b b b 和差值 E i E_i Ei
- 步骤
- 本章概要
- 相关视频
- 相关的笔记
- 相关代码
- pytorch
- tensorflow
- keras
- pytorch API:
- tensorflow API
论文
线性不可分的数据集的线性支持向量机:《Support-vector networks》
非线性支持向量机:《A training algorithm for optimal margin classifiers》
SMO算法:《Fast training support vector machines using parallel sequential minimal optimization》
介绍
电信保温杯笔记——《统计学习方法(第二版)——李航》
本文是对原书的精读,会有大量原书的截图,同时对书上不详尽的地方进行细致解读与改写。
支持向量机(support vector machines,SVM)是一种二类分类模型。它的基本模型是定义在特征空间上的线性分类器,要求特征空间上正例和负例的间隔最大,是感知机的一种特殊情况;支持向量机还包括核技巧,使它成为非线性分类器。支持向量机的学习策略就是间隔最大化,可形式化为一个求解凸二次规划(convex quadratic programming)的问题,也等价于正则化的合页损失函数的最小化问题。
支持向量机学习方法包含构建由简至繁的模型:
- 线性可分的数据集的线性支持向量机(linearsupport vector machine in linearly separable case):当训练数据线性可分时,通过硬间隔最大化(hard margin maximization),学习一个线性的分类器,即线性可分支持向量机,又称为硬间隔支持向量机;
- 线性不可分的数据集的线性支持向量机(linear supportvector machine):当训练数据线性不可分且只有少部分数据线性不可分时,通过软间隔最大化(soft margin maximization),学习一个线性的分类器,即线性支持向量机,又称为软间隔支持向量机;
- 线性不可分的数据集的非线性支持向量机(non-linear support vector machine):当训练数据线性不可分时,通过使用核技巧(kernel trick)及软间隔最大化,学习非线性支持向量机。
假设输入空间与特征空间为两个不同的空间。输入空间为欧氏空间或离散集合,特征空间为欧氏空间或希尔伯特空间。线性可分的数据集的线性支持向量机、线性不可分的数据集的线性支持向量机假设输入空间与特征空间的元素一一对应,并将输入空间中的输入映射为特征空间中的特征向量。非线性支持向量机利用一个从输入空间到特征空间的非线性映射将输入映射为特征向量。所以,输入都由输入空间转换到特征空间,支持向量机的学习是在特征空间进行的。

数学基础
拉格朗日对偶性
本书的附录C。
“拉格朗日对偶问题”如何直观理解?“KKT条件” “Slater条件” “凸优化”打包理解,这个视频讲解得非常直观。
线性可分的数据集的线性支持向量机

定义2.2:


线性可分的数据集的线性支持向量机的定义


函数间隔和几何间隔

函数间隔的定义



点到平面的距离公式:
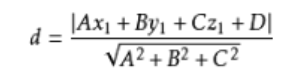


几何间隔的定义

函数间隔与几何间隔的关系

间隔最大化

最大间隔的超平面

到目前为止,超平面的解不是唯一的,但它的解却有无穷多个。

令 γ ^ = 1 \hat{\gamma} = 1 γ^=1 就相对于给了一个约束, w , b w,b w,b 不能再按比例改变了,此时超平面的解是唯一的。
min w , b 1 2 ∥ w ∥ 2 ( 7.13 ) s . t . 1 − y i ( w ⋅ x i + b ) ≤ 0 , i = 1 , 2 , . . . , N ( 7.14 ) \begin{aligned} &\underset {w,b}{\operatorname {min} } \quad \frac{1}{2}\rVert w \rVert^2 \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad (7.13)\\ &s.t. \quad 1 - y_i(w \cdot x_i + b) \leq 0 , i = 1,2,...,N \quad (7.14) \end{aligned} w,bmin21∥w∥2(7.13)s.t.1−yi(w⋅xi+b)≤0,i=1,2,...,N(7.14)

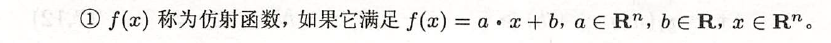

步骤


下面的唯一性证明感觉没有必要看。
最大间隔的超平面的唯一性证明


支持向量和间隔边界
支持向量的定义




间隔边界的定义


例子


支持向量机的求解:拉格朗日对偶性

min w , b 1 2 ∥ w ∥ 2 ( 7.13 ) s . t . 1 − y i ( w ⋅ x i + b ) ≤ 0 , i = 1 , 2 , . . . , N ( 7.14 ) \begin{aligned} &\underset {w,b}{\operatorname {min} } \quad \frac{1}{2}\rVert w \rVert^2 \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad (7.13)\\ &s.t. \quad 1 - y_i(w \cdot x_i + b) \leq 0 , i = 1,2,...,N \quad (7.14) \end{aligned} w,bmin21∥w∥2(7.13)s.t.1−yi(w⋅xi+b)≤0,i=1,2,...,N(7.14)

w , x w,x w,x 都是列向量, w ⋅ x w \cdot x w⋅x 指的是向量的点积, w T x w^T x wTx 指的是向量相乘,两个表示在本文中都是一样的,但后者在求导运算上会更加合适,所以下文有时候会对这种地方进行改写。
L ( w , b , α ) = 1 2 ∥ w ∥ 2 + ∑ i = 1 N α i ( 1 − y i ( w T x i + b ) ) ( 7.18 ) L(w,b,\alpha) = \frac{1}{2}\rVert w \rVert^2 +\sum\limits_{i = 1}^N \alpha_i \left( 1-y_i(w^T x_i + b) \right) \quad (7.18) L(w,b,α)=21∥w∥2+i=1∑Nαi(1−yi(wTxi+b))(7.18)

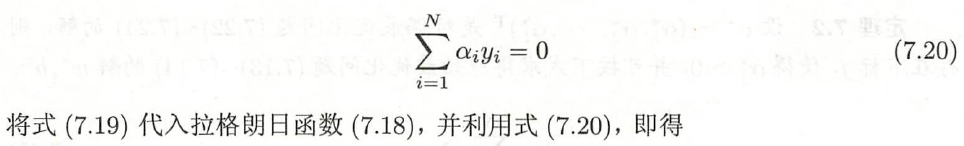
L ( w , b , α ) = 1 2 ∥ w ∥ 2 + ∑ i = 1 N α i ( 1 − y i ( w T x i + b ) ) = 1 2 w T w + ∑ i = 1 N α i ( 1 − y i ( w T x i + b ) ) = 1 2 ∑ i = 1 N α i y i x i T ∑ j = 1 N α j y j x j + ∑ i = 1 N α i ( 1 − y i ( ∑ j = 1 N α j y j x j T x i + b ) ) = 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j x i T x j + ∑ i = 1 N α i − ∑ i = 1 N ∑ j = 1 N α i α j y i y j x i T x j + b ∑ i = 1 N α i y i = − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j x i T x j + ∑ i = 1 N α i \begin{aligned} L(w,b,\alpha) &= \frac{1}{2}\rVert w \rVert^2 +\sum\limits_{i = 1}^N \alpha_i \left( 1-y_i(w^T x_i + b) \right) \\ &= \frac{1}{2} w^Tw + \sum\limits_{i = 1}^N \alpha_i \left( 1-y_i(w^T x_i + b) \right) \\ &= \frac{1}{2} \sum\limits_{i = 1}^N \alpha_iy_ix_i^T \sum\limits_{j = 1}^N \alpha_jy_jx_j + \sum\limits_{i = 1}^N \alpha_i \left( 1-y_i(\sum\limits_{j = 1}^N \alpha_jy_jx_j^T x_i + b) \right) \\ &= \frac{1}{2} \sum\limits_{i = 1}^N \sum\limits_{j = 1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j + \sum\limits_{i = 1}^N \alpha_i -\sum\limits_{i = 1}^N \sum\limits_{j = 1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j + b \sum\limits_{i = 1}^N \alpha_iy_i \\ &= - \frac{1}{2} \sum\limits_{i = 1}^N \sum\limits_{j = 1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j + \sum\limits_{i = 1}^N \alpha_i \end{aligned} L(w,b,α)=21∥w∥2+i=1∑Nαi(1−yi(wTxi+b))=21wTw+i=1∑Nαi(1−yi(wTxi+b))=21i=1∑NαiyixiTj=1∑Nαjyjxj+i=1∑Nαi(1−yi(j=1∑NαjyjxjTxi+b))=21i=1∑Nj=1∑NαiαjyiyjxiTxj+i=1∑Nαi−i=1∑Nj=1∑NαiαjyiyjxiTxj+bi=1∑Nαiyi=−21i=1∑Nj=1∑NαiαjyiyjxiTxj+i=1∑Nαi
即
min w , b L ( w , b , α ) = − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j x i T x j + ∑ i = 1 N α i \underset {w,b}{\operatorname {min} } \, L(w,b,\alpha) = - \frac{1}{2} \sum\limits_{i = 1}^N \sum\limits_{j = 1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j + \sum\limits_{i = 1}^N \alpha_i w,bminL(w,b,α)=−21i=1∑Nj=1∑NαiαjyiyjxiTxj+i=1∑Nαi

上述求解过程可以归结为下面定理:



步骤



例子


线性不可分的数据集的线性支持向量机


min w , b , ξ 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i ( 7.32 ) s . t . 1 − ξ i − y i ( w ⋅ x i + b ) ≤ 0 , i = 1 , 2 , . . . , N ( 7.33 ) − ξ i ≤ 0 , i = 1 , 2 , . . . , N ( 7.34 ) \begin{aligned} &\underset {w,b,\xi}{\operatorname {min} } \quad \frac{1}{2}\rVert w \rVert^2 + C\sum\limits_{i = 1}^N \xi_i \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\,\,\, (7.32)\\ &s.t. \quad 1 - \xi_i - y_i(w \cdot x_i + b) \leq 0 , i = 1,2,...,N \quad (7.33) \\ & \quad\quad\, - \xi_i \leq 0 , i = 1,2,...,N \quad\quad\quad\quad\quad\quad\quad\quad\,\,\, (7.34) \\ \end{aligned} w,b,ξmin21∥w∥2+Ci=1∑Nξi(7.32)s.t.1−ξi−yi(w⋅xi+b)≤0,i=1,2,...,N(7.33)−ξi≤0,i=1,2,...,N(7.34)

这个 b b b 的解可能不唯一暂时没想明白。

线性不可分的数据集的线性支持向量机的定义

支持向量机的求解:拉格朗日对偶性

原始问题(7.32)~(7.34)
min w , b , ξ 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i ( 7.32 ) s . t . 1 − ξ i − y i ( w ⋅ x i + b ) ≤ 0 , i = 1 , 2 , . . . , N ( 7.33 ) − ξ i ≤ 0 , i = 1 , 2 , . . . , N ( 7.34 ) \begin{aligned} &\underset {w,b,\xi}{\operatorname {min} } \quad \frac{1}{2}\rVert w \rVert^2 + C\sum\limits_{i = 1}^N \xi_i \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\,\,\, (7.32)\\ &s.t. \quad 1 - \xi_i - y_i(w \cdot x_i + b) \leq 0 , i = 1,2,...,N \quad (7.33) \\ & \quad\quad\, - \xi_i \leq 0 , i = 1,2,...,N \quad\quad\quad\quad\quad\quad\quad\quad\,\,\, (7.34) \\ \end{aligned} w,b,ξmin21∥w∥2+Ci=1∑Nξi(7.32)s.t.1−ξi−yi(w⋅xi+b)≤0,i=1,2,...,N(7.33)−ξi≤0,i=1,2,...,N(7.34)
原始最优化问题(7.32)~(7.34)的拉格朗日函数是
L ( w , b , ξ , α , μ ) = 1 2 ∥ w ∥ 2 + C ∑ i = 1 N ξ i + ∑ i = 1 N α i ( 1 − ξ i − y i ( w T x i + b ) ) − ∑ i = 1 N μ i ξ i = 1 2 w T w + C ∑ i = 1 N ξ i + ∑ i = 1 N α i ( 1 − ξ i − y i ( w T x i + b ) ) − ∑ i = 1 N μ i ξ i ( 7.40 ) \begin{aligned} L(w,b,\xi,\alpha,\mu) &= \frac{1}{2}\rVert w \rVert^2 + C\sum\limits_{i = 1}^N\xi_i +\sum\limits_{i = 1}^N \alpha_i \left( 1 - \xi_i -y_i(w^T x_i + b) \right) - \sum\limits_{i = 1}^N \mu_i \xi_i \quad \\ &= \frac{1}{2} w^Tw + C\sum\limits_{i = 1}^N\xi_i +\sum\limits_{i = 1}^N \alpha_i \left( 1 - \xi_i -y_i(w^T x_i + b) \right) - \sum\limits_{i = 1}^N \mu_i \xi_i \quad (7.40) \end{aligned} L(w,b,ξ,α,μ)=21∥w∥2+Ci=1∑Nξi+i=1∑Nαi(1−ξi−yi(wTxi+b))−i=1∑Nμiξi=21wTw+Ci=1∑Nξi+i=1∑Nαi(1−ξi−yi(wTxi+b))−i=1∑Nμiξi(7.40)
其中, α i ≥ 0 , μ i ≥ 0 \alpha_i \geq 0, \mu_i \geq 0 αi≥0,μi≥0。

L ( w , b , ξ , α , μ ) = 1 2 w T w + C ∑ i = 1 N ξ i + ∑ i = 1 N α i ( 1 − ξ i − y i ( w T x i + b ) ) − ∑ i = 1 N μ i ξ i = 1 2 ∑ i = 1 N α i y i x i T ∑ j = 1 N α j y j x j + C ∑ i = 1 N ξ i + ∑ i = 1 N α i ( 1 − ξ i − y i ( ∑ j = 1 N α j y j x j T x i + b ) ) − ∑ i = 1 N μ i ξ i = 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j x i T x j + ∑ i = 1 N ( C − α i − μ i ) ξ i + ∑ i = 1 N α i − ∑ i = 1 N ∑ j = 1 N α i α j y i y j x i T x j + b ∑ i = 1 N α i y i = − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j x i T x j + ∑ i = 1 N α i \begin{aligned} L(w,b,\xi,\alpha,\mu) &= \frac{1}{2} w^Tw + C\sum\limits_{i = 1}^N\xi_i +\sum\limits_{i = 1}^N \alpha_i \left( 1 - \xi_i -y_i(w^T x_i + b) \right) - \sum\limits_{i = 1}^N \mu_i \xi_i \\ &= \frac{1}{2} \sum\limits_{i = 1}^N \alpha_iy_ix_i^T \sum\limits_{j = 1}^N \alpha_jy_jx_j + C\sum\limits_{i = 1}^N\xi_i + \sum\limits_{i = 1}^N \alpha_i \left( 1 - \xi_i -y_i(\sum\limits_{j = 1}^N \alpha_jy_jx_j^T x_i + b) \right) - \sum\limits_{i = 1}^N \mu_i \xi_i \\ &= \frac{1}{2} \sum\limits_{i = 1}^N \sum\limits_{j = 1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j + \sum\limits_{i = 1}^N (C - \alpha_i - \mu_i) \xi_i + \sum\limits_{i = 1}^N \alpha_i -\sum\limits_{i = 1}^N \sum\limits_{j = 1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j + b \sum\limits_{i = 1}^N \alpha_iy_i \\ &= - \frac{1}{2} \sum\limits_{i = 1}^N \sum\limits_{j = 1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j + \sum\limits_{i = 1}^N \alpha_i \end{aligned} L(w,b,ξ,α,μ)=21wTw+Ci=1∑Nξi+i=1∑Nαi(1−ξi−yi(wTxi+b))−i=1∑Nμiξi=21i=1∑NαiyixiTj=1∑Nαjyjxj+Ci=1∑Nξi+i=1∑Nαi(1−ξi−yi(j=1∑NαjyjxjTxi+b))−i=1∑Nμiξi=21i=1∑Nj=1∑NαiαjyiyjxiTxj+i=1∑N(C−αi−μi)ξi+i=1∑Nαi−i=1∑Nj=1∑NαiαjyiyjxiTxj+bi=1∑Nαiyi=−21i=1∑Nj=1∑NαiαjyiyjxiTxj+i=1∑Nαi
即
min w , b , ξ L ( w , b , ξ , α , μ ) = − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j x i T x j + ∑ i = 1 N α i \underset {w,b,\xi }{\operatorname {min} } \, L(w,b,\xi,\alpha,\mu) = - \frac{1}{2} \sum\limits_{i = 1}^N \sum\limits_{j = 1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j + \sum\limits_{i = 1}^N \alpha_i w,b,ξminL(w,b,ξ,α,μ)=−21i=1∑Nj=1∑NαiαjyiyjxiTxj+i=1∑Nαi


将上述过程记为如下定理:


步骤

这是一个落在间隔边界上的点,与线性可分的数据集的线性支持向量机求解 b b b 时相同。

支持向量


min w , b , ξ L ( w , b , ξ , α , μ ) = 1 2 w T w + C ∑ i = 1 N ξ i + ∑ i = 1 N α i ( 1 − ξ i − y i ( w T x i + b ) ) − ∑ i = 1 N μ i ξ i s . t . 1 − ξ i − y i ( w ⋅ x i + b ) ≤ 0 , i = 1 , 2 , . . . , N − ξ i ≤ 0 , i = 1 , 2 , . . . , N α i ≥ 0 , i = 1 , 2 , . . . , N μ i ≥ 0 , i = 1 , 2 , . . . , N C − α i − μ i = 0 , i = 1 , 2 , . . . , N C > 0 \begin{aligned} & \underset {w,b,\xi }{\operatorname {min} } \, L(w,b,\xi,\alpha,\mu) = \frac{1}{2} w^Tw + C\sum\limits_{i = 1}^N\xi_i +\sum\limits_{i = 1}^N \alpha_i \left( 1 - \xi_i -y_i(w^T x_i + b) \right) - \sum\limits_{i = 1}^N \mu_i \xi_i \\ &s.t. \quad 1 - \xi_i - y_i(w \cdot x_i + b) \leq 0 , i = 1,2,...,N \\ & \quad\quad\, - \xi_i \leq 0 , i = 1,2,...,N \\ & \quad\quad\, \alpha_i \geq 0 , i = 1,2,...,N \\ & \quad\quad\, \mu_i \geq 0 , i = 1,2,...,N \\ & \quad\quad\, C - \alpha_i - \mu_i = 0 , i = 1,2,...,N \\ & \quad\quad\, C > 0 \end{aligned} w,b,ξminL(w,b,ξ,α,μ)=21wTw+Ci=1∑Nξi+i=1∑Nαi(1−ξi−yi(wTxi+b))−i=1∑Nμiξis.t.1−ξi−yi(w⋅xi+b)≤0,i=1,2,...,N−ξi≤0,i=1,2,...,Nαi≥0,i=1,2,...,Nμi≥0,i=1,2,...,NC−αi−μi=0,i=1,2,...,NC>0
以正例为例:
| 点 | 类型 | y i ( w T x i + b ) y_i(w^T x_i + b) yi(wTxi+b) | α i \alpha_i αi | ξ i \xi_i ξi | μ i \mu_i μi | 位置 |
|---|---|---|---|---|---|---|
| 取值范围 | ≥ 1 − ξ i \geq 1 - \xi_i ≥1−ξi | 0 ≤ α i ≤ C 0 \leq \alpha_i \leq C 0≤αi≤C | ≥ 0 \geq 0 ≥0 | ≥ 0 \geq 0 ≥0 | ||
| A | 支持向量 | = 1 − ξ i = 1 - \xi_i =1−ξi | 0 < α i < C 0<\alpha_i <C 0<αi<C,约束 | = 0 =0 =0 | 0 < μ i < C 0<\mu_i < C 0<μi<C,约束 | 在软间隔边界上 |
| B | 支持向量 | = 1 − ξ i = 1 - \xi_i =1−ξi | = C =C =C,约束 | 0 < ξ i < 1 0<\xi_i <1 0<ξi<1 | = 0 =0 =0,松弛 | 在软间隔边界与分离超平面之间 |
| C | 支持向量 | = 1 − ξ i = 1 - \xi_i =1−ξi | = C =C =C,约束 | > 1 >1 >1 | = 0 =0 =0,松弛 | 在分离超平面误分一侧 |
| D | 非支持向量 | > 1 − ξ i > 1 - \xi_i >1−ξi | = 0 =0 =0,松弛 | = 0 =0 =0 | 0 < μ i < C 0<\mu_i < C 0<μi<C,约束 | 正确分类且在软间隔之外 |
合页损失函数

下面定理说明线性不可分的数据集的线性支持向量机求解等价于其关于合页损失函数+正则化的优化问题的求解:


不同位置的点造成的损失为:

线性不可分的数据集的非线性支持向量机

核技巧


核函数的定义

例子

核技巧在支持向量机中的应用


正定核

其实在机器学习,深度学习这一块,经常会用到向量空间的概念,这里涉及矩阵分析的一些概念,其中最常见的无非就是线性空间,内积空间,空间上两点间距离这几个概念。我们平时使用的这些概念,通常都是在欧氏空间上使用,比如加减乘、点积、2点间距离,但如果我们使用的空间不再是欧氏空间,而是其他空间,那么我们就要定义元素、向量在这些空间上的运算法则,下面那段话中的第一句,就是为上述概念的运算法则提供保障的。

以下是定义在这些构造的空间上的运算法则。不看其实具体证明其实也没什么关系,只需知道它就是定义了一个新的内积运算,用这个新内积运算去代替下面公式中的 x i T ⋅ x j x_i^T \cdot x_j xiT⋅xj,从而得到非线性运算的支持向量机。可以直接跳到序列最小最优化算法的部分。
min w , b , ξ L ( w , b , ξ , α , μ ) = − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j x i T x j + ∑ i = 1 N α i \underset {w,b,\xi }{\operatorname {min} } \, L(w,b,\xi,\alpha,\mu) = - \frac{1}{2} \sum\limits_{i = 1}^N \sum\limits_{j = 1}^N \alpha_i \alpha_j y_i y_j x_i^T x_j + \sum\limits_{i = 1}^N \alpha_i w,b,ξminL(w,b,ξ,α,μ)=−21i=1∑Nj=1∑NαiαjyiyjxiTxj+i=1∑Nαi



正定核的充要条件


常用核函数
多项式核函数( polynomial kernel function)

高斯核函数(Gaussian kernel function)

字符串核函数( string kernel function)


如上所述,利用核技巧,可以将线性分类的学习方法应用到非线性分类问题中去。将线性支持向量机扩展到非线性支持向量机,只需将线性支持向量机对偶形式中的内积换成核函数。
非线性支持向量机的定义

步骤

序列最小最优化算法
先看这个视频,再看书上的推导:快速理解SMO算法


两个变量二次规划的求解方法
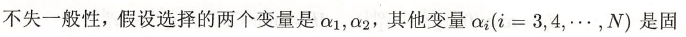

观察公式(7.101)和(7.102)可知, K 11 , K 22 > 0 K_{11},K_{22} > 0 K11,K22>0, α 1 = ς y 1 − α 2 y 1 y 2 \alpha_1 = \varsigma y_1 - \alpha_2 y_1y_2 α1=ςy1−α2y1y2,将(7.102)带入(7.101)必然得到关于 α 2 \alpha_2 α2 的一元二次函数 f ( α 2 ) f(\alpha_2) f(α2),且开口向上:
f ( α 2 ) = a ⋅ α 2 2 + b ⋅ α 2 + c , a > 0 f(\alpha_2) = a\cdot \alpha_2^2 + b \cdot \alpha_2 + c,a>0 f(α2)=a⋅α22+b⋅α2+c,a>0
此时(7.102)这个子问题的最小值变成求一元二次函数 f ( α 2 ) f(\alpha_2) f(α2)的最小值了,接下来问题的关键就在于 α 2 \alpha_2 α2 的定义域了。令 ς y 1 = k \varsigma y_1 = k ςy1=k,
当 y 1 = y 2 = 1 y_1 = y_2 = 1 y1=y2=1 时,
α 1 = ς y 1 − α 2 y 1 y 2 = k − α 2 , ∵ α 1 ∈ [ 0 , C ] , α 2 = k − α 1 , ∴ α 2 ∈ [ k − C , k ] , 又 ∵ α 2 ∈ [ 0 , C ] , ∴ α 2 ∈ [ m a x { k − C , 0 } , m i n { k , C } ] , 又 ∵ k = α 1 + α 2 , ∴ α 2 ∈ [ m a x { α 1 + α 2 − C , 0 } , m i n { α 1 + α 2 , C } ] . \begin{aligned} & \alpha_1 = \varsigma y_1 - \alpha_2 y_1y_2 = k - \alpha_2, \\ & \because \alpha_1 \in [0,C], \alpha_2 = k - \alpha_1, \\ & \therefore \alpha_2 \in [k - C,k], \\ & \text{又} \because \alpha_2 \in [0,C], \\ & \therefore \alpha_2 \in [ max\{k - C, 0\} , min\{k , C\} ], \\ & \text{又} \because k = \alpha_1 + \alpha_2, \\ & \therefore \alpha_2 \in [ max\{\alpha_1 + \alpha_2 - C, 0\} , min\{\alpha_1 + \alpha_2 , C\} ]. \end{aligned} α1=ςy1−α2y1y2=k−α2,∵α1∈[0,C],α2=k−α1,∴α2∈[k−C,k],又∵α2∈[0,C],∴α2∈[max{k−C,0},min{k,C}],又∵k=α1+α2,∴α2∈[max{α1+α2−C,0},min{α1+α2,C}].
记 L = m a x { α 1 + α 2 − C , 0 } , H = m i n { α 1 + α 2 , C } L = max\{\alpha_1 + \alpha_2 - C, 0\}, H = min\{\alpha_1 + \alpha_2 , C\} L=max{α1+α2−C,0},H=min{α1+α2,C}。
当 y 1 ≠ y 2 y_1 \neq y_2 y1=y2 时,
α 1 = ς y 1 − α 2 y 1 y 2 = k + α 2 , ∵ α 1 ∈ [ 0 , C ] , α 2 = α 1 − k , ∴ α 2 ∈ [ − k , C − k ] , 又 ∵ α 2 ∈ [ 0 , C ] , ∴ α 2 ∈ [ m a x { − k , 0 } , m i n { C − k , C } ] , 又 ∵ k = α 1 − α 2 , ∴ α 2 ∈ [ m a x { α 2 − α 1 , 0 } , m i n { C + α 2 − α 1 , C } ] . \begin{aligned} & \alpha_1 = \varsigma y_1 - \alpha_2 y_1y_2 = k + \alpha_2, \\ & \because \alpha_1 \in [0,C], \alpha_2 = \alpha_1 - k, \\ & \therefore \alpha_2 \in [-k, C - k], \\ & \text{又} \because \alpha_2 \in [0,C], \\ & \therefore \alpha_2 \in [ max\{-k, 0\} , min\{C - k , C\} ], \\ & \text{又} \because k = \alpha_1 - \alpha_2, \\ & \therefore \alpha_2 \in [ max\{\alpha_2 - \alpha_1 , 0\} , min\{C + \alpha_2 - \alpha_1 , C\} ]. \end{aligned} α1=ςy1−α2y1y2=k+α2,∵α1∈[0,C],α2=α1−k,∴α2∈[−k,C−k],又∵α2∈[0,C],∴α2∈[max{−k,0},min{C−k,C}],又∵k=α1−α2,∴α2∈[max{α2−α1,0},min{C+α2−α1,C}].
记 L = m a x { α 2 − α 1 , 0 } , H = m i n { C + α 2 − α 1 , C } L = max\{\alpha_2 - \alpha_1 , 0\}, H = min\{C + \alpha_2 - \alpha_1 , C\} L=max{α2−α1,0},H=min{C+α2−α1,C}。
此时, α 2 ∈ [ L , H ] \alpha_2 \in [ L , H ] α2∈[L,H]。我们知道一元二次函数 f ( α 2 ) f(\alpha_2) f(α2)在不考虑定义域时,最小值时的 α 2 \alpha_2 α2 是很容易求出的,记此时的 α 2 \alpha_2 α2 为 α 2 n e w , u n c \alpha_2^{new,unc} α2new,unc,缩写为:new,unclip,而考虑定义域时,一元二次函数 f ( α 2 ) f(\alpha_2) f(α2) 取得最小值时的 α 2 \alpha_2 α2 记为 α 2 n e w \alpha_2^{new} α2new,下图展示了各种情况时的变量关系:



上述过程可以记为如下定理:



变量的选择方法
SMO 算法在每个子问题中选择两个变量优化,其中至少一个变量是违反KKT条件的。
1. 第1个变量的选择

以正例点为例:
点 | 类型 | y i ( w T x i + b ) y_i(w^T x_i + b) yi(wTxi+b) | α i \alpha_i αi | ξ i \xi_i ξi | μ i \mu_i μi | 位置
-------- | ----- | ----- | ----- | ----- | ----- | ----- | -----
取值范围 | | ≥ 1 − ξ i \geq 1 - \xi_i ≥1−ξi | 0 ≤ α i ≤ C 0 \leq \alpha_i \leq C 0≤αi≤C| ≥ 0 \geq 0 ≥0 | ≥ 0 \geq 0 ≥0 |
A | 支持向量 | = 1 − ξ i = 1 - \xi_i =1−ξi | 0 < α i < C 0<\alpha_i <C 0<αi<C,约束 | = 0 =0 =0 | 0 < μ i < C 0<\mu_i < C 0<μi<C,约束 | 在软间隔边界上
B | 支持向量 | = 1 − ξ i = 1 - \xi_i =1−ξi | = C =C =C,约束 | 0 < ξ i < 1 0<\xi_i <1 0<ξi<1 | = 0 =0 =0,松弛 | 在软间隔边界与分离超平面之间
C | 支持向量 | = 1 − ξ i = 1 - \xi_i =1−ξi | = C =C =C,约束 | > 1 >1 >1 | = 0 =0 =0,松弛 | 在分离超平面误分一侧
D | 非支持向量 | > 1 − ξ i > 1 - \xi_i >1−ξi | = 0 =0 =0,松弛 | = 0 =0 =0 | 0 < μ i < C 0<\mu_i < C 0<μi<C,约束 | 正确分类且在软间隔之外
min w , b , ξ L ( w , b , ξ , α , μ ) = 1 2 w T w + C ∑ i = 1 N ξ i + ∑ i = 1 N α i ( 1 − ξ i − y i ( w T x i + b ) ) − ∑ i = 1 N μ i ξ i s . t . 1 − ξ i − y i ( w ⋅ x i + b ) ≤ 0 , i = 1 , 2 , . . . , N − ξ i ≤ 0 , i = 1 , 2 , . . . , N α i ≥ 0 , i = 1 , 2 , . . . , N μ i ≥ 0 , i = 1 , 2 , . . . , N C − α i − μ i = 0 , i = 1 , 2 , . . . , N C > 0 \begin{aligned} & \underset {w,b,\xi }{\operatorname {min} } \, L(w,b,\xi,\alpha,\mu) = \frac{1}{2} w^Tw + C\sum\limits_{i = 1}^N\xi_i +\sum\limits_{i = 1}^N \alpha_i \left( 1 - \xi_i -y_i(w^T x_i + b) \right) - \sum\limits_{i = 1}^N \mu_i \xi_i \\ &s.t. \quad 1 - \xi_i - y_i(w \cdot x_i + b) \leq 0 , i = 1,2,...,N \\ & \quad\quad\, - \xi_i \leq 0 , i = 1,2,...,N \\ & \quad\quad\, \alpha_i \geq 0 , i = 1,2,...,N \\ & \quad\quad\, \mu_i \geq 0 , i = 1,2,...,N \\ & \quad\quad\, C - \alpha_i - \mu_i = 0 , i = 1,2,...,N \\ & \quad\quad\, C > 0 \end{aligned} w,b,ξminL(w,b,ξ,α,μ)=21wTw+Ci=1∑Nξi+i=1∑Nαi(1−ξi−yi(wTxi+b))−i=1∑Nμiξis.t.1−ξi−yi(w⋅xi+b)≤0,i=1,2,...,N−ξi≤0,i=1,2,...,Nαi≥0,i=1,2,...,Nμi≥0,i=1,2,...,NC−αi−μi=0,i=1,2,...,NC>0


2. 第2个变量的选择

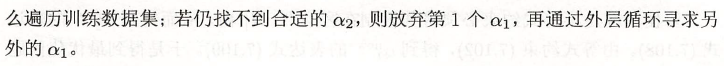
3. 计算阈值 b b b 和差值 E i E_i Ei

步骤

本章概要




相关视频
快速理解SMO算法
相关的笔记
hktxt /Learn-Statistical-Learning-Method
相关代码
Dod-o /Statistical-Learning-Method_Code
关于def isSatisfyKKT(self, i):
toler变量是SMO算法第1个变量的选择中的检验参数 ϵ \epsilon ϵ 。
math.fabs(self.alpha[i]) < self.toler 等价于 α i = 0 \alpha_i = 0 αi=0;
math.fabs(self.alpha[i] - self.C) < self.toler 等价于 α i = C \alpha_i = C αi=C;
self.alpha[i] > -self.toler) and (self.alpha[i] < (self.C + self.toler 等价于 0 < α i < C 0 < \alpha_i < C 0<αi<C;

pytorch
tensorflow
keras
pytorch API:
tensorflow API
这篇关于电信保温杯笔记——《统计学习方法(第二版)——李航》第7章 支持向量机的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




