本文主要是介绍Codeforces848B Rooter's Song,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Rooter's Song
Wherever the destination is, whoever we meet, let's render this song together.
On a Cartesian coordinate plane lies a rectangular stage of size w × h, represented by a rectangle with corners (0, 0), (w, 0), (w, h) and (0, h). It can be seen that no collisions will happen before one enters the stage.
On the sides of the stage stand n dancers. The i-th of them falls into one of the following groups:
- Vertical: stands at (xi, 0), moves in positive y direction (upwards);
- Horizontal: stands at (0, yi), moves in positive x direction (rightwards).
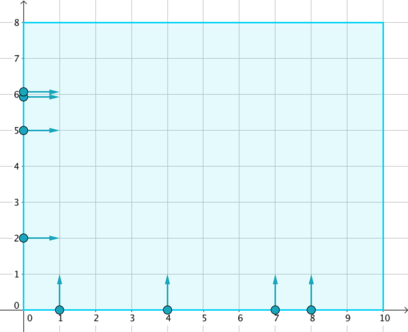
According to choreography, the i-th dancer should stand still for the first ti milliseconds, and then start moving in the specified direction at 1 unit per millisecond, until another border is reached. It is guaranteed that no two dancers have the same group, position and waiting time at the same time.
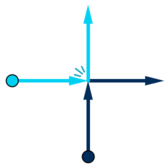
When two dancers collide (i.e. are on the same point at some time when both of them are moving), they immediately exchange their moving directions and go on.
Dancers stop when a border of the stage is reached. Find out every dancer's stopping position.
Input
The first line of input contains three space-separated positive integers n, w and h (1 ≤ n ≤ 100 000, 2 ≤ w, h ≤ 100 000) — the number of dancers and the width and height of the stage, respectively.
The following n lines each describes a dancer: the i-th among them contains three space-separated integers gi, pi, and ti (1 ≤ gi ≤ 2, 1 ≤ pi ≤ 99 999, 0 ≤ ti ≤ 100 000), describing a dancer's group gi (gi = 1 — vertical, gi = 2 — horizontal), position, and waiting time. If gi = 1 then pi = xi; otherwise pi = yi. It's guaranteed that 1 ≤ xi ≤ w - 1 and 1 ≤ yi ≤ h - 1. It is guaranteed that no two dancers have the same group, position and waiting time at the same time.
Output
Output n lines, the i-th of which contains two space-separated integers (xi, yi) — the stopping position of the i-th dancer in the input.
Examples 8 10 8 1 1 10 1 4 13 1 7 1 1 8 2 2 2 0 2 5 14 2 6 0 2 6 1 output 4 8 10 5 8 8 10 6 10 2 1 8 7 8 10 6 input 3 2 3 1 1 2 2 1 1 1 1 5 output 1 3 2 1 1 3
Note
The first example corresponds to the initial setup in the legend, and the tracks of dancers are marked with different colours in the following figure.
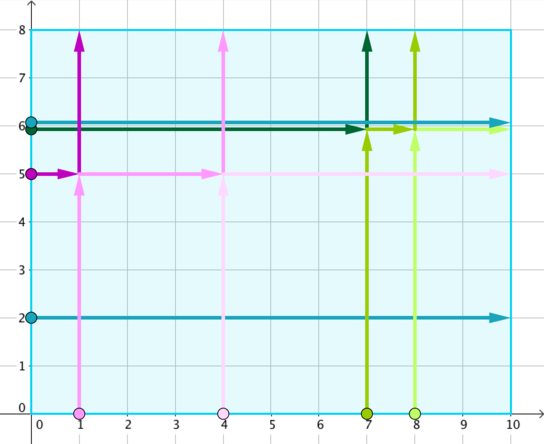
In the second example, no dancers collide.
题意:有一些点会以1格每秒的速度向前运动,这些点从x轴或者y轴上出发,如果他们相遇了则会按上示意图所示进行调转方向。
问这些点最后的落到的坐标是什么。
解法:思维 & 排序
首先考虑在什么情况下两个点会相遇,经过简单的思考发现当坐标减去时间值相等时两者会相遇。
我们可以做这样的一个处理,如果是x轴的点,将其纵坐标记为-t;如果是y轴的点,将其横坐标记为-t。
这样便可以将所有点看作是同时出发的点了。
x+y相等的点就是会相撞的,他们的终点位置会发生一些交换。
x+y相等的起点是在一条直线上,每个点撞来撞去其实守住了自己的相对位置,上面的还是在上面,左边的还是在左边。所以分别对应了一样排序好的终点位置。
所以我们要做的是:结构体存储原始坐标、index、终点坐标
将起点进行排序,如果两个点不会相撞,则按x0+y0进行排序,否则按x0-y0进行排序
复制一份一样的点,再排序一次,这一次是对终点进行排序,如果x0+y0相等,则按x1-y1排序
这样能够保证不碰撞的点始终位置不变,碰撞的点位置按原来的上下左右关系排列。(这里可能要稍微理解一下)
#include <bits/stdc++.h>
#include <cstdio>
#define ll long long
#define __max(a,b) a > b ? a : b
#define pll pair<ll, ll>
using namespace std;
const int maxn = 1e5 + 10;
struct node
{int idx, x0, y0;int x1, y1;
};
node a[maxn], b[maxn];
bool cmp1 (const node &a, const node &b)//对初始坐标进行排序
{if(a.x0 + a.y0 == b.x0 + b.y0)return a.x0 < b.x0; //只要x小就可以了return a.x0 + a.y0 > b.x0 + b.y0;
}
bool cmp2 (const node &a, const node &b)//对终点进行排序
{if(a.x0 + a.y0 == b.x0 + b.y0){
// return a.x1 - a.y1 < b.x1 - b.y1;//两者都行return a.x1 < b.x1 || a.y1 > b.y1;//两者都行}return a.x0 + a.y0 > b.x0 + b.y0;
}
int ax[maxn], ay[maxn];
int main()
{
// freopen("/Users/vector/Desktop/out.txt", "w", stdout);ios::sync_with_stdio(false);cin.tie(0);int n, w, h;cin >> n >> w >> h;int g, p, t;for(int i = 0; i < n; i++){cin >> g >> p >> t;if(g == 1){a[i] = node{i, p, -t, p, h};b[i] = a[i];}else{a[i] = node{i, -t, p, w, p};b[i] = a[i];}}sort(a, a + n, cmp1);//对起点进行排序sort(b, b + n, cmp2);//对终点进行排序for(int i = 0; i < n; i++){ax[a[i].idx] = b[i].x1;ay[a[i].idx] = b[i].y1;}for(int i = 0; i < n; i++)cout << ax[i] << ' ' << ay[i] << endl;return 0;
}
这篇关于Codeforces848B Rooter's Song的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






