手搓B-树 全代码实现 算是半自主研发了吧（雾） 以洛谷P1177桶排验证

前言

建议看这篇文章之前先学基本概念和定义。

B-树比起AVL树的实现难度，我觉得是AVL树的两倍，不只是代码长度上的两倍，而且逻辑负担上也是很重的，很难，确实很难，尤其是删除时的策略，坑很多，非常痛苦，我也尝试去找先人的代码，结果大部分都是部分代码，部分逻辑讲解，或者逻辑上存在错误的讲解，B站上似乎也只有原理讲解，所以这篇文章应该是比较完整的B-树的讲解了。

叠甲：要是有问题请提出，毕竟没有用P3369进行检验。

暂时只学了AVL树和B-树，有时间的话再学RB树，搓一下。

推荐一篇文章：

【精选​​​​​​】【C语言】B 树全代码实现与超超详细思路解读（五天的呕心沥血，绝对原创每个细节，详解查找、插入与删除）_b-树 c 实现_寒冰小澈IceClean的博客-CSDN博客

这位博主其实已经讲得很好了，insert函数也确实实现了，但是erase函数逻辑不清晰，考虑不全面，部分想法很天真，实际上是存在很大漏洞的。我跟着这篇博客学习了很久，帮我梳理了删除函数的逻辑，完善了自己的想法，非常感谢其中的打印函数，让我可以快速的debug。

定义

来看定义：

#define m 5struct node
{int key, value;bool operator<(const node &it) const{return key < it.key;}bool operator>(const node &it) const{return key > it.key;}bool operator==(const node &it) const{return key == it.key;}
};struct BTnode
{BTnode *parent = nullptr;int keynum = 0;BTnode *child[m + 1] = {0};node key[m + 1];int Size[m+1]={0};
};struct Result
{BTnode *ptr;bool tag;int i;
};

与 数据结构-严蔚敏 课本上的一致，除了删除了record节点，增加了node节点用来方便桶排检验代码正确性。

class B_Tree
{
private:int Size;BTnode *root;const int key_min = (m - 1) / 2;const int mid = (m + 1) / 2;const int key_max = m - 1;public:B_Tree(){Size = 0;root = nullptr;}

定义，为什么AVL树中选择搞一个头结点，这里却没有呢？显然是没有必要，有没有对代码都没有明显的帮助作用。注意private中 mid表示中间的节点，key_max表示最大节点个数，key_min表示最小节点个数。

辅助函数与查找函数

先看辅助函数：

    int findpos(BTnode *&q, node &x) //作用:找这个节点中第一个大于等于x的下标,PS:永远不可能为0{return lower_bound(q->key + 1, q->key + 1 + q->keynum, x) - q->key;}//    下面三个是调试用打印函数，非常重要！！！/* 计算出整棵树上记录条数的总和 */int CountKeyNum(BTnode *tree){// 空树则为 0if (tree == NULL)return 0;// 计算所有子树记录条数总和int childTotal = 0;for (int i = 0; i <= tree->keynum; i++){childTotal += CountKeyNum(tree->child[i]);}// 子树加上自身的记录条数，即为总记录条数return tree->keynum + childTotal;}/* 打印 B 树 */void TraverseBTree(BTnode *tree = nullptr){ // 看的别人代码直接复制粘贴的调试函数// 动态创建一个数组，用于存放当前结点是否为最后结点的标识tree = this->root;int nowNum = 0;int *isLast = (int *)malloc(sizeof(int) * (CountKeyNum(tree) + 10));// 打印树形printf("\n");PrintBTree(tree, isLast, nowNum);}/* 递归打印树形 */void PrintBTree(BTnode *tree, int isLast[], int nowNum){// 空树直接跳过if (tree == nullptr)return;// 打印新节点先打印一下平台printf("-|\n");for (int i = 0; i <= tree->keynum; i++){if (tree->child[i] != NULL){printBranch(isLast, nowNum);printf("|----");isLast[nowNum++] = (i == tree->keynum);PrintBTree(tree->child[i], isLast, nowNum);nowNum--;}if (i != tree->keynum){printBranch(isLast, nowNum);printf("|- %d\n", tree->key[i + 1].key);}}}/* 打印树枝 */void printBranch(int isLast[], int nowNum){for (int i = 0; i < nowNum; i++){if (isLast[i])printf(" ");elseprintf("|");printf("      ");}}

讲真的，这个打印函数在编代码的帮助真的是非常之多，可以快速用来发现错误。尤其是erase中的调整树型。

先看最简单的search函数：
 

    Result search(int x) // 找位置，函数很简单，没啥好说的{BTnode *p = root, *q = nullptr;int i;bool flag = 0;node key = {x, 1};while (p != nullptr && !flag){i = findpos(p, key);if (i <= p->keynum && p->key[i] == key)flag = 1;else{q = p;p = p->child[i - 1];}}if (flag)//查找成功，返回节点return {p, flag, i};else//查找失败，返回插入节点return {q, flag, i};}

逻辑简单易懂，也没啥好说的，主要是要注意一下 i 表示的范围是 [1,keynum+1] ，这一点在后面很有用。

插入函数

再看insert函数及其辅助函数：

    bool insert(int x){Result res = search(x);if (res.tag) // 找到了，就个数+1{++res.ptr->key[res.i].value;return false;}else//没找到，就插入，{insert(root, {x, 1}, res);++Size;return true;}}void newroot(BTnode *&root, BTnode *&child1, BTnode *&child2, node &key) // 如果根节点出现了分裂或者初始为空,需要新建一个节点，这个时候才会出现这个函数{root = new BTnode;root->keynum = 1;root->key[1] = key;root->child[0] = child1;root->child[1] = child2;root->parent = nullptr;if (child1 != nullptr)child1->parent = root;if (child2 != nullptr)child2->parent = root;return;}void split(BTnode *&p, BTnode *&ap) // p分裂，并分给ap{ap = new BTnode;ap->child[0] = p->child[mid]; // 别忘了for (int i = mid + 1, j = 1; i <= p->keynum; ++i, ++j)//赋值ap->key[j] = p->key[i],ap->child[j] = p->child[i];ap->parent = p->parent;ap->keynum = p->keynum - mid;p->keynum = mid - 1;// 双亲和孩子的双向绑定for (int i = 0; i <= ap->keynum; ++i)if (ap->child[i] != nullptr)ap->child[i]->parent = ap;return;}void InsertBTnode(BTnode *&p, node &key, BTnode *ap) // 给出节点，值和指针，不要给出i！！！不然会变得不幸！{int i = findpos(p, key); // i在这里现场获得！！！for (int j = p->keynum; j >= i; --j)p->key[j + 1] = p->key[j],p->child[j + 1] = p->child[j];p->child[i] = ap;p->key[i] = key;p->keynum++;if (ap != nullptr)//双向绑定ap->parent = p;return;}void insert(BTnode *&root, node key, Result &res) // 插入{BTnode *ap = nullptr, *p = res.ptr;bool finished = false;// int i = res.i;//这个i其实屁用没有，因为我坚持i一定要现场获得，不然会变得不幸！while (p != nullptr && !finished){InsertBTnode(p, key, ap);if (p->keynum <= key_max)finished = 1;else{split(p, ap);key = p->key[mid];if (p->parent != nullptr){p = p->parent;// i = findpos(p, key);//不要管i!!!}elsebreak;}}if (!finished) // finished为空，说明p为根，如果p是根，说明要么根分裂了，要么树为空newroot(root, p, ap, key);}

注意三点：

1.这里可以看到我多次注释，不要管i，也就是位置，把它放在InsertBTnode函数中自己处理，这个原则一定要坚持，换句话说就是函数的接口要尽可能简单，实现的功能可以少，就像AVL树中结构体中不要定义bf一样，只有吃过屎你才知道为什么这么干而不那么干。

2.一定要注意父亲和孩子的双向绑定，不能我能找到你，你找不到我。

3.这一点非常重要，不要着急去写删除函数！！！在这里停下来，因为有了insert函数和search函数就可以用来桶排序了，可以现在洛谷P1177中检验insert函数正确性，还有用打印函数判断B-树的树型是否正确，这非常重要！！！

删除函数

接下来是难中之难，删除函数：

先看完整代码体验一下其恐怖：

    bool erase(int x){Result res = search(x);if (res.tag){if (--res.ptr->key[res.i].value == 0)erase(root, {x, 1}, res);return true;}elsereturn false;}void Merge(BTnode *&left, BTnode *&right) // 把右边归并到左边，并删除右边的节点{for (int i = left->keynum + 1, j = 1; j <= right->keynum; ++j, ++i){left->key[i] = right->key[j];left->child[i] = right->child[j];if (left->child[i] != nullptr) // 把孩子更改父亲left->child[i]->parent = left;++left->keynum;}delete right;right = left;}void Adjust(BTnode *&p) // 调整树型{BTnode *parent = p->parent, *brother;int i;while (p->keynum < key_min && parent != nullptr) // 如果节点个数比较少，同时不为根节点{i = findpos(parent, p->key[1]); // 父亲的编号 当前在 child[i-1] 中if (i > 1 && (brother = parent->child[i - 2]) != nullptr) // 左兄弟不为空， 当前在 child[i-1] 那么 child[i-2]就是左兄弟了{if (brother->keynum > key_min) // 左兄弟富裕{InsertBTnode(p, parent->key[i-1], brother->child[brother->keynum]); // 把父亲的节点要下来，注意把左兄弟最右端的指针也拿下来swap(p->child[0],p->child[1]);brother->child[brother->keynum]=nullptr;// 这里不需要像有兄弟一样把 child[brother->keynum] 置空，因为减1了，画个图就明白了parent->key[i-1] = brother->key[brother->keynum]; // 然后父亲替换成左兄弟的最大值Remove(brother, brother->key[brother->keynum]); // 左兄弟删除这个节点，break;                                          // 调整完成，break}else // 左兄弟穷{InsertBTnode(brother, parent->key[i-1], p->child[0]); // 把父亲要下来，这个时候父亲那个节点要被删除，把兄弟最右端指针拿下来p->child[0]=nullptr;Remove(parent, parent->key[i-1]);           // 删除父亲Merge(brother, p);                        // 合并兄弟p = p->parent; // 父亲可能节点变少，继续循环parent = p->parent;}}else if (i <= parent->keynum && (brother = parent->child[i]) != nullptr) // 有右兄弟{if (brother->keynum > key_min) // 右兄弟富裕{InsertBTnode(p, parent->key[i], brother->child[0]);brother->child[0] = brother->child[1]; // 这一句别忘了多加，因为右兄弟最左端节点被我拿走了，所以附带的他也为空parent->key[i] = brother->key[1];Remove(brother, brother->key[1]);break;}else // 右兄弟穷{InsertBTnode(p, parent->key[i], brother->child[0]);Remove(parent, parent->key[i]);Merge(p, brother); // 注意这个时候p在左边，brother在右边p = p->parent;parent = p->parent;}}else // 如果没有直接相邻的左右兄弟，啥也不管了，直接把父亲拽下来，然后迭代父亲{InsertBTnode(p, parent->key[i], nullptr);//没有左右兄弟，所以为nullptrRemove(parent, parent->key[i]); // 这样是合理的，因为 parent->child[i] 为空p = p->parent;parent = p->parent;}//TraverseBTree();}// 如果变成了根节点，根据定义，根至少有两个孩子，但可以keynum可以少于key_minif (parent == nullptr && p->keynum == 0) // 如果根节点keynum为零了，找一个孩子替代它{root=(root->child[0]==nullptr)?root->child[1]:root->child[0];root->parent=nullptr;delete p;}}void Remove(BTnode *&p, node &x) // 删除函数，给出节点指针和数值，别管这个数值在哪里，不然很麻烦，交给这个函数处理{int i = findpos(p, x);for (int j = i; j <= p->keynum; ++j)p->key[j] = p->key[j + 1],p->child[j] = p->child[j + 1];--p->keynum;}void SuccessOr(Result &res) // 找到后继，替代，并且删除本身{// 注意是引用int &i = res.i;BTnode *&p = res.ptr;if (p->child[i - 1] != nullptr) // 有直接左孩子{BTnode *pre = p->child[i - 1];while (pre->child[pre->keynum] != nullptr)pre = pre->child[pre->keynum];p->key[i] = pre->key[p->keynum];p = pre;i = p->keynum;Remove(p, p->key[i]);}else if (p->child[i] != nullptr) // 有直接右孩子{BTnode *next = p->child[i];while (p->child[0] != nullptr)p = p->child[0];p->key[i] = next->key[1];p = next;i = 1;Remove(p, p->key[i]);}else if (i > 1) // 有直接左兄弟{p->child[i - 1] = p->child[i];Remove(p, p->key[i]);}else if (i < p->keynum) // 有直接右兄弟 为什么这里少一句话，可以思考一下。{Remove(p, p->key[i]);}// else// //在本层及以下没有前驱后继，也就是说这个节点只剩下一个了，// //删除这个节点之后应该直接释放这个节点，但实际上这个情况不可能出现（m大于4时）所以不管它了// {//     Remove(p, p->key[i]);// }}void erase(BTnode *&root, node key, Result &res){SuccessOr(res);// BTnode *p = res.ptr;Adjust(res.ptr);// if (p->parent != nullptr && p->keynum < key_min)// {//     Adjust(p); // 调整// }// else if (p->parent == nullptr && p->keynum == 0)//如果出现了这种情况，不应该这样处理，应该想Adjust那样处理// {//     delete root;//     root = nullptr;// }}

其中，第一个erase函数为public，其他全部为private。

1.看最后的erase函数，它实现了什么功能：调用SuccessOr函数，然后Adjust函数，（其实参数中的key压根没有用到，因为result已经给了所需要的信息。）

2.来看SuccessOr函数，它的功能：在以删除节点为根的树下，找删除节点的直接前驱和直接后继。再来看实现，先明确i是什么，i是删除节点在 key数组的位置。

策略：先找直接前驱，没有直接前驱，找直接后继，先看有没有直接左孩子，有的话就和AVL树一样找叶子哪里的直接前驱，没有的话有左兄弟就直接删除本身，随便把节点改一下（至于为什么只有这里需要改，可以考虑一下。）右边是一样的策略。

也就是说，这个删除就是删除了节点同时移动指针，不管之后会发生什么，有问题就让Adjust来调整树型就好了。

3.全篇最难：调整树型（我挣扎了很长时间。）

循环条件：不为根且节点个数足够。（注意，如果是根的话，即使个数小于key_min也是可以的。）

策略：

1.有左兄弟，且左兄弟富裕。则把父亲插入当前节点，同时把父亲节点赋值成brother的最右节点，最后删除brother最右节点，注意：插入节点的时候要把brother最右儿子给带过去，之后直接break已经不再需要迭代。 思考一下：为什么要有swap，但是在另一种情况下却不需要。

2.有左兄弟，且左兄弟穷。把父亲给拿下来（必须，原因是，等会左右孩子要合并，这是父亲中孩子节点少一个，为了保持B-树的性质，必须要把父亲给拿走一个，不然child没法填。）之后是删除节点和合并兄弟，最后迭代父亲。

3.有右兄弟，且右兄弟富裕。方法与1.相同，但是不需要swap（思考为什么）但多了一句brother->child[0]=brother->child[1]，其实这两个不一样的两句话干的事情是类似的，然后直接break。

4.有右兄弟，且右兄弟穷。与2.相同，但注意合并是p在左。

5.没有左右兄弟（这是可能的！），直接找父亲要（注意一定要的是parent->key[i]，而不是相邻的另一个parent->key[i-1]，这是为了方便Remove函数，可以少写一句parent->child[i-1]=parent->child[i]），然后删除父亲中的对应节点。

循环结束之后，判断是否是根节点，如果是根节点并且根节点被删空，则选择他的一个儿子来替代它本人，最后删除这个舍弃的根节点。

这就是Adjust全过程。然后来看各个辅助函数：

1.Remove 给出节点指针和要删除的值，然后删除同时移动child指针，不要在函数接口有i这个东西。！！！同时注意双亲的双向绑定。

2.Merge给出两个节点指针，把right归并到left中，同时释放right，最后把right置成left，方便后面操作。一个问题：为什么right->child[0]没有被归并代码却是正确的？答案：这一点在函数外保证。

代码结束！

其实洛谷的P1177由于排序的缘故，是从前向后进行erase的，不能完美的测试erase，可以自己造几个数据来判断是否erase合理，当然也可以用这里的代码去写洛谷的P3369普通平衡树来测试，但是我太懒了，就没写P3369，只写了P1177来测试再加上自己的一些手写数据。

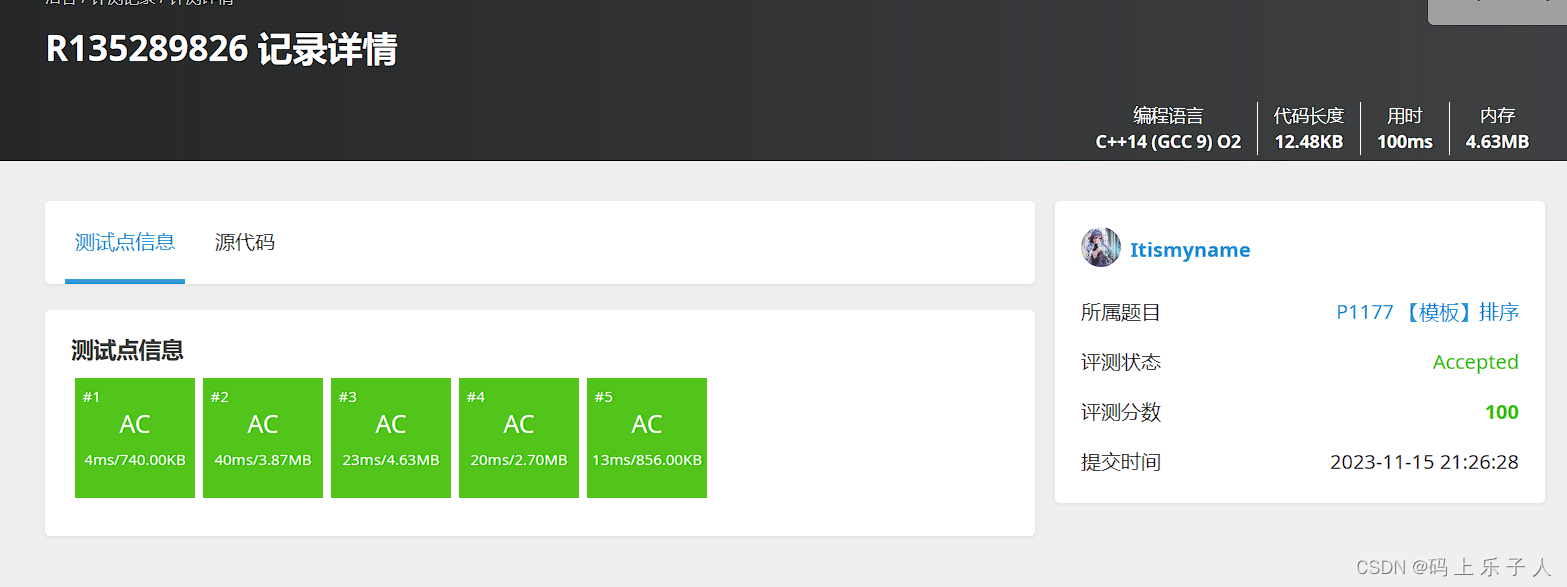
完整代码和AC记录

完整代码（整整500行代码，虽然有部分不是代码。）：

#include <iostream>
#include <cmath>
#include <string>
#include <cstring>
#include <vector>
#include <algorithm>
#include <fstream>#define ll long longusing namespace std;// B-树给我的启示：
// 1.不要在脑子模糊的情况下写算法
// 2.函数的接口要尽可能简单，越方便调用越好
// 3.打持久战要有耐心
// 4.调试函数的存在可能比一个有用的函数更重要
// 5.不要超过两个小时持续思考
// 6.别人的代码可以看，可以借鉴，但是不能全信，
//我看的别人的代码想法很美妙，但是不能细想，一细想发现漏洞百出
// 7.有想法了就去实现
// 8.对拍或者利用oj是个不错的想法
// 9.与AVL树相同，对自己的数据结构制定一个规则，然后通过优雅的方式实现，代码的效率就会极大地提升//吐槽：B-树真的不仅仅是把分块思想用到了排序树吗？
#define m 35struct node
{int key, value;bool operator<(const node &it) const{return key < it.key;}bool operator>(const node &it) const{return key > it.key;}bool operator==(const node &it) const{return key == it.key;}
};struct BTnode
{BTnode *parent = nullptr;int keynum = 0;BTnode *child[m + 1] = {0};node key[m + 1];int Size[m + 1] = {0};
};struct Result
{BTnode *ptr;bool tag;int i;
};class B_Tree
{
private:int Size;BTnode *root;const int key_min = (m - 1) / 2;const int mid = (m + 1) / 2;const int key_max = m - 1;public:B_Tree(){Size = 0;root = nullptr;}bool insert(int x){Result res = search(x);if (res.tag) // 找到了，就个数+1{++res.ptr->key[res.i].value;return false;}else{insert(root, {x, 1}, res);++Size;return true;}}Result search(int x) // 找位置，函数很简单，没啥好说的{BTnode *p = root, *q = nullptr;int i;bool flag = 0;node key = {x, 1};while (p != nullptr && !flag){i = findpos(p, key);if (i <= p->keynum && p->key[i] == key)flag = 1;else{q = p;p = p->child[i - 1];}}if (flag)return {p, flag, i};elsereturn {q, flag, i};}bool erase(int x){Result res = search(x);if (res.tag){if (--res.ptr->key[res.i].value == 0)erase(root, {x, 1}, res);return true;}elsereturn false;}/* 计算出整棵树上记录条数的总和 */int CountKeyNum(BTnode *tree){// 空树则为 0if (tree == NULL)return 0;// 计算所有子树记录条数总和int childTotal = 0;for (int i = 0; i <= tree->keynum; i++){childTotal += CountKeyNum(tree->child[i]);}// 子树加上自身的记录条数，即为总记录条数return tree->keynum + childTotal;}/* 打印 B 树 */void TraverseBTree(BTnode *tree = nullptr){ // 看的别人代码直接复制粘贴的调试函数// 动态创建一个数组，用于存放当前结点是否为最后结点的标识tree = this->root;int nowNum = 0;int *isLast = (int *)malloc(sizeof(int) * (CountKeyNum(tree) + 10));// 打印树形printf("\n");PrintBTree(tree, isLast, nowNum);}/* 递归打印树形 */void PrintBTree(BTnode *tree, int isLast[], int nowNum){// 空树直接跳过if (tree == nullptr)return;// 打印新节点先打印一下平台printf("-|\n");for (int i = 0; i <= tree->keynum; i++){if (tree->child[i] != NULL){printBranch(isLast, nowNum);printf("|----");isLast[nowNum++] = (i == tree->keynum);PrintBTree(tree->child[i], isLast, nowNum);nowNum--;}if (i != tree->keynum){printBranch(isLast, nowNum);printf("|- %d\n", tree->key[i + 1].key);}}}/* 打印树枝 */void printBranch(int isLast[], int nowNum){for (int i = 0; i < nowNum; i++){if (isLast[i])printf(" ");elseprintf("|");printf("      ");}}private:void Merge(BTnode *&left, BTnode *&right) // 把右边归并到左边，并删除右边的节点{for (int i = left->keynum + 1, j = 1; j <= right->keynum; ++j, ++i){left->key[i] = right->key[j];left->child[i] = right->child[j];if (left->child[i] != nullptr) // 把孩子更改父亲left->child[i]->parent = left;++left->keynum;}delete right;right = left;}void Adjust(BTnode *&p) // 调整树型{BTnode *parent = p->parent, *brother;int i;while (p->keynum < key_min && parent != nullptr) // 如果节点个数比较少，同时不为根节点{i = findpos(parent, p->key[1]); // 父亲的编号 当前在 child[i-1] 中if (i > 1 && (brother = parent->child[i - 2]) != nullptr) // 左兄弟不为空， 当前在 child[i-1] 那么 child[i-2]就是左兄弟了{if (brother->keynum > key_min) // 左兄弟富裕{InsertBTnode(p, parent->key[i - 1], brother->child[brother->keynum]); // 把父亲的节点要下来，注意把左兄弟最右端的指针也拿下来swap(p->child[0], p->child[1]);brother->child[brother->keynum] = nullptr;// 这里不需要像有兄弟一样把 child[brother->keynum] 置空，因为减1了，画个图就明白了parent->key[i - 1] = brother->key[brother->keynum]; // 然后父亲替换成左兄弟的最大值Remove(brother, brother->key[brother->keynum]);     // 左兄弟删除这个节点，break;                                              // 调整完成，break}else // 左兄弟穷{InsertBTnode(brother, parent->key[i - 1], p->child[0]); // 把父亲要下来，这个时候父亲那个节点要被删除，把兄弟最右端指针拿下来p->child[0] = nullptr;Remove(parent, parent->key[i - 1]); // 删除父亲Merge(brother, p);                  // 合并兄弟p = p->parent; // 父亲可能节点变少，继续循环parent = p->parent;}}else if (i <= parent->keynum && (brother = parent->child[i]) != nullptr) // 有右兄弟{if (brother->keynum > key_min) // 右兄弟富裕{InsertBTnode(p, parent->key[i], brother->child[0]);brother->child[0] = brother->child[1]; // 这一句别忘了多加，因为右兄弟最左端节点被我拿走了，所以附带的他也为空parent->key[i] = brother->key[1];Remove(brother, brother->key[1]);break;}else // 右兄弟穷{InsertBTnode(p, parent->key[i], brother->child[0]);Remove(parent, parent->key[i]);Merge(p, brother); // 注意这个时候p在左边，brother在右边p = p->parent;parent = p->parent;}}else // 如果没有直接相邻的左右兄弟，啥也不管了，直接把父亲拽下来，然后迭代父亲{InsertBTnode(p, parent->key[i], nullptr); // 没有左右兄弟，所以为nullptrRemove(parent, parent->key[i]);           // 这样是合理的，因为 parent->child[i] 为空p = p->parent;parent = p->parent;}// TraverseBTree();}// 如果变成了根节点，根据定义，根至少有两个孩子，但可以keynum可以少于key_minif (parent == nullptr && p->keynum == 0) // 如果根节点keynum为零了，找一个孩子替代它{root = (root->child[0] == nullptr) ? root->child[1] : root->child[0];root->parent = nullptr;delete p;}}void Remove(BTnode *&p, node &x) // 删除函数，给出节点指针和数值，别管这个数值在哪里，不然很麻烦，交给这个函数处理{int i = findpos(p, x);for (int j = i; j <= p->keynum; ++j)p->key[j] = p->key[j + 1],p->child[j] = p->child[j + 1];--p->keynum;}void SuccessOr(Result &res) // 找到后继，替代，并且删除本身{// 注意是引用int &i = res.i;BTnode *&p = res.ptr;if (p->child[i - 1] != nullptr) // 有直接左孩子{BTnode *pre = p->child[i - 1];while (pre->child[pre->keynum] != nullptr)pre = pre->child[pre->keynum];p->key[i] = pre->key[p->keynum];p = pre;i = p->keynum;Remove(p, p->key[i]);}else if (p->child[i] != nullptr) // 有直接右孩子{BTnode *next = p->child[i];while (p->child[0] != nullptr)p = p->child[0];p->key[i] = next->key[1];p = next;i = 1;Remove(p, p->key[i]);}else if (i > 1) // 有直接左兄弟{p->child[i - 1] = p->child[i];Remove(p, p->key[i]);}else if (i < p->keynum) // 有直接右兄弟{Remove(p, p->key[i]);}// else// //在本层及以下没有前驱后继，也就是说这个节点只剩下一个了，// //删除这个节点之后应该直接释放这个节点，但实际上这个情况不可能出现（m大于4时）所以不管它了// {//     Remove(p, p->key[i]);// }}void erase(BTnode *&root, node key, Result &res){SuccessOr(res);// BTnode *p = res.ptr;Adjust(res.ptr);// if (p->parent != nullptr && p->keynum < key_min)// {//     Adjust(p); // 调整// }// else if (p->parent == nullptr && p->keynum == 0)//如果出现了这种情况，不应该这样处理，应该想Adjust那样处理// {//     delete root;//     root = nullptr;// }}void newroot(BTnode *&root, BTnode *&child1, BTnode *&child2, node &key) // 如果根节点出现了分裂或者初始为空,需要新建一个节点{root = new BTnode;root->keynum = 1;root->key[1] = key;root->child[0] = child1;root->child[1] = child2;root->parent = nullptr;if (child1 != nullptr)child1->parent = root;if (child2 != nullptr)child2->parent = root;return;}void split(BTnode *&p, BTnode *&ap) // p分裂，并分给ap{ap = new BTnode;ap->child[0] = p->child[mid]; // 别忘了for (int i = mid + 1, j = 1; i <= p->keynum; ++i, ++j)ap->key[j] = p->key[i],ap->child[j] = p->child[i];ap->parent = p->parent;ap->keynum = p->keynum - mid;p->keynum = mid - 1;// 双亲和孩子的双向绑定for (int i = 0; i <= ap->keynum; ++i)if (ap->child[i] != nullptr)ap->child[i]->parent = ap;return;}void InsertBTnode(BTnode *&p, node &key, BTnode *ap) // 给出节点，值和指针，不要给出i！！！不然会变得不幸！{int i = findpos(p, key); // i在这里现场获得！！！for (int j = p->keynum; j >= i; --j)p->key[j + 1] = p->key[j],p->child[j + 1] = p->child[j];p->child[i] = ap;p->key[i] = key;p->keynum++;if (ap != nullptr)ap->parent = p;return;}void insert(BTnode *&root, node key, Result &res) // 插入{BTnode *ap = nullptr, *p = res.ptr;bool finished = false;// int i = res.i;//这个i其实屁用没有，因为我坚持i一定要现场获得，不然会变得不幸！while (p != nullptr && !finished){InsertBTnode(p, key, ap);if (p->keynum <= key_max)finished = 1;else{split(p, ap);key = p->key[mid];if (p->parent != nullptr){p = p->parent;// i = findpos(p, key);//不要管i}elsebreak;}}if (!finished) // 如果p是根，说明要么根分裂了，要么树为空newroot(root, p, ap, key);}int findpos(BTnode *&q, node &x) // 作用：找这个节点中第一个大于等于x的下标，PS；永远不可能为0{return lower_bound(q->key + 1, q->key + 1 + q->keynum, x) - q->key;}
};int main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);// fstream p;// p.open("E:\\DOWNLOAD\\P1177_4.in");B_Tree it;int n;cin >> n;int a[n + 1];for (int i = 1; i <= n; ++i){cin >> a[i];it.insert(a[i]);}sort(a + 1, a + 1 + n);// reverse(a+1,a+1+n);for (int i = 1; i <= n; ++i){Result res = it.search(a[i]);if (res.tag)cout << res.ptr->key[res.i].key << ' ';// it.erase(a[i]);}cout << endl;system("pause");return 0;
}

给大伙看一下痛苦的时候的代码：

#include <iostream>
#include <algorithm>
#include <cmath>
#include <fstream>#define ll long long
#define m 35using namespace std;//只实现了insert函数，erase函数没有成功实现。/*
为什么B-树文件索引（磁盘）更优？
1.对磁盘进行访问等同于指针的移动
2.磁盘具有局部访问优化，页访问
3.节点与节点之间，数据是不连续的，可能在不同的页之间
4.B-树比较矮，指针操作较少在把磁盘里的数据加载到内存中的时候，是以页为单位来加载的，
而我们也知道，节点与节点之间的数据是不连续的，所以不同的节点，很有可能分布在不同的磁盘页中
*/struct node{int key,value;bool operator<(const node&it)const{return key<it.key;}bool operator>(const node&it)const{return key>it.key;}bool operator==(const node&it)const{return key==it.key;}
};struct BTNode{int keynum;BTNode*parent;node key[m+1]={0};//0号元素未用BTNode*ptr[m+1]={0};//子树元素指针，0号元素要用！
};  struct result{//tag表示是否找到对于节点int i;//i表示位置bool tag;BTNode*ptr;//指向位置
};//在调整的过程中，牢记一个问题：双亲和孩子的双向绑定（这是在踩了很多坑后总结出来的）class B_Tree{
private:int Size;const int s=(m+1)/2;//中间分裂的位置const int min_key=(m-1)/2;//最小的keynumBTNode*root;
public:B_Tree(){Size=0;root=nullptr;}bool erase(int x){result res=search(x);if(res.tag){if(--res.ptr->key[res.i].value==0)erase(root,{x,0},res);return true;}elsereturn false;}result search(int x){node key={x,0};BTNode*p=root,*q=nullptr;bool flag=0;int i=0;while(p!=nullptr&&!flag){//i最小是1,找的是第一个大于等于key的位置，如果没有，则应该指向p->keynum+1，//即尾指针才对，永远不会在查找时出现0i=lower_bound(p->key+1,p->key+p->keynum+1,key)-p->key;if(i<=p->keynum&&p->key[i]==key)flag=1;else{q=p;p=p->ptr[i-1];//要减去1，这才是应该下一步寻找的位置，书上的太不对啊//因为i指向的是第一个大于等于key的值，但是已知不相等，//所以应该减去1才不会漏过}}if(flag)//返回查找位置{return {i,flag,p};}else//返回插入位置，应该注意的是，如果查找失败，一定返回的是最底层的位置{return {i,flag,q};//返回的是插入节点}}bool insert(int x)//B-tree的插入总是插入到底端节点{result res=search(x);if(res.tag){++res.ptr->key[res.i].value;return false;}elsereturn _insert(root,{x,1},res.ptr,res.i);//最底层的地方，并且i不等于0}/* 计算出整棵树上记录条数的总和 */
int CountKeyNum(BTNode* tree) {// 空树则为 0if (tree == NULL) return 0;// 计算所有子树记录条数总和int childTotal = 0;for (int i = 0; i <= tree->keynum; i++) {childTotal += CountKeyNum(tree->ptr[i]);}// 子树加上自身的记录条数，即为总记录条数return tree->keynum + childTotal;
}/* 打印 B 树 */
void TraverseBTree(BTNode *tree=nullptr) {//看的别人代码直接复制粘贴的调试函数// 动态创建一个数组，用于存放当前结点是否为最后结点的标识tree=this->root;int nowNum = 0;int* isLast = (int*)malloc(sizeof(int) * (CountKeyNum(tree) + 10));// 打印树形printf("\n");PrintBTree(tree, isLast, nowNum);
}/* 递归打印树形 */
void PrintBTree(BTNode *tree, int isLast[], int nowNum) {// 空树直接跳过if (tree == nullptr) return;// 打印新节点先打印一下平台printf("-|\n");for (int i = 0; i <= tree->keynum; i++) {if (tree->ptr[i] != NULL) {printBranch(isLast, nowNum);printf("|----");isLast[nowNum++] = (i == tree->keynum);PrintBTree(tree->ptr[i], isLast, nowNum);nowNum--;}if (i != tree->keynum) {printBranch(isLast, nowNum);printf("|- %d\n", tree->key[i+1].key);}}
}/* 打印树枝 */
void printBranch(int isLast[], int nowNum) {for (int i = 0; i < nowNum; i++) {if (isLast[i]) printf(" ");else printf("|");printf("      ");}
}private:void deleteroot(BTNode*&root)//空根只有一个孩子{//  this->root=root->ptr[0];//  this->root->parent=nullptr;//  delete root;// return ;if(root->ptr[0]!=nullptr){ BTNode*child=root->ptr[0];root->ptr[0]=child->ptr[0];if(child->ptr[0]!=nullptr)child->ptr[0]->parent=root;for(int i=1;i<=child->keynum;++i)_Insert(root,child->key[i],i,child->ptr[i]);delete child;}else{BTNode*child=root->ptr[1];root->ptr[1]=child->ptr[0];if(child->ptr[0]!=nullptr)child->ptr[0]->parent=root;int t=root->keynum;for(int i=1;i<=child->keynum;++i)_Insert(root,child->key[i],i+t,child->ptr[i]);delete child;}}//把右节点合并到左节点中void Combine(BTNode*&left,BTNode*&right){if(left==nullptr)return;//把右节点的信息依次插入左边的最右边for(int i=1;i<=right->keynum;++i){_Insert(left,right->key[i],left->keynum+1,right->ptr[i]);}delete right;right=nullptr;}void Restore(BTNode*&p,int pi){BTNode*parent,*brother;parent=p->parent;while(1){if(pi>0&&(brother=parent->ptr[pi-1])!=nullptr&&brother->keynum>min_key){_Insert(p,parent->key[pi],1,p->ptr[0]);//把左兄弟的父节点给它p->ptr[0]=brother->ptr[brother->keynum];//把最左边的孩子节点改为左兄弟最右边孩子if(brother->ptr[brother->keynum]!=nullptr)//修改左兄弟的最右孩子的父亲brother->ptr[brother->keynum]->parent=p;/*下面的这三步其实是复杂化了，只需要移动几次指针其实就好了*/Remove(parent,pi);//把父亲节点删去，但是不修改指针Insert(parent,pi,brother->key[brother->keynum]);//把左兄弟的最右节点给它，Remove(brother,brother->keynum);//删除最右边的break;}else if(pi<parent->keynum&&(brother=parent->ptr[pi+1])!=nullptr&&brother->keynum>min_key){//和左兄弟同理，也有些复杂化了_Insert(p,parent->key[pi+1],p->keynum+1,brother->ptr[0]);Remove(parent,pi+1);Insert(parent,pi+1,brother->key[1]);Remove(brother,1);for(int i=0;i<=brother->keynum;++i)brother->ptr[i]=brother->ptr[i+1];break;}else if(pi>0&&(brother=parent->ptr[pi-1])!=nullptr)//左兄弟也比较穷即 min_key = (m-1)/2 ，这是两个节点相加不超过m，所以合并！{  _Insert(p,parent->key[pi],1,p->ptr[0]);//把父亲节点拿到当前节点上Remove(parent,pi);//父亲这里删除Combine(brother,p);//兄弟合并p=brother;for(int i=pi;i<=parent->keynum;++i)//父亲这里修改指针parent->ptr[i]=parent->ptr[i+1];if(parent->keynum<min_key)//如果父亲也变穷了{if(parent->parent==nullptr){deleteroot(parent);break;}else{int i=lower_bound(parent->parent->key+1,parent->parent->key+parent->parent->keynum+1,p->key[1])-parent->parent->key-1;p=parent;pi=i;parent=p->parent;//别忘了修改父亲}}else //节点个数正常，直接break;break;}else if(pi<p->keynum&&(brother=parent->ptr[pi+1])!=nullptr){_Insert(p,parent->key[pi+1],p->keynum+1,brother->ptr[0]);Remove(parent,pi+1);Combine(p,brother);for(int i=pi+1;i<=parent->keynum;++i)parent->ptr[i]=parent->ptr[i+1];if(parent->keynum<min_key){if(parent->parent==nullptr){deleteroot(parent);break;}else{int i=lower_bound(parent->parent->key+1,parent->parent->key+parent->parent->keynum+1,p->key[p->keynum+1])-parent->parent->key-1;pi=i;p=parent;parent=p->parent;//parent别忘了修改}}else    //如果父亲节点个数正常，直接breakbreak;  }else{_Insert(p,parent->key[pi],1,p->ptr[0]);Remove(parent,pi);for(int i=pi+1;i<=parent->keynum;++i)parent->ptr[i]=parent->ptr[i+1];if(parent->keynum<min_key){if(parent->parent==nullptr){deleteroot(parent);break;}else{int i=lower_bound(parent->parent->key+1,parent->parent->key+parent->parent->keynum+1,p->key[p->keynum+1])-parent->parent->key-1;pi=i;p=parent;parent=p->parent;//parent别忘了修改}}else    //如果父亲节点个数正常，直接breakbreak;  }}}void Insert(BTNode*&p,int i,node&x)//把x插入p的第i个位置{if(p==nullptr)return;for(int j=p->keynum;j>=i;--j)p->key[j+1]=p->key[j];p->key[i]=x;++p->keynum;}void Remove(BTNode*&p,int i)//删除这个节点{/*删除记录这一部分，我省略了删除孩子指针的步骤，为什么呢？这里是为了方便后续的树形调整函数如果只删除记录的话，会导致孩子指针比原本多出一个，但好处也很明显，到后边有一个双亲记录替换的需求，我提供了只删除记录和只插入记录的操作，可以在不影响孩子指针的情况下完成记录值的替换*/if(p==nullptr)return;for(;i<p->keynum;++i)//左移p->key[i]=p->key[i+1];p->keynum--;return;}void Successor(BTNode*&p,int &i)//获得前驱节点，并替换i和p{if(p==nullptr)return;//如果是空（比如本来就是最底层）if(p->ptr[i-1]==nullptr)return;BTNode*res=p->ptr[i-1];while(res->ptr[res->keynum]!=nullptr)res=res->ptr[res->keynum];p->key[i]=res->key[res->keynum];p=res;i=res->keynum;}void Next(BTNode*&p,int &i){if(p==nullptr)return;if(p->ptr[i]==nullptr)return;BTNode*res=p->ptr[i];while(res->ptr[0]!=nullptr)res=res->ptr[0];p->key[i]=res->key[1];p=res;i=1;}//问题在于没有前驱怎么办void erase(BTNode*&root,node x,result&res){int flag=0;if(res.ptr->ptr[res.i-1]!=nullptr)//判断当前节点是不是最下层非终端节点Successor(res.ptr,res.i);//不是，则替换else if(res.ptr->ptr[res.i]!=nullptr){    Next(res.ptr,res.i);flag=1;}x=res.ptr->key[res.i];//保存要删除的那个节点，BTNode*parent=res.ptr->parent;//如果是根节点，就不再调整，因为既然删除操作放生在了根节点，说明已经没有了左右兄弟和双亲了//如果不是根节点，并且节点个数比较少，if(parent!=nullptr&&res.ptr->keynum-1<min_key){Remove(res.ptr,res.i);//删除这个节点//在父节点找它的位置，因为已经被remove了，可以预测肯定是找不到这个节点的//这时得到最后一个小于本身的进行restoreint pi=lower_bound(parent->key+1,parent->key+parent->keynum+1,x)-parent->key-1+flag;Restore(res.ptr,pi);/*这里的 RestoreBTree 函数，我和其他地方的不一样，参数 pi 并不是关键字在目标结点中的位置，而是整个目标节点在双亲节点中的位置，这样做的好处上边也提到了，可以很方便地找到左右双亲和左右兄弟也可以注意到 pi = Search -1; 这一句，和上边的 child[i-1] 是一样的道理，都是找到双亲中孩子的位置*/}else{for(int i=res.i;i<res.ptr->keynum;++i){res.ptr->key[i]=res.ptr->key[i+1];res.ptr->ptr[i]=res.ptr->ptr[i+1];}--res.ptr->keynum;}return;}void split(BTNode*&q,const int &mid,BTNode*&ap)//节点q的mid之后全部分给ap，但是mid之前全部保留{int i,j;ap=new BTNode;ap->ptr[0]=q->ptr[mid];//节点零是这个时候会去填写的for(i=mid+1,j=1;i<=m;++i,++j)//优化的话，可以考虑这里改成move函数{ap->key[j]=q->key[i];ap->ptr[j]=q->ptr[i];}ap->keynum=m-mid;ap->parent=q->parent;//置于同一层，保证最底层在同一层次上，就这么一句话保证了在插入时所有最下端节点都在同一层上for(i=0;i<=m-mid;++i)if(ap->ptr[i]!=nullptr)ap->ptr[i]->parent=ap;q->keynum=mid-1;//后面的全部舍弃}void _Insert(BTNode*&q,node&x,int i,BTNode*&ap){for(int j=q->keynum;j>=i;--j){q->key[j+1]=q->key[j];q->ptr[j+1]=q->ptr[j];}q->key[i]=x;q->ptr[i]=ap;if(ap!=nullptr){ap->parent=q;}++q->keynum;}void newroot(BTNode*&T,BTNode*&p,node&x,BTNode*&ap)//这个函数只对根节点使用！{T=new BTNode;T->keynum=1;T->ptr[0]=p;T->ptr[1]=ap;T->key[1]=x;if(p!=nullptr)p->parent=T;if(ap!=nullptr)ap->parent=T;T->parent=nullptr;}bool _insert(BTNode*&T,node x,BTNode*q,int i){bool finished=false;BTNode*ap=nullptr;//ap表示x所在的节点的指针，初始时为空，毕竟是节点while(q!=nullptr&&!finished){_Insert(q,x,i,ap);//事实上，i不可能为0if(q->keynum<m)finished=1;else{split(q,s,ap);x=q->key[s];//q=q->parent;//问题出现在了这里，如果q变成了空，那么下面判断出根节点出现了分裂，//那应该是把q放在新的根节点的最左子树上，但是q却变成了空，那还放个屁，直接没有了//就是这里的问题导致的时不时会出错而且不容易发现，超你妈的费我老半天劲找不出来为什么。//这样insert函数就十分完善了，if(q->parent!=nullptr){q=q->parent;i=lower_bound(q->key+1,q->key+q->keynum+1,x)-q->key;}else break;}}//如果根节点为空，或者根节点出现分裂，//因为finished为false，只能是根节点为空或者根节点出现了分裂if(!finished)newroot(T,q,x,ap);return true;}
};int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);fstream p;p.open("E:\\DOWNLOAD\\P1177_1.in");B_Tree it;int n;cin>>n;int a[n+1];for(int i=1;i<=n;++i){cin>>a[i];it.insert(a[i]);// it.TraverseBTree();}sort(a+1,a+1+n);//int tot=unique(a+1,a+1+n)-a-1;for(int i=1;i<=n;++i){it.TraverseBTree();result p=it.search(a[i]);if(p.tag)cout<<a[i]<<' ';it.erase(a[i]);}//it.TraverseBTree();cout<<endl;system("pause");return 0;
}

这一点似乎在名字上也有所体现。

其他平衡树

手搓平衡树：一颗B-树，一颗AVL树，一颗RB树，一颗Splay树，一颗带旋Treap，一颗无旋fhq-Treap，一颗01Trie-CSDN博客