近几年信息学竞赛CSP中常考的排列组合知识点

本文主要是介绍近几年信息学竞赛CSP中常考的排列组合知识点，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

蒟蒻来讲题，还望大家喜。若哪有问题，大家尽可提！

Hello 大家好啊！我们今天讲一下排列组合！！！

===========================================================================================

近几年排列组合的题（本蒟蒻整理的）

排列组合

计数原理

分类计数（加法原理）

分步计数（乘法原理）

例题

排列

线排

捆绑法

插空法

定序

环排

项链

组合

特殊元素

分组问题

分组分配

总结

===========================================================================================

首先给大家看一下近几年排列组合的题（本蒟蒻整理的）：

2008年普及组

书架上有 4本不同的书 A、B、C、D。其中 A 和 B 是红皮的，C 和 D 是黑皮的。把这 4本书摆在书架上，满足所有黑皮的书都排在一起的摆法有_____种。满足 A 必须比 C 靠左，所有红皮的书要摆放在一起，所有黑皮的书要摆放在一起，共有______种摆法。

2010年普及组

队列快照是指在某一时刻队列中的元素组成的有序序列。例如，当元素 1,2,3入队，元素 1出队后，此刻的队列快照是2,3。当元素2,3 也出队后，队列快照是""，即为空。现有3 个正整数元素依次入队、出队。已知它们的和为 8，则共有_________种可能的不同的队列快照（不同队列的相同快照只计一次）。例如，"5,1"、"4,2,2"、""都是可能的队列快照；而"7"不是可能的队列快照，因为剩下的 2 个正整数的和不可能是 1。

2012年普及组

在 NOI 期间，主办单位为了欢迎来自各国的选手，举行了盛大的晚宴。在第十八桌，有 5名大陆选手和 5名港澳选手共同进膳。为了增进交流，他们决定相隔就坐，即每个大陆选手左右旁都是港澳选手，每个港澳选手左右旁都是大陆选手。那么，这一桌一共有_______种不同的就坐方案。

注：如果在两个方案中，每个选手左右相邻的选手相同，则视为同一种方案。

2013年普及组

7 个同学围坐一圈，要选 2个不相邻的作为代表，有_________ 种不同的选法。

2014年普及组

把 M个同样的球放到 N个同样的袋子里，允许有的袋子空着不放问共有多少种不同的放置方法？(用 K 表示)。

例如，M=7,N=3 时，K=8；在这里认为 (5,1,1) 和 (1,5,1)是同一种放置方法。问：M=8,N=5时，K=______

2015年普及组

重新排列1234 使得每一个数字都不在原来的位置上，一共有 __种排法。

2016年普及组

从一个 4×4 的棋盘（不可旋转）中选取不在同一行也不在同一列上的两个方格，共有_______种方法。
有7个一模一样的苹果，放到3个一样的盘子中，一共有（）种放法。

2017年普及组

甲、乙、丙三位同学选修课程，从 4 门课程中，甲选修 2 门，乙、丙各选修3门，则不同的选修方案共有（）种。

2018年普及组

从1到2018这2018个数中，共有__________个包含数字8 的数。

2019年普及组

1. 把8个同样的球放在5个同样的袋子里，允许有的袋子空着不放，问共有多少种不同的分法？

提示：如果8个球都放在一个袋子里，无论是哪个袋子，都只算同一种分法。

2. —些数字可以颠倒过来看，例如0,1,8颠倒过来还是本身，6颠倒过来是9，9颠倒过来看还是6，其他数字颠倒过来都不构成数字。类似的，一些多位数也可以颠倒过来看，比如106颠倒过来是901。假设某个城市的车牌只由5位数字组成，每一位都可以取0到9。请问这个城市最多有多少个车牌倒过来恰好还是原来的车牌？（）

2020年普及组

1. 5 个小朋友并排站成一列，其中有两个小朋友是双胞胎，如果要求这两个双胞胎必须相邻，则有（）种不同排列方法?

2. 10 个三好学生名额分配到7个班级，每个班级至少有一个名额，一共有（）种不同的分配方案。

3. 有五副不同颜色的手套（共10只手套，每副手套左右手各 1只），一次性从中取6只手套，请问恰好能配成两副手套的不同取法有（）种。

2021年普及组

1. 6 个人，两个人组一队，总共组成三队，不区分队伍的编号。不同的组队情况有（）种。

2. 由1,1,2,2,3这五个数字组成不同的三位数有（）种。

大家不难发现，近几年排列组合的题越来越多，所以今日本蒟蒻来讲一讲！

排列组合

计数原理

计数原理主要分两个板块分类计数（加法原理）和分步计数（乘法原理）！

分类计数（加法原理）

加法原理，顾名思义，就是相加呗！而只有当一个问题需要分类求解时，才会用加法原理！

分步计数（乘法原理）

乘法原理，顾名思义，就是相乘呗！而只有当一个问题需要分步求解时，才会用乘法原理！

理论说完了，不懂的话，那就看例题吧！

例题

例1：0,1,2,3,4,5这五个数字组成一个三位数，有多少个？。

想必有些人是这么做的： $C_{5}^{1}\times C_{5}^{1}\times C_{4}^{1}$

这样就是第一位不能为0，所以就是5个里选1个，然后第二位还剩5个数，最后第三位填时只剩4个数，所以是四

个里选一个！

看似很对，但其实是错的！

为什么呢？因为题目中三位数并没有说数字不能重复，就比如说211，这也是三位数！而刚才算的是每一位不重

复的三位数！

所以应该是这样的： $C_{5}^{1}\times C_{6}^{1}\times C_{6}^{1}$

所以我们在做题的时候一定要注意细节，这道题就是典型的也是最简单的一到乘法原理的题！

例2: 0,1,2,3,4,5组成一个不同不重复的三位偶数，有多少种组法？

我想有一部分人会这么做： $C_{5}^{1}\times C_{5}^{1}\times C_{3}^{1}$

这样就是最后有三种可能0,2,4，而第一位就是去了0，就剩5个数，第二位再加上0，还是5个数可以选。

感觉可以，实则不对

最后一位如果不是0的话那你前面第一位还是 $C_{5}^{1}$ 吗？

所以，我们这时候就要用到分类了！

当0在末尾时： $C_{5}^{1}\times C_{4}^{1}$ （就是第一位可以选1,2,3,4,5,第二位可以选第一位选完剩下的）

当0不在末尾是： $C_{4}^{1}\times C_{4}^{1}\times C_{2}^{1}$ （最后一位只能选2或4，第一位则只可以选剩下的4个，第二位也是四个因为

加上了0）

最终答案就是： $C_{5}^{1}\times C_{4}^{1} +C_{4}^{1}\times C_{4}^{1}\times C_{2}^{1}$

这就是一道既有乘法原理的题，又有加法原理的题！

排列

排列就主要分为线排，错排，圆排，项链排。

线排

线排主要就是按行排列！

例题1：7个人排队，甲不站在队首。

这道题显然是很简单的： $C_{6}^{1}\times A_{6}^{6}$

甲不站在队首有6种可能，然后剩下的人全排列就行了！

例题2：7个人排队，甲不站在队首，乙不站在队尾。

这道题就要想一想了！

如果甲加站在队尾，那么乙便有6种选择，然后剩下的人全排列。

如果甲不站在队尾，那么甲有5种选择，乙也有5种选择，然后剩下的人全排列。

所以这道题就是： $C_{6}^{1}\times A_{5}^{5}+C_{5}^{1}\times C_{5}^{1}\times A_{5}^{5}$

捆绑法

顾名思义，就是把几个人捆一块，那什么时候用呢？当求谁和谁相邻的问题时！

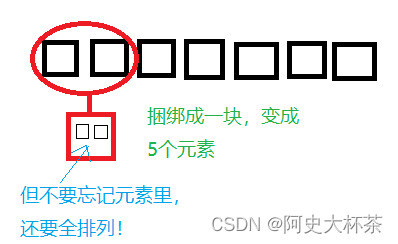
例题：7个人排队，甲乙丙相邻，有几种排法？

这就用到捆绑法了！

把甲乙丙3人看成1人，然后进行全排列，别忘了！甲乙丙三人也需要全排列！

所以这道题就是： $A_{5}^{5}\times A_{3}^{3}$

插空法

插空法就是解决不相邻的时候用，下面几个例题说明！

例题：7个人排队，甲乙不相邻，有几种排法？

我们用图来表示：

我们可以发现有6个空位可以选，这样就可以使甲乙不相邻，但不要忘记甲和乙可以互换！所以是： $A_{6}^{2}$

所以最终是： $A_{6}^{2}\times A_{5}^{5}$

定序

定序就是按一定的顺序排列。

例题：七个人排队，甲比乙位置靠前，乙比丙位置靠前，问有几种排列方法？

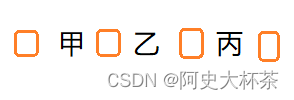
这个题我们就可以用插空法，我们知道甲乙丙位置是可以固定的，所以我们要给剩下的人插进去。但是大家一

定要注意：插完一个人之后会再多一个空！

看到了没有？所以本题应是： $C_{4}^{1}\times C_{5}^{1}\times C_{6}^{1}\times C_{7}^{1}$

环排

环排就是围成一个圆来坐。

例题：6个人排成一个圆，有几种排列方式？

大家可能觉得是： $A_{6}^{6}$

但肯定不是的，要不不就和线排一样了么？

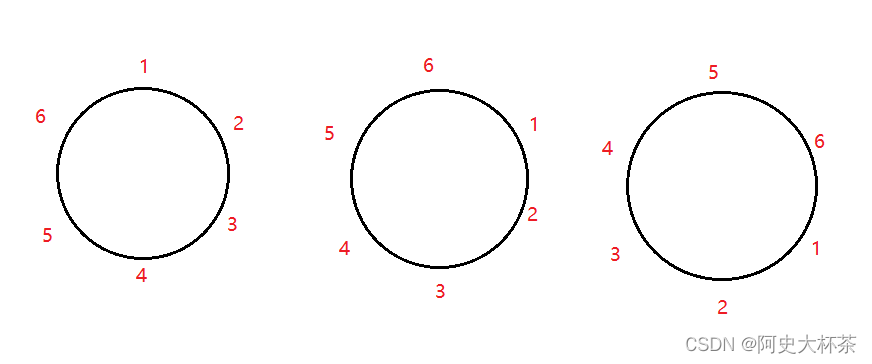
大家请看，这几个做法是不是一样的，但是 $A_{6}^{6}$ 中却多算了6个1的位置，所以我们要除以六，大家也可以认为是

让1的位置不变，然后就是 $A_{5}^{5}$ ！

项链

项链就是可以翻转，你想一想你带项链的时候是不是正着戴和反着戴一个样？

所以我们就在环排的基础上再除以2就行了！

组合

特殊元素

特殊元素问题相信大家一看例题就懂了！

例题：一个班有30个人，选四人参加参加比赛，甲必须参加。

相信这个题对大家来说已经不是困难了！

答案就是： $C_{29}^{3}$

像这样的题，就是特殊元素问题！

分组问题

例题1:7本不同的数，分成4本，2本，1本三堆，有几种分法？

这道题也是相当的简单了： $C_{7}^{4}\times C_{3}^{2}\times C_{1}^{1}$

例题2：6本不同的数，分成2本，2本，2本三堆，有几种分法？

这道题就有一点意思了！

有些人可能会说： $C_{6}^{2}\times C_{4}^{2}\times C_{2}^{2}$

但其实根本就不是这样！

大家可以想一下，你和我分组，我分第一组，你分第二组和我分第二组，你分第一组，光算组合其实是一

样的！

这道题我们就要平均分了，要除以多少呢，就是重复的全排列。

所以就是： $\frac{C_{6}^{2}\times C_{4}^{2}\times C_{2}^{2}}{A_{3}^{3}}$

分组分配

分组分配最重要的就是：先分组，再分配！

例题：4个人分到3个工厂，每个工厂至少1人，有多少种分法？

这道题就是先分给3个工厂，这里就只能一个2人其余的1人。

所以，我们先选出来 $C_{4}^{2}\times C_{2}^{1}\times C_{1}^{1}$ ，然后就完事了么？不不不！别忘了平均分在除以 $A_{2}^{2}$ ，还得乘 $A_{3}^{3}$ 让这

几个人进行排序！

最终就是： $\frac{C_{4}^{2}\times C_{2}^{1}\times C_{1}^{1}}{A_{2}^{2}}\times A_{3}^{3}$

总结

最后我们用球盒问题来总结一下！

1. 球不同，盒不同 $\rightarrow$ 这就是我们的分组分配问题！

2. 球相同，盒不同 $\rightarrow$ 这就用我们学的隔板法！

3. 球不同，盒相同 $\rightarrow$ 这就是纯分组问题！

4. 球相同，盒相同 $\rightarrow$ 这就是我们的分类加法！

今天的排列组合就到这里了，喜欢的点个赞谢谢！

这篇关于近几年信息学竞赛CSP中常考的排列组合知识点的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

近几年信息学竞赛CSP中常考的排列组合知识点

首先给大家看一下近几年排列组合的题（本蒟蒻整理的）：

排列组合

计数原理

分类计数（加法原理）

分步计数（乘法原理）

例题

排列

线排

捆绑法

插空法

定序

环排

项链

组合

特殊元素

分组问题

分组分配

总结

相关文章

基本知识点

两个月冲刺软考——访问位与修改位的题型(淘汰哪一页)；内聚的类型；关于码制的知识点；地址映射的相关内容

CSP 2023 提高级第一轮 CSP-S 2023初试题完善程序第二题解析未完

每日一题|牛客竞赛|四舍五入|字符串+贪心+模拟

生信代码入门：从零开始掌握生物信息学编程技能

STL经典案例（四）——实验室预约综合管理系统（项目涉及知识点很全面，内容有点多，耐心看完会有收获的！）

生信圆桌x生信分析平台：助力生物信息学研究的综合工具

C++语法知识点合集：11.模板

枚举相关知识点

【408数据结构】散列（哈希）知识点集合复习考点题目