跟着我学Python进阶篇：01.试用Python完成一些简单问题

2023-12-20 21:52
文章标签 python 简单 问题 进阶篇 完成 01 跟着 试用 我学

本文主要是介绍跟着我学Python进阶篇：01.试用Python完成一些简单问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

往期文章

跟着我学Python基础篇：01.初露端倪
跟着我学Python基础篇：02.数字与字符串编程
跟着我学Python基础篇：03.选择结构
跟着我学Python基础篇：04.循环
跟着我学Python基础篇：05.函数
跟着我学Python基础篇：06.列表
跟着我学Python基础篇：07.文本
跟着我学Python基础篇：08.集合和字典

目录

  • 往期文章
  • 前言
  • 1. 图形：简单绘图
    • 1.1 创建窗口
    • 1.2 线和多边形
  • 2. 使用Sympy进行符号处理
    • 2.1 操作表达式
      • 2.1.1化简表达式
      • 2.1.2 展开表达式
      • 2.1.3 因式分解表达式
      • 2.1.4 求导数
      • 2.1.5 求积分
    • 2.2 求解方程
      • 2.2.1 求解一元方程
      • 2.2.2求解多元方程
      • 2.2.3 求解高阶多项方程
      • 2.2.4 求解三角方程
      • 2.2.5 求解指数方程
    • 2.3 画函数图像
  • 3. 随机数的生成和模拟
    • 3.1 模拟掷骰子
    • 3.2 模拟打靶
    • 3.3 生成随机密码

前言

在基础篇，我们已经掌握了Python中的一些基础的语法规则，那么在进阶篇中，我们将在更深度一些的层次上，去学习和了解Python。

1. 图形：简单绘图

matplotlib是一个用于创建高质量图形的Python库。它可以用于绘制各种类型的图形，包括线图、散点图、条形图、直方图、饼图等。matplotlib提供了丰富的图形定制选项，允许用户自定义各种元素，如标签、标题、轴标签、颜色、线型等。此外，matplotlib还可以与numpy、pandas等其他Python库一起使用，以便更轻松地处理和可视化数据。

1.1 创建窗口

import matplotlib.pyplot as plt# 创建一个图形窗口
fig = plt.figure()# 可选：设置窗口的大小和标题
fig.set_size_inches(6, 4)  # 设置窗口大小为6x4英寸
fig.suptitle('My Window')  # 设置窗口标题# 显示窗口
plt.show()

在这里插入图片描述
我们首先使用plt.figure()创建了一个图形窗口对象fig。然后，我们可以使用fig.set_size_inches()和fig.suptitle()来设置窗口的大小和标题。

1.2 线和多边形

import matplotlib.pyplot as plt# 创建一个图形窗口
fig = plt.figure()# 可选：设置窗口的大小和标题
fig.set_size_inches(6, 4)  # 设置窗口大小为6x4英寸
fig.suptitle('My Window')  # 设置窗口标题# 绘制折线图
x = [1, 2, 3, 4, 5]
y = [5, 4, 3, 2, 1]
plt.plot(x, y)# 显示窗口
plt.show()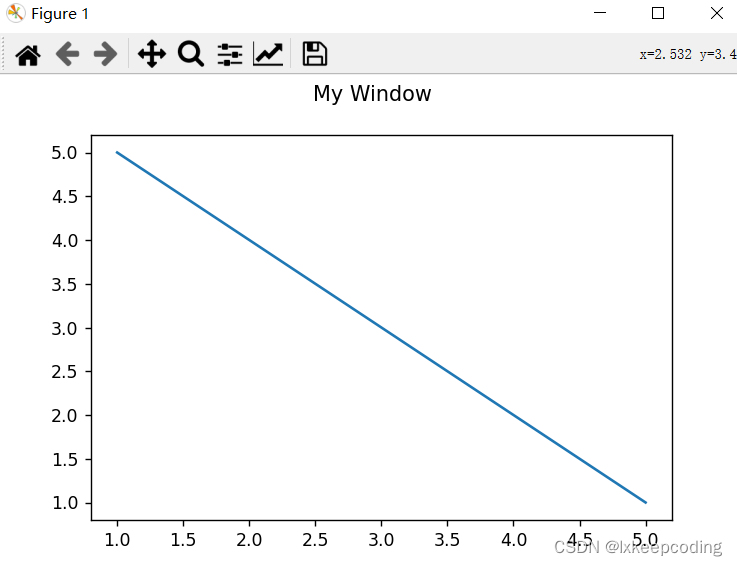

在这里插入图片描述
我们首先创建了一个图形窗口，并设置了窗口的大小和标题。然后使用plt.plot()函数绘制了一个折线图，最后使用plt.show()函数显示图形窗口。你可以根据需要在窗口中绘制不同类型的图形。

import matplotlib.pyplot as plt# 数据
x = ['A', 'B', 'C', 'D']
y = [10, 15, 7, 12]# 创建一个图形窗口
fig = plt.figure()# 绘制柱状图
plt.bar(x, y)# 显示图形
plt.show()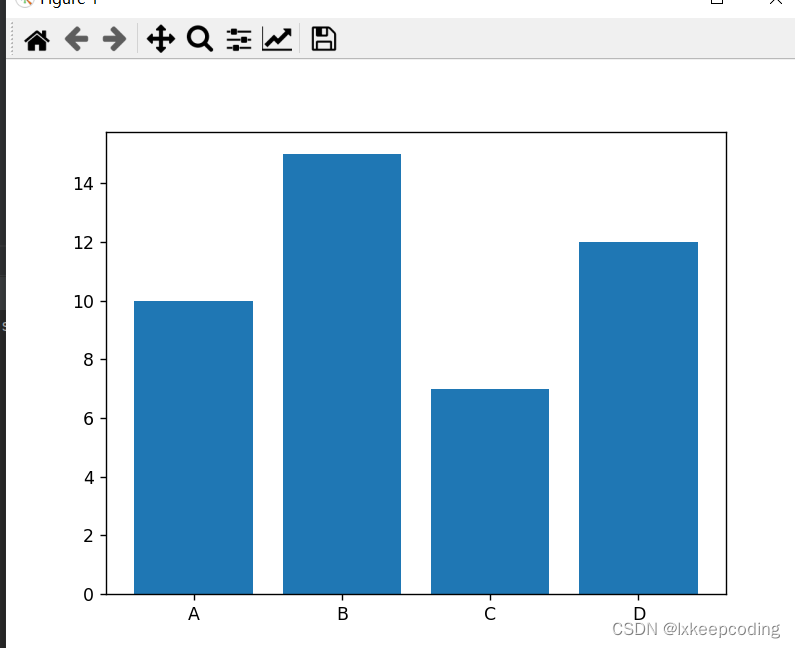

在这里插入图片描述
我们定义了两个列表x和y，分别表示柱状图的横轴和纵轴数据。然后创建一个图形窗口，使用plt.bar()函数绘制柱状图。最后使用plt.show()函数显示图形窗口。

import matplotlib.pyplot as plt# 数据
x = ['A', 'B', 'C', 'D']
y = [10, 15, 7, 12]# 颜色
colors = ['red', 'green', 'blue', 'orange']# 创建一个图形窗口
fig = plt.figure()# 绘制柱状图并填充颜色
plt.bar(x, y, color=colors)# 显示图形
plt.show()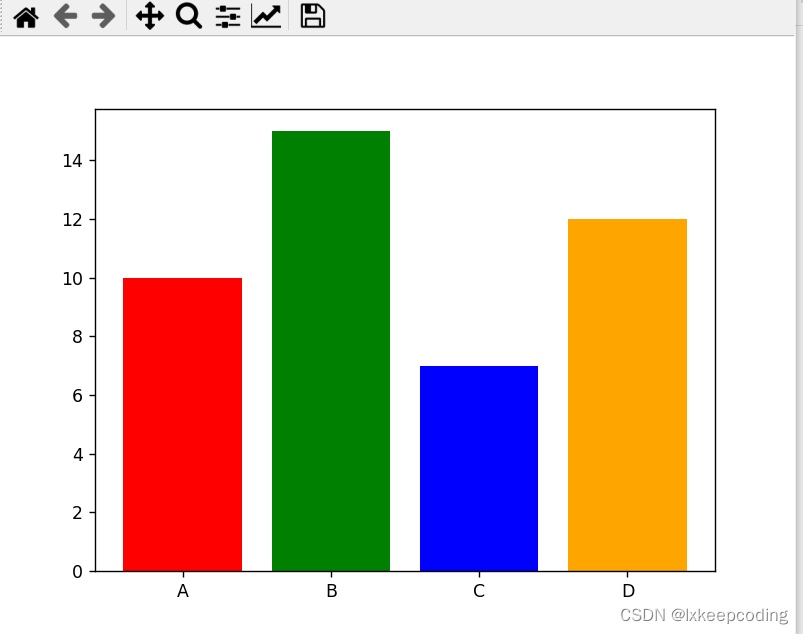

在这里插入图片描述
定义了一个colors列表，其中每个元素对应柱状图中每个柱子的颜色。然后创建一个图形窗口，使用plt.bar()函数绘制柱状图，并通过color参数指定填充颜色。最后使用plt.show()函数显示图形窗口。你可以根据实际需求调整x、y和colors的值，以及使用其他参数来自定义柱状图的样式，如宽度、边框颜色等。

2. 使用Sympy进行符号处理

sympy包提供了大量的函数可以计算更多公式的值，包括微积分。让我们来感受一下。

2.1 操作表达式

2.1.1化简表达式

`Sympy可以将表达式自动化简为最简形式。以下是一个例子：

import sympy# 定义符号变量x和y
x, y = sympy.symbols('x y')# 定义表达式
expr = 2*x + x - x**2# 化简表达式
simplified_expr = sympy.simplify(expr)# 输出化简后的表达式
print(simplified_expr)

在这里插入图片描述

在这个例子中，我们定义了一个表达式2*x + x - x**2，使用sympy.simplify()函数将其化简为最简形式，并将结果存储在变量simplified_expr中。最后，我们使用print()函数输出化简后的表达式。

2.1.2 展开表达式

Sympy可以将表达式展开为多项式。以下是一个例子：

import sympy# 定义符号变量x和y
x, y = sympy.symbols('x y')# 定义表达式
expr = (x + y)**2# 展开表达式
expanded_expr = sympy.expand(expr)# 输出展开后的表达式
print(expanded_expr)

在这里插入图片描述

在这个例子中，我们定义了一个表达式(x + y)**2，使用sympy.expand()函数将其展开为多项式，并将结果存储在变量expanded_expr中。最后，我们使用print()函数输出展开后的表达式。

2.1.3 因式分解表达式

将表达式因式分解为乘积形式。以下是一个例子：

import sympy# 定义符号变量x和y
x, y = sympy.symbols('x y')# 定义表达式
expr = x**2 - y**2# 因式分解表达式
factored_expr = sympy.factor(expr)# 输出因式分解后的表达式
print(factored_expr)

在这里插入图片描述

在这个例子中，我们定义了一个表达式x2 - y2，使用sympy.factor()函数将其因式分解为x + y)*(x - y)的乘积形式，并将结果存储在变量actored_expr中。最后，我们使用print()函数输出因式分解后的表达式。

2.1.4 求导数

Sympy可以对表达式求导数。以下是一个例子：

import sympy# 定义符号变量x和y
x, y = sympy.symbols('x y')# 定义表达式
expr = x**3 + 2*x**2 + x# 对表达式求导
derivative_expr = sympy.diff(expr, x)# 输出求导后的表达式
print(derivative_expr)

在这里插入图片描述

在这个例子中，我们定义了一个表达式x3 + 2*x2 + x，使用sympy.diff()函数对其求导，并将结果存储在变量derivative_expr中。最后，我们使用print()函数输出求导后的表达式。

2.1.5 求积分

import sympy# 定义符号变量x和y
x, y = sympy.symbols('x y')# 定义表达式
expr = x**3 + 2*x**2 + x# 对表达式求积分
integral_expr = sympy.integrate(expr, x)# 输出求积分后的表达式
print(integral_expr)

在这里插入图片描述

在这个例子中，我们定义了一个表达式x3 + 2*x2 + x，使用sympy.integrate()函数对其求积分，并将结果存储在变量integral_expr中。最后，我们使用print()函数输出求积分后的表达式。

2.2 求解方程

2.2.1 求解一元方程

import sympy# 定义符号变量x
x = sympy.symbols('x')# 定义方程
equation = sympy.Eq(x**2 - 4, 0)# 求解方程
solutions = sympy.solve(equation, x)# 输出方程的解
print(solutions)

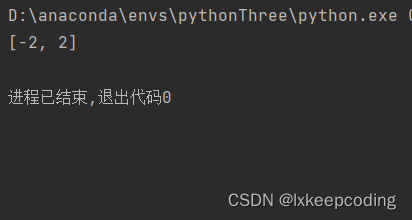
在这里插入图片描述
我们定义了一个一元方程x**2 - 4 = 0，使用sympy.solve()函数来求解方程，并将结果存储在变量solutions中。最后，我们使用print()函数输出方程的解。

2.2.2求解多元方程

import sympy# 定义符号变量x和y
x, y = sympy.symbols('x y')# 定义方程组
equations = [sympy.Eq(x + y, 5),sympy.Eq(2*x - y, 1)
]# 求解方程组
solutions = sympy.solve(equations, (x, y))# 输出方程组的解
print(solutions)

在这里插入图片描述
我们定义了一个多元方程组，包含两个方程x + y = 5和2*x - y = 1。我们使用sympy.solve()函数来求解方程组，并将结果存储在变量solutions中。最后，我们使用print()函数输出方程组的解。

2.2.3 求解高阶多项方程

import sympy# 定义符号变量x
x = sympy.symbols('x')# 定义高阶多项式方程
equation = x**4 - 6*x**3 + 11*x**2 - 6*x# 求解方程
solutions = sympy.solve(equation, x)# 输出方程的解
print(solutions)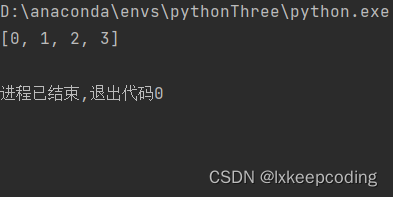

在这里插入图片描述
高阶多项式方程x4 - 6*x3 + 11x**2 - 6x，使用sympy.solve()函数求解方程，并将结果存储在变量solutions中。最后，我们使用print()函数输出方程的解。

2.2.4 求解三角方程

import sympy# 定义符号变量x
x = sympy.symbols('x')# 定义三角方程
equation = sympy.sin(x) - sympy.cos(x)# 求解方程
solutions = sympy.solve(equation, x)# 输出方程的解
print(solutions)

在这里插入图片描述
我们定义了一个三角方程sin(x) - cos(x)，使用sympy.solve()函数求解方程，并将结果存储在变量solutions中。最后，我们使用print()函数输出方程的解。

2.2.5 求解指数方程

import sympy# 定义符号变量x
x = sympy.symbols('x')# 定义指数方程
equation = sympy.exp(x) - 2**x# 求解方程
solutions = sympy.solve(equation, x)# 输出方程的解
print(solutions)

在这里插入图片描述

2.3 画函数图像

import sympy
from sympy.plotting import plot# 定义符号变量x
x = sympy.symbols('x')# 定义函数
f = x**2# 绘制函数图像
p = plot(f, (x, -5, 5), show=False)# 设置标题和坐标轴标签
p.title = 'Function Graph'
p.xlabel = 'x'
p.ylabel = 'y'# 显示图像
p.show()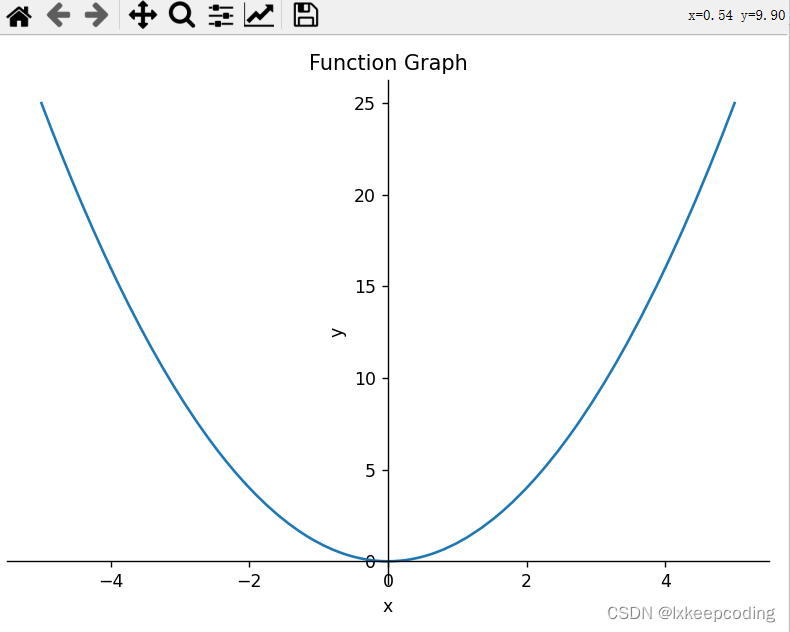

在这里插入图片描述
我们定义了一个函数f(x) = x**2，使用sympy库的plot()函数来绘制函数的图像。第一个参数是要绘制的函数，第二个参数是函数自变量的范围。plot()函数还有许多其他参数可以用来定制图像，例如线条颜色、线条样式等。
最后，我们设置了标题和坐标轴标签，并使用show()函数显示图像。
注意，sympy库的绘图功能相对于专业的绘图库可能较为简单，因此对于绘制复杂的图像，建议使用更专业的绘图库，例如matplotlib。

3. 随机数的生成和模拟

3.1 模拟掷骰子

import pygame
import sys
import random
import timepygame.init()WINDOW_SIZE = (400, 400)
screen = pygame.display.set_mode(WINDOW_SIZE)
pygame.display.set_caption("Rolling Dice Animation")DICE_POINTS = {1: [(200, 200)],2: [(170, 170), (230, 230)],3: [(170, 170), (200, 200), (230, 230)],4: [(170, 170), (230, 230), (170, 230), (230, 170)],5: [(170, 170), (230, 230), (170, 230), (230, 170), (200, 200)],6: [(170, 170), (230, 230), (170, 230), (230, 170), (170, 200), (230, 200)],
}def draw_dice(number):screen.fill((255, 255, 255))pygame.draw.rect(screen, (0, 0, 0), (150, 150, 100, 100))for point in DICE_POINTS[number]:pygame.draw.circle(screen, (255, 0, 0), point, 10)pygame.display.flip()def roll_dice_animation():current_number = 1for _ in range(30):draw_dice(current_number)current_number = random.randint(1, 6)time.sleep(0.1)return current_numberdef main():while True:for event in pygame.event.get():if event.type == pygame.QUIT:pygame.quit()sys.exit()result = roll_dice_animation()print(f"Dice rolled: {result}")time.sleep(1)  # 停留一秒，显示掷出的点数if __name__ == "__main__":main()

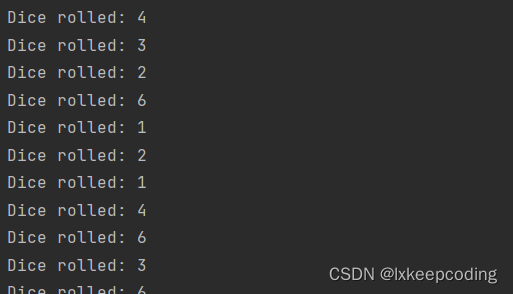
在这里插入图片描述
在这里插入图片描述

3.2 模拟打靶

import pygame
import sys
import randompygame.init()WINDOW_SIZE = (400, 400)
screen = pygame.display.set_mode(WINDOW_SIZE)
pygame.display.set_caption("Target Shooting Simulation")TARGET_RADIUS = 50  # 调整靶子半径
TARGET_COLOR = (255, 0, 0)
BACKGROUND_COLOR = (255, 255, 255)shots = []def draw_target():pygame.draw.circle(screen, TARGET_COLOR, (200, 200), TARGET_RADIUS)def draw_shots():for shot in shots:pygame.draw.circle(screen, (0, 255, 0), shot[0], 5)font = pygame.font.Font(None, 36)text = font.render(str(shot[1]), True, (0, 255, 0))screen.blit(text, (shot[0][0] - 10, shot[0][1] - 20))def calculate_score(distance):max_distance = TARGET_RADIUSmin_distance = 0normalized_distance = max(0, min((max_distance - distance) / max_distance, 1))score = int(normalized_distance * 10)return scoredef main():clock = pygame.time.Clock()while True:for event in pygame.event.get():if event.type == pygame.QUIT:pygame.quit()sys.exit()elif event.type == pygame.MOUSEBUTTONDOWN and event.button == 1:  # 左键点击mouse_x, mouse_y = pygame.mouse.get_pos()distance = ((mouse_x - 200) ** 2 + (mouse_y - 200) ** 2) ** 0.5if distance <= TARGET_RADIUS:score = calculate_score(distance)print(f"Hit! Score: {score}")shots.append(((mouse_x, mouse_y), score))screen.fill(BACKGROUND_COLOR)draw_target()draw_shots()pygame.display.flip()clock.tick(60)if __name__ == "__main__":main()

在这里插入图片描述

3.3 生成随机密码

import random
import stringdef generate_password(length=12):characters = string.ascii_letters + string.digits + string.punctuationpassword = ''.join(random.choice(characters) for _ in range(length))return password# 生成一个默认长度为12的密码
password = generate_password()
print("Generated Password:", password)

在这里插入图片描述

这篇关于跟着我学Python进阶篇：01.试用Python完成一些简单问题的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/517632。

相关文章

Python中的魔术方法__new__详解

Python中的魔术方法__new__详解

《Python中的魔术方法__new__详解》：本文主要介绍Python中的魔术方法__new__的使用,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录一、核心意义与机制1.1 构造过程原理1.2 与 __init__ 对比二、核心功能解析2.1 核心能力2.2
阅读更多...
Python虚拟环境终极(含PyCharm的使用教程)

Python虚拟环境终极(含PyCharm的使用教程)

《Python虚拟环境终极(含PyCharm的使用教程)》：本文主要介绍Python虚拟环境终极(含PyCharm的使用教程),具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,... 目录一、为什么需要虚拟环境？二、虚拟环境创建方式对比三、命令行创建虚拟环境（venv）3.1 基础命令3
阅读更多...
Python Transformer 库安装配置及使用方法

Python Transformer 库安装配置及使用方法

《PythonTransformer库安装配置及使用方法》HuggingFaceTransformers是自然语言处理（NLP）领域最流行的开源库之一,支持基于Transformer架构的预训练模... 目录python 中的 Transformer 库及使用方法一、库的概述二、安装与配置三、基础使用：Pi
阅读更多...
Python 中的 with open文件操作的最佳实践

Python 中的 with open文件操作的最佳实践

《Python中的withopen文件操作的最佳实践》在Python中,withopen()提供了一个简洁而安全的方式来处理文件操作,它不仅能确保文件在操作完成后自动关闭,还能处理文件操作中的异... 目录什么是 with open()？为什么使用 with open()？使用 with open() 进行
阅读更多...
Python中使用正则表达式精准匹配IP地址的案例

Python中使用正则表达式精准匹配IP地址的案例

《Python中使用正则表达式精准匹配IP地址的案例》Python的正则表达式(re模块)是完成这个任务的利器,但你知道怎么写才能准确匹配各种合法的IP地址吗,今天我们就来详细探讨这个问题,感兴趣的朋... 目录为什么需要IP正则表达式？IP地址的基本结构基础正则表达式写法精确匹配0-255的数字验证IP地
阅读更多...
MySQL 中查询 VARCHAR 类型 JSON 数据的问题记录

MySQL 中查询 VARCHAR 类型 JSON 数据的问题记录

《MySQL中查询VARCHAR类型JSON数据的问题记录》在数据库设计中,有时我们会将JSON数据存储在VARCHAR或TEXT类型字段中,本文将详细介绍如何在MySQL中有效查询存储为V... 目录一、问题背景二、mysql jsON 函数2.1 常用 JSON 函数三、查询示例3.1 基本查询3.2
阅读更多...
使用Python实现全能手机虚拟键盘的示例代码

使用Python实现全能手机虚拟键盘的示例代码

《使用Python实现全能手机虚拟键盘的示例代码》在数字化办公时代,你是否遇到过这样的场景：会议室投影电脑突然键盘失灵、躺在沙发上想远程控制书房电脑、或者需要给长辈远程协助操作？今天我要分享的Pyth... 目录一、项目概述：不止于键盘的远程控制方案1.1 创新价值1.2 技术栈全景二、需求实现步骤一、需求
阅读更多...
Python 迭代器和生成器概念及场景分析

Python 迭代器和生成器概念及场景分析

《Python迭代器和生成器概念及场景分析》yield是Python中实现惰性计算和协程的核心工具,结合send()、throw()、close()等方法,能够构建高效、灵活的数据流和控制流模型,这... 目录迭代器的介绍自定义迭代器省略的迭代器生产器的介绍yield的普通用法yield的高级用法yidle
阅读更多...
使用Python将JSON,XML和YAML数据写入Excel文件

使用Python将JSON,XML和YAML数据写入Excel文件

《使用Python将JSON,XML和YAML数据写入Excel文件》JSON、XML和YAML作为主流结构化数据格式,因其层次化表达能力和跨平台兼容性,已成为系统间数据交换的通用载体,本文将介绍如何... 目录如何使用python写入数据到Excel工作表用Python导入jsON数据到Excel工作表用
阅读更多...
Pyserial设置缓冲区大小失败的问题解决

Pyserial设置缓冲区大小失败的问题解决

《Pyserial设置缓冲区大小失败的问题解决》本文主要介绍了Pyserial设置缓冲区大小失败的问题解决,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面... 目录问题描述原因分析解决方案问题描述使用set_buffer_size()设置缓冲区大小后，buf
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2