fisher判别分析原理及实现

本文主要是介绍fisher判别分析原理及实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

参考资料：

周志华老师的《机器学习》
http://wiki.mbalib.com/wiki/%E5%88%A4%E5%88%AB%E5%88%86%E6%9E%90

判别分析是一种经典的现行分析方法，其利用已知类别的样本建立判别模型，对未知类别的样本进行分类。在这里我们主要讨论fisher判别分析的方法。

fishter原理

费歇（FISHER）判别思想是投影，使多维问题简化为一维问题来处理。选择一个适当的投影轴,使所有的样品点都投影到这个轴上得到一个投影值。对这个投影轴的方向的要求是：使每一类内的投影值所形成的类内离差尽可能小，而不同类间的投影值所形成的类间离差尽可能大。

公式推导

这里给出一个二维的示意图（摘自周志华老师的《机器学习》一书），在接下来的讨论中我们也将以二维的情况做分类来逐步分析原理和实现。
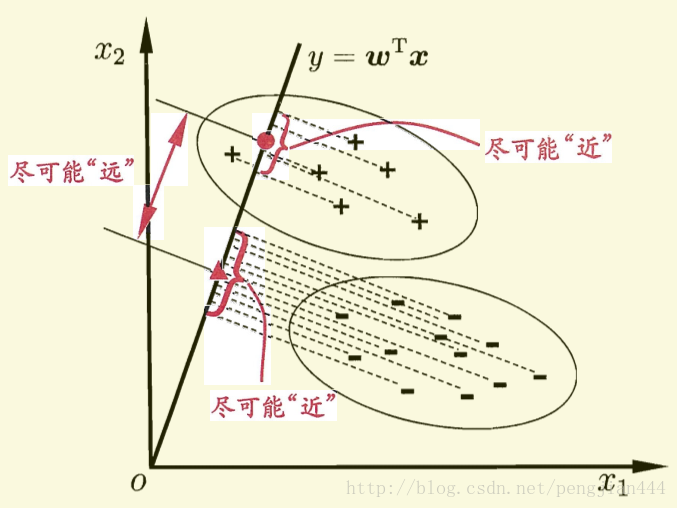
摘自周志华老师的机器学习
ps: 图中有一处描述似乎不是特别的准确，直线的方程应该是

0=wTx

而不是

y=wTx

ps: 因为在书关于此的其他讨论中，并未涉及任何y的概念，这里将y写入对我造成了某种误导。

对于给定的数据集，D（已经设置好分类标签），

Xi,Ui,∑i
分别表示给定类别

i
上，则样本中心的投影为

0=w1∗u1+w2∗u2+⋯+wn∗un
。(n 为样本维度，接下来的讨论中将统一设置为2)，写成向量形式则为

wTu=0
如果将所有的样本都投影到直线上，则两类样本的协方差分别为

wT∑0w和wT∑1w
。要想达到较好的分类效果，应该是的同类样本的投影点尽可能的接近，也就是让同类样本投影点的协方差尽可能的小。即

(wT∑0w+wT∑0w)
尽可能小。同时也应该保证不同类样本投影点尽可能的互相远离，即

∥∥wTu0−wTu1∥∥
尽可能大。如果同时考虑两者的关系可以得到下面需要最大化的目标：

J=∥∥wTu0−wTu1∥∥wT∑0w+wT∑0w

这里定义“类内散度矩阵”（within-class scatter matrix）

Sw=∑0+∑1=∑x∈X0(x−u0)(x−u0)T+∑x∈X1(x−u1)(x−u1)T

以及类间离散度矩阵（between-class scatter matrix）

Sb=(u0−u1)(u0−u1)T

则

ps:sorry 这些公式确实敲得有点累，道个歉，我直接截图了。希望不影响大家的理解。

这里写图片描述

在推导出上面的公式之后我们就可以开始写代码了。

编程实现

数据生成

这里我偷一个懒，直接用scikit-learn的接口来生成数据：

from sklearn.datasets import make_multilabel_classification
import numpy as np

x, y = make_multilabel_classification(n_samples=20, n_features=2,
n_labels=1, n_classes=1,
random_state=2) # 设置随机数种子，保证每次产生相同的数据。

# 根据类别分个类
index1 = np.array([index for (index, value) in enumerate(y) if value == 0]) # 获取类别1的indexs
index2 = np.array([index for (index, value) in enumerate(y) if value == 1]) # 获取类别2的indexs

c_1 = x[index1] # 类别1的所有数据(x1, x2) in X_1
c_2 = x[index2] # 类别2的所有数据(x1, x2) in X_2

fisher算法实现


def cal_cov_and_avg(samples):"""给定一个类别的数据，计算协方差矩阵和平均向量:param samples: :return: """u1 = np.mean(samples, axis=0)cov_m = np.zeros((samples.shape[1], samples.shape[1]))for s in samples:t = s - u1cov_m += t * t.reshape(2, 1)return cov_m, u1

def fisher(c_1, c_2):
“”"
fisher算法实现(请参考上面推导出来的公式，那个才是精华部分)
:param c_1:
:param c_2:
:return:
“”"
cov_1, u1 = cal_cov_and_avg(c_1)
cov_2, u2 = cal_cov_and_avg(c_2)
s_w = cov_1 + cov_2
u, s, v = np.linalg.svd(s_w) # 奇异值分解
s_w_inv = np.dot(np.dot(v.T, np.linalg.inv(np.diag(s))), u.T)
return np.dot(s_w_inv, u1 - u2)

判定类别

def judge(sample, w, c_1, c_2):"""true 属于1false 属于2:param sample::param w::param center_1::param center_2::return:"""u1 = np.mean(c_1, axis=0)u2 = np.mean(c_2, axis=0)center_1 = np.dot(w.T, u1)center_2 = np.dot(w.T, u2)pos = np.dot(w.T, sample)return abs(pos - center_1) < abs(pos - center_2)

w = fisher(c_1, c_2) # 调用函数，得到参数w
out = judge(c_1[1], w, c_1, c_2) # 判断所属的类别
print(out)

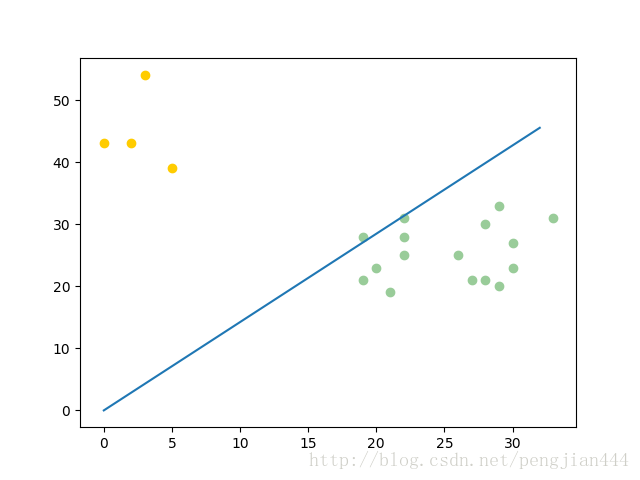
绘图

import matplotlib.pyplot as plt

plt.scatter(c_1[:, 0], c_1[:, 1], c=’#99CC99’)
plt.scatter(c_2[:, 0], c_2[:, 1], c=’#FFCC00’)
line_x = np.arange(min(np.min(c_1[:, 0]), np.min(c_2[:, 0])),
max(np.max(c_1[:, 0]), np.max(c_2[:, 0])),
step=1)