本文主要是介绍C语言课程设计之旅游景点咨询系统,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
C语言课程设计之旅游景点咨询系统
1.问题描述:创建一个至少有15个点的有向网表示的某个旅游景点的导游图。顶点代表景点,类型为字符串(例如,泰山导游图:“天地广场门”,“十八盘”,“冯玉祥墓”,“桃花峪门”,“中天门”,“南天门”,“玉皇顶”等),弧表示两个景点之间可以直达,弧上的权值表示两个景点之间的路程(公里数),弧上还有到达方法的信息(有步行和索道两种)。建立一个游客咨询系统。
2.基本要求
(1)创建图的存储结构。
(2)输入两个景点名,就可以得到从一个景点到达另一个景点的所有简单路径、相应路径的路程公里数、行走的方法(每一段是步行,还是坐索道);
(3)输入两个景点名,就可以得到其最短路径,即:路程最短的行进方法;如果两者无路径可通,就得出“两景点不可达的信息”。
(4)按照题意要求独立进行设计,设计结束后按要求写出设计报告。
一、代码块:
#include<bits/stdc++.h>
/*#include<iostream>
#include<fstream>
#include<algorithm>
#include<stack>*/
using namespace std;
const int MAXVEX=50;
const int INF=0x3fffffff;
//s表示索道 w表示步行typedef struct{//边的结构int wei;//权值char way;//到达方式
}EdgeType;typedef struct{string vexs[MAXVEX];//顶点信息,string类型EdgeType arc[MAXVEX][MAXVEX];//边的信息int numVertexes,numEdges;//顶点数和边数
}MGraph;void CreateMGraph(MGraph *G)
{FILE *fp;fp=fopen("read.txt","r");int i,j,k,w;cout<<"请输入顶点数和边数"<<endl;//cin>>G->numVertexes>>G->numEdges;fscanf(fp,"%d %d",&G->numVertexes,&G->numEdges);cout<<"请输入"<<G->numVertexes<<"个景点名"<<endl;char temp[MAXVEX];for(i=0;i<G->numVertexes;++i){fscanf(fp,"%s",temp);//cin>>G->vexs[i];G->vexs[i]=temp;}//初始化邻接矩阵for(i=0;i<G->numVertexes;++i)for(j=0;j<G->numVertexes;++j)G->arc[i][j].wei=INF;cout<<"请输入"<<G->numEdges<<"条边,包括起点下标、终点下标、路程(KM)和到达方式(s表示索道 w表示步行)"<<endl;for(k=0;k<G->numEdges;++k){char ch;fscanf(fp,"%d %d %d %c",&i,&j,&w,&ch);//cin>>i>>j>>w>>ch;G->arc[i][j].wei=w;G->arc[i][j].way=ch;}cout<<endl<<"*******邻接矩阵建立完成,各景点对应的编号如下*******"<<endl<<endl;for(i=0;i<G->numVertexes;++i){cout<<"编号"<<i<<" "<<G->vexs[i]<<endl;}
}int solution[MAXVEX];//记录路线
bool vis[MAXVEX];//标记数组
int flag;//通路标记void print(MGraph G,int len)//参数为路径上的第几个点
{flag=1;int sum=0;cout<<G.vexs[solution[1]];for(int i=2;i<=len;++i){//第一个点已经打印,打印剩下的点if(G.arc[solution[i-1]][solution[i]].way=='s') cout<<" -> "<<"(索道)"<<G.vexs[solution[i]];else cout<<" -> "<<"(步行)"<<G.vexs[solution[i]];sum+=G.arc[solution[i-1]][solution[i]].wei;}cout<<endl<<"该路径总路程为"<<sum<<"KM"<<endl;cout<<endl;
}void dfs(MGraph G,int k,int loc,int e)//k为第几步,loc为当前的位置,e为目标
{solution[k]=loc;//当前顶点加入路线vis[loc]=1;//标记置为1if(loc==e) print(G,k);elsefor(int i=0;i<G.numVertexes;++i){if(vis[i]==0&&G.arc[loc][i].wei<INF) dfs(G,k+1,i,e);}vis[loc]=0;//取消标记
}void slove_allpath(MGraph G,int s,int e)//查找所有可行路径
{flag=0;//有无路径标记memset(vis,0,sizeof(vis));dfs(G,1,s,e);//从第一步起点开始if(!flag) cout<<"无可行路径!"<<endl;
}int P[MAXVEX][MAXVEX];//用于存储最短路径下标的数组
int D[MAXVEX][MAXVEX];//用于存储到各点最短路径的权值之和void ShortestPath_Dijkstra(MGraph G,int v0)//最短路求解
{int v,w,k,Min;int Final[MAXVEX];//标记,=1表示求得顶点V0至Vw的最短路径for(v=0;v<G.numVertexes;v++){//初始化数据Final[v]=0;//全部顶点初始化为未知最短路径状态D[v0][v]=G.arc[v0][v].wei;//将与V0有连线的顶点加上权值P[v0][v]=v0;//初始化路径数组pre顶点均为起始点V0}D[v0][v0]=0;//v0至v0路径为0Final[v0]=1;//v0至v0不需要求路径for(v=1;v<G.numVertexes;v++){Min=INF;//初始化最小值为INFfor(w=0;w<G.numVertexes;w++){if(!Final[w]&&D[v0][w]<Min){k=w;Min=D[v0][w];//w顶点离v0顶点更近}}Final[k]=1;//将目前找到的最近的顶点位置置为1for(w=0;w<G.numVertexes;++w){//修正当前最短路径及距离//如果经过v顶点的路径比现在这条路径的长度短的话if(!Final[w]&&(Min+G.arc[k][w].wei<D[v0][w])){D[v0][w]=Min+G.arc[k][w].wei;//修改当前路径长度P[v0][w]=k;}}}
}stack<int> xiang;//辅助栈void slove_ShortestPath(MGraph G,int s,int e)//查找最短路径
{int tempe=e;if(D[s][e]==INF) cout<<"无可行路径!"<<endl;else{//有最短路径int temp=D[s][e];xiang.push(e);//终点先进栈while(P[s][e]!=s)//根据P数组倒着找{//只要不到起点xiang.push(P[s][e]);e=P[s][e];}//cout<<"由"<<G.vexs[s]<<"到"<<G.vexs[tempe]<<"的最短路径为:"<<endl;cout<<G.vexs[s];int pre=s;while(!xiang.empty()){int top=xiang.top();if(G.arc[pre][top].way=='s') cout<<" -> "<<"(索道)"<<G.vexs[top];else cout<<" -> "<<"(步行)"<<G.vexs[top];pre=top;xiang.pop();}cout<<endl<<"该路径总路程为"<<temp<<"KM"<<endl;}cout<<endl;
}int main()
{MGraph G;CreateMGraph(&G);for(int i=0;i<G.numVertexes;++i) ShortestPath_Dijkstra(G,i);/*for(int i=0;i<G.numVertexes;++i){for(int j=0;j<G.numVertexes;++j)cout<<P[i][j]<<' ';cout<<endl;}cout<<endl;for(int i=0;i<G.numVertexes;++i){for(int j=0;j<G.numVertexes;++j)cout<<D[i][j]<<' ';cout<<endl;}*/cout<<"请输入需要查找的路径(对应的起点和终点下标),输入-1结束查找"<<endl;int s,e;while(cin>>s>>e&&(s+e)>=0){if(s==e){cout<<"您已在该景点"<<endl;continue;}cout<<"*******由"<<G.vexs[s]<<"到"<<G.vexs[e]<<"可行的路径有:*******"<<endl;slove_allpath(G,s,e);//查找所有可行路径cout<<"*******由"<<G.vexs[s]<<"到"<<G.vexs[e]<<"的最短路径为:*******"<<endl;slove_ShortestPath(G,s,e);//查找最短路径}cout<<"********************查 找 结 束********************"<<endl;return 0;
}
二、运行:
1.读入景点信息文件:

2.查找:


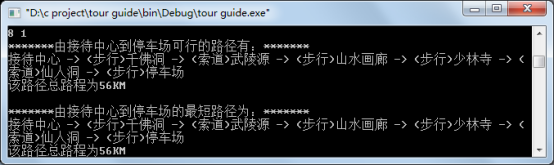
这篇关于C语言课程设计之旅游景点咨询系统的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




