本文主要是介绍leetcode 153. 寻找旋转排序数组中的最小值(优质解法),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

代码:
class Solution {public int findMin(int[] nums) {int left=0,right=nums.length-1;int refer=nums[right];while (left<right){int mid=left+(right-left)/2;if(nums[mid]>refer){left=mid+1;}else {right=mid;}}return nums[left];}
}
题解:
通过题意我们知道,传入的参数是经过旋转的递增数组,如 3,4,5,1,2,就是通过 1,2,3,4,5 旋转得到的,而这种旋转数组的特性我们可以通过一张图清晰的看出来,以 3,4,5,1,2 为例
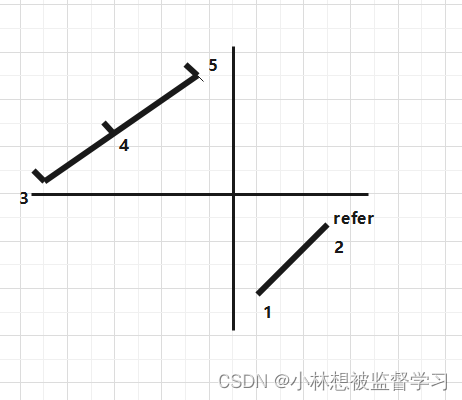
我们可以看出旋转以后的递增数组大多呈现这样的结构,我们将数据分为了两个区间,而需要获取的答案位于下面区间的左边界
我们可以以数组的最后一个数据作为 refer 参照,在数组中选取一个数 nums[ i ],这个数可能会位于上面和下面两个区间
(1).当 nums[ i ] > refer 时,说明该数位于上面的区间,那我们就可以大胆去除掉 i 下标指向的数据以及左边的数据
(2).当 nums[ i ] <= refer 时,说明该数位于下面的区间,那我们就可以大胆去除掉 i 下标右边的数据(但我们不能确定 i 下标指向的是否刚好是我们需要的数据,所以我们不能去除掉 i 下标指向的数据)
通过上面的分析,我们已经能够确定,该题目具有二段性,所以我们可以通过二分法来解决该问题
以 nums = 3,4,5,1,2 为例,用 L 和 R 指针指向数组的两端,mid = left+(right-left)/2= 2 .此时 R 指针指向的刚好是数组的最后一个数据,我们可以顺便记录起来,作为参照值,refer = nums[ R ] = 2
此时 nums[ mid ] = 5 > refer,所以在上面的区间,我们就可以大胆去除 mid 指针以及 mid 指针左边的数据,让 L = mid+1
3 4 5 1 2
L mid R
计算中间值 mid = 3,此时 nums[ mid ] = 1 < refer, 所以在下面的区间,我们就可以大胆去除 mid 右边的数据,让 R =mid
3 4 5 1 2
L R
mid
当 L 和 R 指针相遇时,我们便找到了下面区间的左边界,直接返回 nums[ L ] 即可
3 4 5 1 2
L
R
这篇关于leetcode 153. 寻找旋转排序数组中的最小值(优质解法)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





