爱因斯坦思考题[超详细C++版]

2023-12-15 09:10
文章标签 c++ 详细 爱因斯坦 思考题

本文主要是介绍爱因斯坦思考题[超详细C++版]，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

对二维表中的每个元素进行枚举遍历，依次确定每个表格元素的值，当二维表中所有表格元素的值都确定后，检查其结果是否符合问题解的要求，如果满足要求，则输出一个结果，如果不满足要求，则按照一定的顺序继续遍历各个表格元素的值。这也是一种典型的解空间搜索方式，通过对这个问题的理解，未来遇到类似的问题，或三维表空间的问题，都可以用类似的方法设计搜索算法。

问题介绍

据说是爱因斯坦提出来的，他宣称世界上只有 2％ 的人能解出这个题目，这种说法不一定属实，但是这个推理题还是很有意思的。题目是这样的，据说有五个不同颜色的房间排成一排，每个房间里分别住着一个不同国籍的人，每个人都喝一种特定品牌的饮料，抽一种特定品牌的烟，养一种宠物，没有任意两个人抽相同品牌的香烟，或喝相同品牌的饮料，或养相同的宠物，问题是谁在养鱼作为宠物？为了寻找答案，爱因斯坦给出了 15 条线索：

  • （1）英国人住在红色的房子里
  • （2）瑞典人养狗作为宠物
  • （3）丹麦人喝茶
  • （4）绿房子紧挨着白房子，在白房子的左边
  • （5）绿房子的主人喝咖啡
  • （6）抽 Pall Mall 牌香烟的人养鸟
  • （7）黄色房子里的人抽 Dunhill 牌香烟
  • （8）住在中间那个房子里的人喝牛奶
  • （9）挪威人住在第一个房子里面
  • （10）抽 Blends 牌香烟的人和养猫的人相邻
  • （11）养马的人和抽 Dunhill 牌香烟的人相邻
  • （12）抽 BlueMaster 牌香烟的人喝啤酒
  • （13）德国人抽 Prince 牌香烟
  • （14）挪威人和住在蓝房子的人相邻
  • （15）抽 Blends 牌香烟的人和喝矿泉水的人相邻

问题的状态与数据模型

这个问题和题目给出的 15 条线索一样，都是最终答案的一部分，这个最终答案就是下面表格所展示的内容，知道了谁养鱼，也就能同时知道这个人是德国人，住在绿色房子里，喜欢喝咖啡和抽 Prince 牌子的香烟。通过对问题的理解，这里描述了 5 个人，有不同的国籍，住不同颜色的房子，养不同的宠物，抽不同的香烟，喝不同的饮料，显然这个二维表格描述的整体才是我们要求的解。

房子颜色国籍饮料宠物烟
黄色挪威水猫Dunhill
蓝色丹麦茶马Blends
红色英国牛奶鸟PallMall
绿色德国咖啡鱼Prince
白色瑞典啤酒狗BlueMaster

解空间就是所有这五类元素（房子颜色、国籍、饮料、宠物和烟）的枚举组合，每个组合的结果就是一个状态，状态是上述二维表格的一个实例，每个属性都通过枚举组合确定了，但是还不一定是问题的解，因为判断条件不一定满足。

对状态是不是正确的解的判断也比其他问题复杂，需要用给出的 15 条线索逐条检查组合得到的状态。如果某个状态能够通过 15 条线索的检查，那么就认为找到了一个正确的答案，然后输出该答案。

基本模型定义

这个问题定义的状态二维表共有 25 个属性，这些属性分为 5 个类别，每个类别都有 5 个不同的值可供选择。如果任由这 25 个属性离散存在，会给设计算法带来困难，一般算法建模都会用各种数据结构将这些属性组织起来，仔细观察这些属性，会发现每个属性都可以用“类型+值（TLV）”二元组来描述。用 TLV 描述每个属性的好处是我们不需要将 25 个属性分成 5 类区别处理，在算法穷举的过程中，可以对这 25 个属性进行一致性处理。根据这个原则，我们把属性的数据结构定义如下：

typedef enum 
{type_house = 0,type_nation = 1,type_drink = 2,type_pet = 3,type_cigaret = 4
}ITEM_TYPE;typedef struct
{ITEM_TYPE type;int value;
}ITEM;

我们在介绍算法设计的常用技巧时提到，在设计数据结构和算法时利用数组下标的技巧

const int GROUPS_ITEMS = 5;
typedef struct 
{int itemValue[GROUPS_ITEMS];
}GROUP;
使用这种定义数据结构的方式，不仅可以减少设计算法实现的麻烦，还可以提高算法执行效率。比如现在要查看一个 GROUP 绑定组中房子的颜色是否是蓝色，就可以这样编写代码
if(group.itemValue[type_house] == COLOR_BLUE)
{......
}

线索模型定义

先分析一下这 15 条线索，大致可以分成三类：

  • 第一类是描述某些属性之间具有固定绑定关系的线索，比如，“丹麦人喝茶”和“住绿房子的人喝咖啡”等，线索 1、2、3、5、6、7、12、13 可归为此类；
  • 第二类是描述某些属性类型所在的“组”所具有的相邻关系的线索，比如，“养马的人和抽 Dunhill 牌香烟的人相邻”和“抽 Blends 牌香烟的人和养猫的人相邻”等，线索 10、11、14、15 可归为此类；
  • 第三类就是不能描述属性之间固定关系或关系比较弱的线索，比如，“绿房子紧挨着白房子，在白房子的左边”和“住在中间那个房子里的人喝牛奶”等。

对于第一类具有绑定关系的线索，绑定关系描述中有两组 TLV的信息。以线索3：“丹麦人喝茶”这条绑定线索为例，第一组 TLV 信息是“国籍-丹麦”，第二组 TLV 信息是“饮料类型-茶”。绑定关系的意义在于对于一个 group 关系来说，当其某个属性符合绑定描述的第一组条件时，则其与第二组 TLV信息中指定的类型相同的另一个属性的值也必须与第二组 TLV 中要求的值匹配，否则的话就不符合这个绑定关系。对于绑定类型的线索，其数学模型可以这样定义：

typedef struct
{ITEM_TYPE first_type;int first_value;ITEM_TYPE second_type;int second_value;
}BIND;

有了 BIND 数据结构的定义，线索 1、2、3、5、6、7、12、13 就可以组织起来，存储在一个 binds 数组中：

const BIND binds[] = 
{{ type_house, COLOR_RED, type_nation, NATION_ENGLAND },{ type_nation, NATION_SWEDEND, type_pet, PET_DOG },{ type_nation, NATION_DANMARK, type_drink, DRINK_TEA },{ type_house, COLOR_GREEN, type_drink, DRINK_COFFEE },{ type_cigaret, CIGARET_PALLMALL, type_pet, PET_BIRD },{ type_house, COLOR_YELLOW, type_cigaret, CIGARET_DUNHILL },{ type_cigaret, CIGARET_BLUEMASTER, type_drink, DRINK_BEER },{ type_nation, NATION_GERMANY, type_cigaret, CIGARET_PRINCE }
};

对于第二类描述元素所在的“组”具有相邻关系的线索，相邻关系的描述中也有两组 TLV 的信息。相邻关系和绑定关系的区别在于，绑定关系要检查的两组 TLV 是同一个 group 中的两个属性，而相邻关系要检查的是一个 group 中的一个属性和与这个 group 相邻的另一个 group 中的一个属性之间的关联关系。关联关系的数学模型可以这样定义：

typedef struct
{ITEM_TYPE type;int value;ITEM_TYPE relation_type;int relation_value;
}RELATION;

type 和 value 是某个 group 内某个属性的类型和值，relation_type和relation_val是与该属性所在的 group 相邻的 group 中与之有关系的属性的类型和值。同样，线索 10、11、14、15 就可以存储在 relations 数组中：

const RELATION relations[] = 
{{ type_cigaret, CIGARET_BLENDS, type_pet, PET_CAT },{ type_pet, PET_HORSE, type_cigaret, CIGARET_DUNHILL },{ type_nation, NATION_NORWAY, type_house, COLOR_BLUE },{ type_cigaret, CIGARET_BLENDS, type_drink, DRINK_WATER }
};

对于第三类线索，无法建立统一的数学模型

搜索算法的实现

与其他穷举类算法一样，本问题的穷举法的实现也包含两个典型过程，一个是对所有状态的穷举过程，另一个是对状态的正确判定过程。本问题的穷举搜索过程明显比之前的几个题目复杂，因为每个状态有 5 个类型，每个类型都要对 5 个值进行排列组合。

枚举所有状态

状态遍历算法的具体思路就是按照 group 中的元素顺序，依次确定状态二维表中各个元素的值。首先对房子根据颜色组合进行穷举，每得到一组房子颜色组合后，记录到状态二维表的第一列，然后在此基础上对住在房子里的人的国籍进行穷举，将国籍的穷举结果记录到二维状态表的第二列，同时将国籍穷举得到的集合与房子颜色的结果做排列组合，并在这个组合结果的基础上，继续对饮料类型进行穷举和排列组合。以此类推，直到穷举完最后一种类型得到完整的状态二维表。其遍历组合的过程如下图所示，在这么多组合的结果中，只有蓝色的那一个组合结果才完全符合题目的要求，是一个正确的结果。

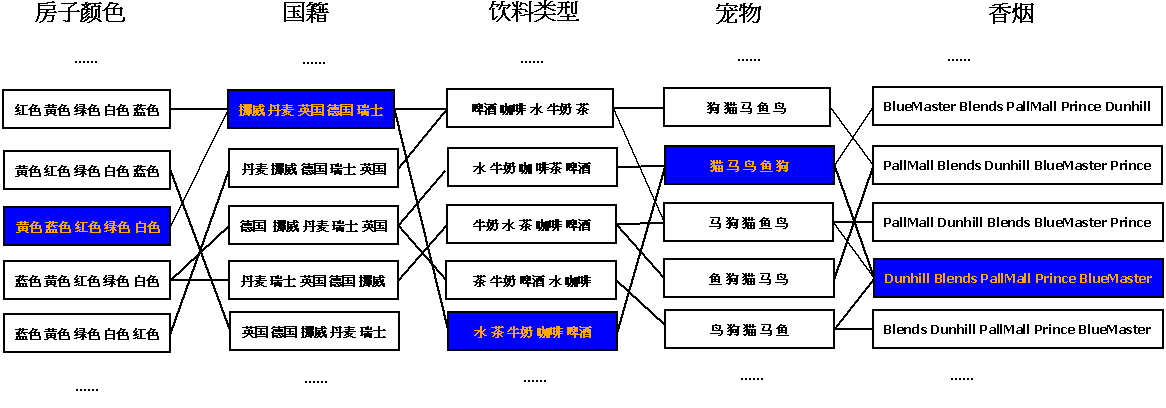
5 间房子、5 种颜色，全排列共有 $P_5^5=120 $种排列方式。像这种 n 个属性进行全排列常用的算法实现方式有两种，一种是用 n 重循环方式，另一种是用递归方式。

ArrangeHouseColors()函数中的 5 重 for 循环可以看作是 n 重循环方式的一个模板

/* 遍历房子颜色*/
void ArrangeHouseColors(GROUP *groups)
{for (int i = COLOR_BLUE; i <= COLOR_WHITE; i++){for (int j = COLOR_BLUE; j <= COLOR_WHITE; j++){if (j == i)continue;for (int k = COLOR_BLUE; k <= COLOR_WHITE; k++){if ((k == i) || (k == j))continue;for (int p = COLOR_BLUE; p <= COLOR_WHITE; p++){if ((p == i) || (p == j) || (p == k))continue;for (int q = COLOR_BLUE; q <= COLOR_WHITE; q++){if ((q == i) || (q == j) || (q == k) || (q == p))continue;groups[0].itemValue[type_house] = i;groups[1].itemValue[type_house] = j;groups[2].itemValue[type_house] = k;groups[3].itemValue[type_house] = p;groups[4].itemValue[type_house] = q;for (int groupIdx = 0; groupIdx < (GROUPS_COUNT - 1); groupIdx++){if ((groups[groupIdx].itemValue[type_house] == COLOR_GREEN)&& (groups[groupIdx + 1].itemValue[type_house] == COLOR_WHITE)){ArrangeHouseNations(groups);}}}}}}}
}

arrangeHouseNations() 函数对 5 个人的国籍进行全排列，但是这里有个特殊规则，就是“挪威人住在第一个房子里面”，实际上限制了第一个房子的人的国籍，因此只需要对剩下的四个房子和四种国籍进行 P 4 4 = 24 P_4^4=24 P44​=24 种排列即可。

/*遍历国家*/
void ArrangeHouseNations(GROUP *groups)
{/*应用规则(9)：挪威人住在第一个房子里面；*/groups[0].itemValue[type_nation] = NATION_NORWAY;for (int i = NATION_DANMARK; i <= NATION_GERMANY; i++){for (int j = NATION_DANMARK; j <= NATION_GERMANY; j++){if (j == i)continue;for (int k = NATION_DANMARK; k <= NATION_GERMANY; k++){if ((k == i) || (k == j))continue;for (int p = NATION_DANMARK; p <= NATION_GERMANY; p++){if ((p == i) || (p == j) || (p == k))continue;groups[1].itemValue[type_nation] = i;groups[2].itemValue[type_nation] = j;groups[3].itemValue[type_nation] = k;groups[4].itemValue[type_nation] = p;ArrangePeopleDrinks(groups);}}}}
}

ArrangePeopleDrinks()函数对 5 种饮料进行全排列枚举，对饮料的排列也有一个特殊规则，即“住在中间房子里的人喝牛奶”。

void ArrangePeopleDrinks(GROUP *groups)
{/*应用规则(8)：住在中间那个房子里的人喝牛奶；*/groups[2].itemValue[type_drink] = DRINK_MILK;for (int i = DRINK_TEA; i <= DRINK_BEER; i++){for (int j = DRINK_TEA; j <= DRINK_BEER; j++){if (j == i)continue;for (int k = DRINK_TEA; k <= DRINK_BEER; k++){if ((k == i) || (k == j))continue;for (int p = DRINK_TEA; p <= DRINK_BEER; p++){if ((p == i) || (p == j) || (p == k))continue;groups[0].itemValue[type_drink] = i;groups[1].itemValue[type_drink] = j;groups[3].itemValue[type_drink] = k;groups[4].itemValue[type_drink] = p;ArrangePeoplePet(groups);}}}}
}

对宠物和对香烟品牌的枚举没有特殊规则需要处理，都是直接 5 重循环，最后枚举完香烟品牌后，就得到了一个完整的二维状态表，接下来就是调用 DoGroupsfinalCheck() 函数对结果做最后的检查。

void ArrangePeopleCigert(GROUP *groups)
{/*这里没有可用规则*/for (int i = CIGARET_BLENDS; i <= CIGARET_BLUEMASTER; i++){for (int j = CIGARET_BLENDS; j <= CIGARET_BLUEMASTER; j++){if (j == i)continue;for (int k = CIGARET_BLENDS; k <= CIGARET_BLUEMASTER; k++){if ((k == i) || (k == j))continue;for (int p = CIGARET_BLENDS; p <= CIGARET_BLUEMASTER; p++){if ((p == i) || (p == j) || (p == k))continue;for (int q = CIGARET_BLENDS; q <= CIGARET_BLUEMASTER; q++){if ((q == i) || (q == j) || (q == k) || (q == p))continue;groups[0].itemValue[type_cigaret] = i;groups[1].itemValue[type_cigaret] = j;groups[2].itemValue[type_cigaret] = k;groups[3].itemValue[type_cigaret] = p;groups[4].itemValue[type_cigaret] = q;DoGroupsfinalCheck(groups);}}}}}
}void ArrangePeoplePet(GROUP *groups)
{/*这里没有可用规则*/for (int i = PET_HORSE; i <= PET_DOG; i++){for (int j = PET_HORSE; j <= PET_DOG; j++){if (j == i)continue;for (int k = PET_HORSE; k <= PET_DOG; k++){if ((k == i) || (k == j))continue;for (int p = PET_HORSE; p <= PET_DOG; p++){if ((p == i) || (p == j) || (p == k))continue;for (int q = PET_HORSE; q <= PET_DOG; q++){if ((q == i) || (q == j) || (q == k) || (q == p))continue;groups[0].itemValue[type_pet] = i;groups[1].itemValue[type_pet] = j;groups[2].itemValue[type_pet] = k;groups[3].itemValue[type_pet] = p;groups[4].itemValue[type_pet] = q;ArrangePeopleCigert(groups);}}}}}
}

状态正确性判断

通过前面“线索模型定义”的分析，将 15 条解题信息分为三类，其中第三类线索已经融入到枚举过程中了，因此判断结果的正确性只需要用第一类线索和第二类线索进行过滤即可。

void DoGroupsfinalCheck(GROUP *groups)
{ if(CheckAllGroupsBind(groups, binds) && CheckAllGroupsRelation(groups, relations)){PrintAllGroupsResult(groups, GROUPS_COUNT);}
}

CheckAllGroupsBind() 函数负责对绑定关系进行检查，for 循环遍历所有的绑定关系，只要 FindGroupIdxByItem()发现某个组里有符合 first_type 和 first_val 的属性，就立即检查其 second_type 对应属性的值是否与绑定关系中要求的 second_val 一致。以第一条绑定规则为例（英国人住在红色的房子里）：

{ type_house, COLOR_RED, type_nation, NATION_ENGLAND }

只要 FindGroupIdxByItem() 发现某个组匹配了第一个类型和值，即：

group[x].itemValue[type_house] == COLOR_RED

就会检查其 type_nation 属性的值是否是 NATION_ENGLAND，即：

group[x].itemValue[type_nation] == NATION_ENGLAND ？？？

bool CheckGroupBind(GROUP *groups, int groupIdx, ITEM_TYPE type, int value)
{if(GetGroupItemValue(&groups[groupIdx], type) != value){return false;}return true;
}bool CheckAllGroupsBind(GROUP *groups, const BIND *binds)
{for(int i = 0; i < BINDS_COUNT; i++){int grpIdx = FindGroupIdxByItem(groups, binds[i].first_type, binds[i].first_val);if(grpIdx != -1){if(!CheckGroupBind(groups, grpIdx, binds[i].second_type, binds[i].second_val)){return false;}}}return true;
}

第二类线索是 group 之间的相邻关系线索，描述的是相邻的两个 group 之间的属性的固定关系

CheckAllGroupsRelation()函数负责对关联关系进行检查，for 循环遍历所有的关联关系，只要 FindGroupIdxByItem() 函数发现某个组中有关联关系匹配的类型和值（类型和值必须都匹配），就检查这个组的前一个组和后一个组是否有匹配第二个类型和值的情况，如果有则满足关联关系，否则不满足关联关系。代码中为了避免越界，CheckGroupRelation() 函数对第一个组和最后一个组的情况做了特殊处理，当 groupIdx == 0 的时候，只检查后面的一组，当 groupIdx == (GROUPS_COUNT - 1)的时候，只检查前面的一组。

bool CheckGroupRelation(GROUP *groups, int groupIdx, ITEM_TYPE type, int value)
{if(groupIdx == 0){    //只检查后一个组if(GetGroupItemValue(&groups[groupIdx + 1], type) != value){return false;}}else if(groupIdx == (GROUPS_COUNT - 1)){    //只检查前一个组if(GetGroupItemValue(&groups[groupIdx - 1], type) != value){return false;}}else{    //检查前后两个组if( (GetGroupItemValue(&groups[groupIdx - 1], type) != value)&& (GetGroupItemValue(&groups[groupIdx + 1], type) != value) ){return false;}}return true;
}bool CheckAllGroupsRelation(GROUP *groups, const RELATION *relations)
{for(int i = 0; i < RELATIONS_COUNT; i++){int grpIdx = FindGroupIdxByItem(groups, relations[i].type, relations[i].val);if(grpIdx != -1){if(!CheckGroupRelation(groups, grpIdx, relations[i].relation_type, relations[i].relation_val)){return false;}}}return true;
}

同样以第一条关联规则为例（抽 Blends 牌香烟的人和养猫的人相邻）：

{ type_cigaret, CIGARET_BLENDS, type_pet, PET_CAT }

首先由只要 FindGroupIdxByItem() 发现某个组匹配了抽牌子香烟的人：

if(group[groupIdx].itemValue[type_cigaret] == CIGARET_BLENDS)
{//...
}

就会检查其相邻的 group 是否匹配关联关系中要求的类型和值，即检查：

group[groupIdx-1].itemValue[type_pet] ？= PET_CAT
group[groupIdx+1].itemValue[type_pet] ？= PET_CAT

总结

有将近两亿个组合结果，看来出现多个正确答案的可能性很大哟。但是，令人惊讶的是竟然只有一组结果能通过所有的线索检查，就是前面给出的答案。这个结果有点出乎预料，但是也从侧面说明了这个问题的难度。另外，对大约两亿个状态的穷举和检查需要耗时约 5s，这也体现了穷举法应用的一些局限性，就是当问题规模比较大时，穷举法是一个低效的方法。对于更大规模的问题，应尽量避免使用穷举法。

完整代码

#include <cassert>const int GROUPS_ITEMS = 5;
const int GROUPS_COUNT = 5;const int COLOR_BLUE    = 0;
const int COLOR_RED     = 1;
const int COLOR_GREEN   = 2;
const int COLOR_YELLOW  = 3;
const int COLOR_WHITE   = 4;const int NATION_NORWAY     = 0;
const int NATION_DANMARK    = 1;
const int NATION_SWEDEND    = 2;
const int NATION_ENGLAND    = 3;
const int NATION_GERMANY    = 4;const int DRINK_TEA     = 0;
const int DRINK_WATER   = 1;
const int DRINK_COFFEE  = 2;
const int DRINK_BEER    = 3;
const int DRINK_MILK    = 4;const int PET_HORSE   = 0;
const int PET_CAT     = 1;
const int PET_BIRD    = 2;
const int PET_FISH    = 3;
const int PET_DOG     = 4;const int CIGARET_BLENDS      = 0;
const int CIGARET_DUNHILL     = 1;
const int CIGARET_PRINCE      = 2;
const int CIGARET_PALLMALL    = 3;
const int CIGARET_BLUEMASTER  = 4;typedef enum 
{type_house = 0,type_nation = 1,type_drink = 2,type_pet = 3,type_cigaret = 4
}ITEM_TYPE;const char *itemName[GROUPS_ITEMS] = { "房子", "国家", "饮料", "宠物", "烟"};
const char *valueName[GROUPS_ITEMS][GROUPS_COUNT] = 
{ { "蓝色", "红色", "绿色", "黄色", "白色" },{ "挪威", "丹麦", "瑞典", "英国", "德国" },{ "茶", "水", "咖啡", "啤酒", "牛奶" },{ "马", "猫", "鸟", "鱼", "狗" },{ "Blends", "Dunhill", "Prince", "PallMall", "BlueMaster" }
};typedef struct 
{ITEM_TYPE type;int value;
}ITEM;typedef struct 
{ITEM_TYPE first_type;int first_val;ITEM_TYPE second_type;int second_val;
}BIND;const BIND binds[] = 
{{ type_house, COLOR_RED, type_nation, NATION_ENGLAND },{ type_nation, NATION_SWEDEND, type_pet, PET_DOG },{ type_nation, NATION_DANMARK, type_drink, DRINK_TEA },{ type_house, COLOR_GREEN, type_drink, DRINK_COFFEE },{ type_cigaret, CIGARET_PALLMALL, type_pet, PET_BIRD },{ type_house, COLOR_YELLOW, type_cigaret, CIGARET_DUNHILL },{ type_cigaret, CIGARET_BLUEMASTER, type_drink, DRINK_BEER },{ type_nation, NATION_GERMANY, type_cigaret, CIGARET_PRINCE }
};const int BINDS_COUNT = sizeof(binds) / sizeof(binds[0]);typedef struct tagRelation
{ITEM_TYPE type;int val;ITEM_TYPE relation_type;int relation_val;
}RELATION;const RELATION relations[] = 
{{ type_cigaret, CIGARET_BLENDS, type_pet, PET_CAT },{ type_pet, PET_HORSE, type_cigaret, CIGARET_DUNHILL },{ type_nation, NATION_NORWAY, type_house, COLOR_BLUE },{ type_cigaret, CIGARET_BLENDS, type_drink, DRINK_WATER }
};const int RELATIONS_COUNT = sizeof(relations) / sizeof(relations[0]);
/*
typedef struct tagGroup
{ITEM items[GROUPS_ITEMS];
}GROUP;
*/
typedef struct 
{int itemValue[GROUPS_ITEMS];
}GROUP;int GetGroupItemValue(GROUP *group, ITEM_TYPE type)
{return group->itemValue[type];
}int FindGroupIdxByItem(GROUP *groups, ITEM_TYPE type, int value)
{for(int i = 0; i < GROUPS_COUNT; i++){if(GetGroupItemValue(&groups[i], type) == value){return i;}}return -1;
}bool CheckGroupBind(GROUP *groups, int groupIdx, ITEM_TYPE type, int value)
{if(GetGroupItemValue(&groups[groupIdx], type) != value){return false;}return true;
}bool CheckAllGroupsBind(GROUP *groups, const BIND *binds)
{for(int i = 0; i < BINDS_COUNT; i++){int grpIdx = FindGroupIdxByItem(groups, binds[i].first_type, binds[i].first_val);if(grpIdx != -1){if(!CheckGroupBind(groups, grpIdx, binds[i].second_type, binds[i].second_val)){return false;}}}return true;
}bool CheckGroupRelation(GROUP *groups, int groupIdx, ITEM_TYPE type, int value)
{if(groupIdx == 0){if(GetGroupItemValue(&groups[groupIdx + 1], type) != value){return false;}}else if(groupIdx == (GROUPS_COUNT - 1)){if(GetGroupItemValue(&groups[groupIdx - 1], type) != value){return false;}}else{if( (GetGroupItemValue(&groups[groupIdx - 1], type) != value)&& (GetGroupItemValue(&groups[groupIdx + 1], type) != value) ){return false;}}return true;
}bool CheckAllGroupsRelation(GROUP *groups, const RELATION *relations)
{for(int i = 0; i < RELATIONS_COUNT; i++){int grpIdx = FindGroupIdxByItem(groups, relations[i].type, relations[i].val);if(grpIdx != -1){if(!CheckGroupRelation(groups, grpIdx, relations[i].relation_type, relations[i].relation_val)){return false;}}}return true;
}void PrintGroupsNameTitle()
{for(int i = type_house; i <= type_cigaret; i++){printf("%-15s", itemName[i]);}printf("\n");
}void PrintSingleLineGroup(GROUP *group)
{for(int i = type_house; i <= type_cigaret; i++){printf("%-15s", valueName[i][group->itemValue[i]]);}printf("\n");
}void PrintAllGroupsResult(GROUP *groups, int groupCount)
{PrintGroupsNameTitle();for(int i = 0; i < groupCount; i++){PrintSingleLineGroup(&groups[i]);}printf("\n");
}static int cnt = 0;
void DoGroupsfinalCheck(GROUP *groups)
{cnt++;if((cnt % 1000000) == 0)printf("%d\n", cnt);if(CheckAllGroupsBind(groups, binds) && CheckAllGroupsRelation(groups, relations)){PrintAllGroupsResult(groups, GROUPS_COUNT);}
}void ArrangePeopleCigert(GROUP *groups)
{/*这里没有可用规则*/for (int i = CIGARET_BLENDS; i <= CIGARET_BLUEMASTER; i++){for (int j = CIGARET_BLENDS; j <= CIGARET_BLUEMASTER; j++){if (j == i)continue;for (int k = CIGARET_BLENDS; k <= CIGARET_BLUEMASTER; k++){if ((k == i) || (k == j))continue;for (int p = CIGARET_BLENDS; p <= CIGARET_BLUEMASTER; p++){if ((p == i) || (p == j) || (p == k))continue;for (int q = CIGARET_BLENDS; q <= CIGARET_BLUEMASTER; q++){if ((q == i) || (q == j) || (q == k) || (q == p))continue;groups[0].itemValue[type_cigaret] = i;groups[1].itemValue[type_cigaret] = j;groups[2].itemValue[type_cigaret] = k;groups[3].itemValue[type_cigaret] = p;groups[4].itemValue[type_cigaret] = q;DoGroupsfinalCheck(groups);}}}}}
}void ArrangePeoplePet(GROUP *groups)
{/*这里没有可用规则*/for (int i = PET_HORSE; i <= PET_DOG; i++){for (int j = PET_HORSE; j <= PET_DOG; j++){if (j == i)continue;for (int k = PET_HORSE; k <= PET_DOG; k++){if ((k == i) || (k == j))continue;for (int p = PET_HORSE; p <= PET_DOG; p++){if ((p == i) || (p == j) || (p == k))continue;for (int q = PET_HORSE; q <= PET_DOG; q++){if ((q == i) || (q == j) || (q == k) || (q == p))continue;groups[0].itemValue[type_pet] = i;groups[1].itemValue[type_pet] = j;groups[2].itemValue[type_pet] = k;groups[3].itemValue[type_pet] = p;groups[4].itemValue[type_pet] = q;ArrangePeopleCigert(groups);}}}}}
}void ArrangePeopleDrinks(GROUP *groups)
{/*应用规则(8)：住在中间那个房子里的人喝牛奶；*/groups[2].itemValue[type_drink] = DRINK_MILK;for (int i = DRINK_TEA; i <= DRINK_BEER; i++){for (int j = DRINK_TEA; j <= DRINK_BEER; j++){if (j == i)continue;for (int k = DRINK_TEA; k <= DRINK_BEER; k++){if ((k == i) || (k == j))continue;for (int p = DRINK_TEA; p <= DRINK_BEER; p++){if ((p == i) || (p == j) || (p == k))continue;groups[0].itemValue[type_drink] = i;groups[1].itemValue[type_drink] = j;groups[3].itemValue[type_drink] = k;groups[4].itemValue[type_drink] = p;ArrangePeoplePet(groups);}}}}
}void ArrangeHouseNations(GROUP *groups)
{/*应用规则(9)：挪威人住在第一个房子里面；*/groups[0].itemValue[type_nation] = NATION_NORWAY;for (int i = NATION_DANMARK; i <= NATION_GERMANY; i++){for (int j = NATION_DANMARK; j <= NATION_GERMANY; j++){if (j == i)continue;for (int k = NATION_DANMARK; k <= NATION_GERMANY; k++){if ((k == i) || (k == j))continue;for (int p = NATION_DANMARK; p <= NATION_GERMANY; p++){if ((p == i) || (p == j) || (p == k))continue;groups[1].itemValue[type_nation] = i;groups[2].itemValue[type_nation] = j;groups[3].itemValue[type_nation] = k;groups[4].itemValue[type_nation] = p;ArrangePeopleDrinks(groups);}}}}
}/* 遍历房子颜色*/
void ArrangeHouseColors(GROUP *groups)
{for (int i = COLOR_BLUE; i <= COLOR_WHITE; i++){for (int j = COLOR_BLUE; j <= COLOR_WHITE; j++){if (j == i)continue;for (int k = COLOR_BLUE; k <= COLOR_WHITE; k++){if ((k == i) || (k == j))continue;for (int p = COLOR_BLUE; p <= COLOR_WHITE; p++){if ((p == i) || (p == j) || (p == k))continue;for (int q = COLOR_BLUE; q <= COLOR_WHITE; q++){if ((q == i) || (q == j) || (q == k) || (q == p))continue;groups[0].itemValue[type_house] = i;groups[1].itemValue[type_house] = j;groups[2].itemValue[type_house] = k;groups[3].itemValue[type_house] = p;groups[4].itemValue[type_house] = q;for (int groupIdx = 0; groupIdx < (GROUPS_COUNT - 1); groupIdx++){if ((groups[groupIdx].itemValue[type_house] == COLOR_GREEN)&& (groups[groupIdx + 1].itemValue[type_house] == COLOR_WHITE)){ArrangeHouseNations(groups);}}}}}}}
}int main(int argc, char* argv[])
{GROUP groups[GROUPS_COUNT] = { { 0 } };ArrangeHouseColors(groups);return 0;
}void test_Checkfunctions()
{GROUP groups[GROUPS_COUNT] = {{COLOR_YELLOW, NATION_NORWAY, DRINK_WATER, PET_CAT, CIGARET_DUNHILL},{COLOR_BLUE, NATION_DANMARK, DRINK_TEA, PET_HORSE, CIGARET_BLENDS},{COLOR_RED, NATION_ENGLAND, DRINK_MILK, PET_BIRD, CIGARET_PALLMALL},{COLOR_GREEN, NATION_GERMANY, DRINK_COFFEE, PET_FISH, CIGARET_PRINCE},{COLOR_WHITE, NATION_SWEDEND, DRINK_BEER, PET_DOG, CIGARET_BLUEMASTER}};assert(CheckAllGroupsBind(groups, binds));assert(CheckAllGroupsRelation(groups, relations));GROUP groups2[GROUPS_COUNT] = {{COLOR_YELLOW, NATION_DANMARK, DRINK_WATER, PET_CAT, CIGARET_DUNHILL},{COLOR_BLUE, NATION_NORWAY, DRINK_TEA, PET_HORSE, CIGARET_BLENDS},{COLOR_RED, NATION_ENGLAND, DRINK_MILK, PET_BIRD, CIGARET_PALLMALL},{COLOR_GREEN, NATION_GERMANY, DRINK_COFFEE, PET_FISH, CIGARET_PRINCE},{COLOR_WHITE, NATION_SWEDEND, DRINK_BEER, PET_DOG, CIGARET_BLUEMASTER}};assert(!CheckAllGroupsBind(groups2, binds));assert(!CheckAllGroupsRelation(groups2, relations));GROUP groups3[GROUPS_COUNT] = {{COLOR_YELLOW, NATION_NORWAY, DRINK_WATER, PET_CAT, CIGARET_DUNHILL},{COLOR_BLUE, NATION_DANMARK, DRINK_TEA, PET_BIRD, CIGARET_BLENDS},{COLOR_RED, NATION_ENGLAND, DRINK_MILK, PET_HORSE, CIGARET_PALLMALL},{COLOR_GREEN, NATION_GERMANY, DRINK_COFFEE, PET_FISH, CIGARET_PRINCE},{COLOR_WHITE, NATION_SWEDEND, DRINK_BEER, PET_DOG, CIGARET_BLUEMASTER}};assert(!CheckAllGroupsBind(groups3, binds));assert(!CheckAllGroupsRelation(groups3, relations));
}/*绿房子紧挨着白房子，在白房子的左边；住在中间那个房子里的人喝牛奶；挪威人住在第一个房子里面；国家           房子           宠物           饮料           香烟挪威           黄色             猫         矿泉水        Dunhill丹麦           蓝色             马             茶         Blends英国           红色             鸟           牛奶       PallMall德国           绿色             鱼           咖啡         Prince瑞典           白色             狗           啤酒     BlueMaster
*/

这篇关于爱因斯坦思考题[超详细C++版]的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/495912。

相关文章

深入理解C++ 空类大小

深入理解C++ 空类大小

《深入理解C++空类大小》本文主要介绍了C++空类大小,规定空类大小为1字节,主要是为了保证对象的唯一性和可区分性,满足数组元素地址连续的要求,下面就来了解一下... 目录1. 保证对象的唯一性和可区分性2. 满足数组元素地址连续的要求3. 与C++的对象模型和内存管理机制相适配查看类对象内存在C++中，规
阅读更多...
最新版IDEA配置 Tomcat的详细过程

最新版IDEA配置 Tomcat的详细过程

《最新版IDEA配置Tomcat的详细过程》本文介绍如何在IDEA中配置Tomcat服务器,并创建Web项目,首先检查Tomcat是否安装完成,然后在IDEA中创建Web项目并添加Web结构,接着,... 目录配置tomcat第一步，先给项目添加Web结构查看端口号配置tomcat    先检查自己的to
阅读更多...
使用Nginx来共享文件的详细教程

使用Nginx来共享文件的详细教程

《使用Nginx来共享文件的详细教程》有时我们想共享电脑上的某些文件,一个比较方便的做法是,开一个HTTP服务,指向文件所在的目录,这次我们用nginx来实现这个需求,本文将通过代码示例一步步教你使用... 在本教程中，我们将向您展示如何使用开源 Web 服务器 Nginx 设置文件共享服务器步骤 0 —
阅读更多...
SpringBoot集成SOL链的详细过程

SpringBoot集成SOL链的详细过程

《SpringBoot集成SOL链的详细过程》Solanaj是一个用于与Solana区块链交互的Java库,它为Java开发者提供了一套功能丰富的API,使得在Java环境中可以轻松构建与Solana... 目录一、什么是solanaj?二、Pom依赖三、主要类3.1 RpcClient3.2 Public
阅读更多...
手把手教你idea中创建一个javaweb(webapp)项目详细图文教程

手把手教你idea中创建一个javaweb(webapp)项目详细图文教程

《手把手教你idea中创建一个javaweb(webapp)项目详细图文教程》：本文主要介绍如何使用IntelliJIDEA创建一个Maven项目,并配置Tomcat服务器进行运行,过程包括创建... 1.启动idea2.创建项目模板点击项目-新建项目-选择maven，显示如下页面输入项目名称，选择
阅读更多...
Python基于火山引擎豆包大模型搭建QQ机器人详细教程(2024年最新)

Python基于火山引擎豆包大模型搭建QQ机器人详细教程(2024年最新)

《Python基于火山引擎豆包大模型搭建QQ机器人详细教程(2024年最新)》：本文主要介绍Python基于火山引擎豆包大模型搭建QQ机器人详细的相关资料,包括开通模型、配置APIKEY鉴权和SD... 目录豆包大模型概述开通模型付费安装 SDK 环境配置 API KEY 鉴权Ark 模型接口Prompt
阅读更多...
在 VSCode 中配置 C++ 开发环境的详细教程

在 VSCode 中配置 C++ 开发环境的详细教程

《在VSCode中配置C++开发环境的详细教程》本文详细介绍了如何在VisualStudioCode（VSCode）中配置C++开发环境,包括安装必要的工具、配置编译器、设置调试环境等步骤,通... 目录如何在 VSCode 中配置 C++ 开发环境：详细教程1. 什么是 VSCode？2. 安装 VSCo
阅读更多...
Spring Boot 中整合 MyBatis-Plus详细步骤(最新推荐)

Spring Boot 中整合 MyBatis-Plus详细步骤(最新推荐)

《SpringBoot中整合MyBatis-Plus详细步骤(最新推荐)》本文详细介绍了如何在SpringBoot项目中整合MyBatis-Plus,包括整合步骤、基本CRUD操作、分页查询、批... 目录一、整合步骤1. 创建 Spring Boot 项目2. 配置项目依赖3. 配置数据源4. 创建实体类
阅读更多...
python与QT联合的详细步骤记录

python与QT联合的详细步骤记录

《python与QT联合的详细步骤记录》：本文主要介绍python与QT联合的详细步骤,文章还展示了如何在Python中调用QT的.ui文件来实现GUI界面,并介绍了多窗口的应用,文中通过代码介绍... 目录一、文章简介二、安装pyqt5三、GUI页面设计四、python的使用python文件创建pytho
阅读更多...
SpringBoot整合InfluxDB的详细过程

SpringBoot整合InfluxDB的详细过程

《SpringBoot整合InfluxDB的详细过程》InfluxDB是一个开源的时间序列数据库,由Go语言编写,适用于存储和查询按时间顺序产生的数据,它具有高效的数据存储和查询机制,支持高并发写入和... 目录一、简单介绍InfluxDB是什么？1、主要特点2、应用场景二、使用步骤1、集成原生的Influ
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2