NOIP2014提高组题解Day1

[NOIP2014 提高组] 生活大爆炸版石头剪刀布

题目：[NOIP2014提高组] 生活大爆炸版石头剪刀布

题目描述

石头剪刀布是常见的猜拳游戏:石头胜剪刀,剪刀胜布,布胜石头。如果两个人出拳一样，则不分胜负。在《生活大爆炸》第二季第 8 集中出现了一种石头剪刀布的升级版游戏。

升级版游戏在传统的石头剪刀布游戏的基础上,增加了两个新手势:

斯波克:《星际迷航》主角之一。

蜥蜴人:《星际迷航》中的反面角色。

这五种手势的胜负关系如表一所示,表中列出的是甲对乙的游戏结果。

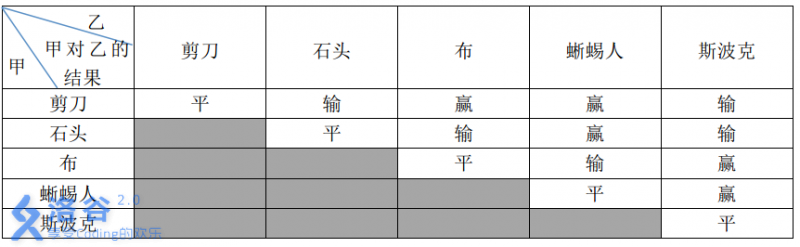
现在,小 A 和小 B 尝试玩这种升级版的猜拳游戏。已知他们的出拳都是有周期性规律的，但周期长度不一定相等。例如：如果小 A 以“石头-布-石头-剪刀-蜥蜴人-斯波克”长度为 $6$ 的周期出拳,那么他的出拳序列就是“石头-布-石头-剪刀-蜥蜴人-斯波克-石头-布-石头-剪刀-蜥蜴人-斯波克-…”,而如果小 B 以“剪刀-石头-布-斯波克-蜥蜴人”长度为 $5$ 的周期出拳,那么他出拳的序列就是“剪刀-石头-布-斯波克-蜥蜴人-剪刀-石头-布-斯波克-蜥蜴人-…”

已知小 A 和小 B 一共进行 $N$ 次猜拳。每一次赢的人得 $1$ 分，输的得 $0$ 分；平局两人都得 $0$ 分。现请你统计 $N$ 次猜拳结束之后两人的得分。

输入格式

第一行包含三个整数：$N,N_A,N_B$,分别表示共进行 $N$ 次猜拳、小 A 出拳的周期长度，小 B 出拳的周期长度。数与数之间以一个空格分隔。

第二行包含 $N_A$ 个整数,表示小 A 出拳的规律,第三行包含 $N_B$ 个整数,表示小 B 出拳的规律。其中，$0$ 表示“剪刀”，$1$ 表示“石头”，$2$ 表示“布”，$3$ 表示“蜥蜴人”，$4 $表示“斯波克”。数与数之间以一个空格分隔。

输出格式

输出一行，包含两个整数，以一个空格分隔，分别表示小 A、小 B 的得分。

样例 #1

样例输入 #1

10 5 6
0 1 2 3 4
0 3 4 2 1 0

样例输出 #1

6 2

样例 #2

样例输入 #2

9 5 5
0 1 2 3 4
1 0 3 2 4

样例输出 #2

4 4

提示

对于$100\%$的数据，$0<N\le 200,0<N_A\le 200,0<N_B\le 200$ 。

题解

解题思路

本题是一个很简单的模拟题

为了解决这个问题，我们需要模拟小 A 和小 B 进行猜拳游戏的过程，并统计他们的得分。

首先，我们将两个人的出拳规律按照周期长度扩展到 $N$ 次，然后逐次比较每一次的出拳结果，并根据规则判断谁获胜，最终得到他们的得分。

考点

模拟

时间复杂度

$O(N)$

AC代码

#pragma GCC optimize(2) 
#include <bits/stdc++.h>
using namespace std;
const int MAXN=205;
long long read(){long long ans=0,f=1;char ch=getchar();while(!isdigit(ch)){f*=(ch=='-')?-1:1;ch=getchar();}while(isdigit(ch)){ans=(ans<<1)+(ans<<3)+(ch^48);ch=getchar();}return ans*f;
}
long long n,na,nb,flagjia=1,flagyi=1,pointa,pointb;
long long jia[MAXN],yi[MAXN];
long long check(long long a,long long b){if(a==b){return 2;}//平局 if(a==0){if(b==1||b==4){return 0;}else{return 1;}}if(a==1){if(b==2||b==4){return 0;}else{return 1;}}if(a==2){if(b==0||b==3){return 0;}else{return 1;}}if(a==3){if(b==0||b==1){return 0;}else{return 1;}}if(a==4){if(b==2||b==3){return 0;}else{return 1;}}
}
int main() {n=read();na=read();nb=read();for(int i=1;i<=na;i++){jia[i]=read();}for(int i=1;i<=nb;i++){yi[i]=read();}for(int i=1;i<=n;i++){if(flagjia>na){flagjia=1;}if(flagyi>nb){flagyi=1;}if(check(jia[flagjia],yi[flagyi])==1){pointa++;}else if(!check(jia[flagjia],yi[flagyi])){pointb++;}flagjia++;flagyi++;}printf("%lld %lld",pointa,pointb);return 0;
}

---

[NOIP2014 提高组] 联合权值

题目：[NOIP2014提高组] 联合权值

题目描述

无向连通图 $G$ 有 $n$ 个点，$n-1$ 条边。点从 $1$ 到 $n$ 依次编号,编号为 $i$ 的点的权值为 $W_i$，每条边的长度均为 $1$。图上两点 $(u,v)$ 的距离定义为 $u$ 点到 $v$ 点的最短距离。对于图 $G$ 上的点对 $(u,v)$，若它们的距离为 $2$，则它们之间会产生 $W_v\times W_u$ 的联合权值。

请问图 $G$ 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入格式

第一行包含 $1$ 个整数 $n$。

接下来 $n-1$ 行,每行包含 $2$ 个用空格隔开的正整数 $u,v$，表示编号为 $u$ 和编号为 $v$ 的点之间有边相连。

最后 $1$ 行，包含 $n$ 个正整数，每两个正整数之间用一个空格隔开，其中第 $i$ 个整数表示图 $G$ 上编号为 $i$ 的点的权值为 $W_i$。

输出格式

输出共 $1$ 行，包含 $2$ 个整数，之间用一个空格隔开,依次为图 $G$ 上联合权值的最大值和所有联合权值之和。由于所有联合权值之和可能很大，输出它时要对 $10007$ 取余。

样例 #1

样例输入 #1

5  
1 2  
2 3
3 4  
4 5  
1 5 2 3 10

样例输出 #1

20 74

提示

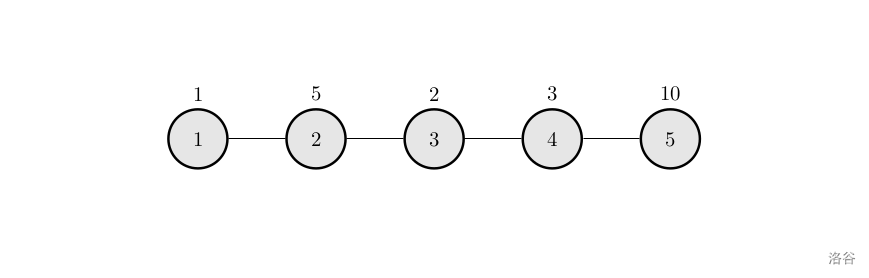
本例输入的图如上所示，距离为 $2$ 的有序点对有$(1,3)$ 、$(2,4)$ 、$(3,1)$ 、$(3,5) $、$(4,2)$ 、$(5,3) $。

其联合权值分别为 $2,15,2,20,15,20$。其中最大的是 $20$，总和为 $74$。

【数据说明】

• 对于 $30\%$ 的数据，$1<n\le 100$；
• 对于 $60\%$ 的数据，$1<n\le 2000$；
• 对于 $100\%$ 的数据，$1<n\le 2\times 10^5$，$0<W_i\le 10000$。

保证一定存在可产生联合权值的有序点对。

题解

解题思路(一)

首先，此题说的比较的隐晦。所谓的有$n-1$条边，$n$个点的无相连通图，其实就是一颗无根树。换句话说，没有一个环。所以，要是两个点同于另一个点相连，则它们不可能再有边相连，即它们之间的距离为$2$.

于是，思路就隐隐出来了：枚举每一个点，取其任意两个点，然后进行组合，然后两两相乘，得到最大值与他们的和。将所有值统计一下，然后注意因为和是组合出来的，所以再乘$2$，输出就可以了。

联合的两个节点距离为二，所以必定有一个中转点。所以，我们可以枚举每一个中转点。（震惊！！！）

假设每个中转点周围有两个点，权值分别为$a、b$，则联合权值为$2ab=(a+b{)}^2-(a^2+b^2)$。

若有三个点，权值分别为$a、b、c$，则联合权值为$2ab+2bc+2ac=(a+b+c{)}^2-(a^2+b^2+c^2)$。

综上，以某个节点为中转点的联合权值之和等于权值和的平方减去权值的平方和。（+1！！！！！）

为了找到最大的联合权值，只需找到周围最大的两个权值$max1，max2$，相乘判断即可。

注意：虽然题目让%10007，但最大联合权值是不能%10007的！！！（40分WA的看这里！！）

考点

搜索 图论

时间复杂度

$O(N)$

AC代码

#pragma GCC optimize(2) 
#include <bits/stdc++.h>
using namespace std;
long long read(){long long ans=0,f=1;char ch=getchar();while(!isdigit(ch)){f*=(ch=='-')?-1:1;ch=getchar();}while(isdigit(ch)){ans=(ans<<1)+(ans<<3)+(ch^48);ch=getchar();}return ans*f;
}
struct edge{int next;int to;
}a[400005];
int edgenum,head[200005],w[200005];
int n,ans,maxx;
void add(int u,int v){a[++edgenum].next=head[u];a[edgenum].to=v;head[u]=edgenum;
}
int main(){n=read();for(int i=1;i<n;i++){int u=read(),v=read();add(u,v);add(v,u);}for(int i=1;i<=n;i++){w[i]=read();}for(int i=1;i<=n;i++){int max1=0,max2=0;int t1=0,t2=0;for(int j=head[i];j;j=a[j].next){if(w[a[j].to]>max1){max2=max1,max1=w[a[j].to];}else if(w[a[j].to]>max2){max2=w[a[j].to];}t1=(t1+w[a[j].to])%10007;t2=(t2+w[a[j].to]*w[a[j].to])%10007;}t1=t1*t1%10007;ans=(ans+t1+10007-t2)%10007;if(maxx<max1*max2){maxx=max1*max2;}}printf("%d %d\n",maxx,ans);return 0;
}

解题思路(二)

很容易发现，这个图其实是一棵树（这看不出来就真的没谁了）

在无边权的树上随意指定一个节点为根，那么我们会发现树上距离为2的节点只有两种情况：

1.两个节点为“祖父-孙子”

2.两个节点互为兄弟

“祖父-孙子”这种情况比较好解决，在dfs便利树的时候不仅仅传递父亲$(f)$，还把祖父$(g$)一起传递

那么联合权值就为$w[r]\ast w[g]$（记录总和时要乘2）

那么我们看看兄弟情况该如何解决

设一个节点r的儿子分别是$son[1],son[2],son[3]...$

那么他们的最大值显然是$son$中最大的$w$乘上第二大的$w$

用$maf$和$mas$分别记录一下最大值和次大值就可以了

总和也很好搞，记录一下$son$中$w$总和，平方一下，再减去$son[i]$与$son[i]$（自己配自己）这样不合法的情况即可

这些都是可以在dfs时顺道完成的

所以我们的时间复杂度就是$O(n)$

至此，我们完成了这道题，如果有不懂的请看代码哦

AC代码

#pragma GCC optimize(2) 
#include <bits/stdc++.h>
#define mod 10007
#define N 200005
#define M 400005
#define int long long
using namespace std;
long long read(){long long ans=0,f=1;char ch=getchar();while(!isdigit(ch)){f*=(ch=='-')?-1:1;ch=getchar();}while(isdigit(ch)){ans=(ans<<1)+(ans<<3)+(ch^48);ch=getchar();}return ans*f;
}
int n,w[N],ans1,ans2;
int fir[N],nex[M],tar[M],cnt;
void add(int a,int b){++cnt;tar[cnt]=b;nex[cnt]=fir[a];fir[a]=cnt;
}
void dfs(int r,int f,int g){int maf=0,mas=0,sum=0,squ=0;for(int i=fir[r];i;i=nex[i]){int v=tar[i];if(v!=f){sum=(sum+w[v])%mod;squ=(squ+w[v]*w[v]%mod)%mod;if(w[v]>maf){mas=maf;maf=w[v];}else{if(w[v]>mas){mas=w[v];} }dfs(v,r,f);}}ans1=max(ans1,max(mas*maf,w[r]*w[g]));ans2=(ans2+(sum*sum%mod-squ+mod)%mod+w[r]*w[g]*2%mod)%mod;
}
signed main(){n=read();for(int i=1;i<n;i++){int a=read(),b=read();add(a,b);add(b,a);}for(int i=1;i<=n;i++){w[i]=read();}dfs(1,0,0);printf("%lld %lld\n",ans1,ans2);return 0;
}

---

[NOIP2014 提高组] 飞扬的小鸟

题目描述

Flappy Bird 是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度，让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话，便宣告失败。

为了简化问题，我们对游戏规则进行了简化和改编:

游戏界面是一个长为 $n$，高为 $m$ 的二维平面，其中有 $k$ 个管道（忽略管道的宽度）。

小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发，到达游戏界面最右边时，游戏完成。

小鸟每个单位时间沿横坐标方向右移的距离为 $1$，竖直移动的距离由玩家控制。如果点击屏幕，小鸟就会上升一定高度 $x$，每个单位时间可以点击多次，效果叠加；如果不点击屏幕，小鸟就会下降一定高度 $y$。小鸟位于横坐标方向不同位置时，上升的高度 $x$ 和下降的高度 $y$ 可能互不相同。

小鸟高度等于 $0$ 或者小鸟碰到管道时，游戏失败。小鸟高度为 $m$ 时，无法再上升。

现在,请你判断是否可以完成游戏。如果可以，输出最少点击屏幕数；否则，输出小鸟最多可以通过多少个管道缝隙。

输入格式

第 $1$ 行有 $3$ 个整数 $n,m,k$，分别表示游戏界面的长度，高度和水管的数量，每两个整数之间用一个空格隔开；

接下来的 $n$ 行，每行 $2$ 个用一个空格隔开的整数 $x$ 和 $y$，依次表示在横坐标位置 $0\sim n-1$ 上玩家点击屏幕后，小鸟在下一位置上升的高度 $x$，以及在这个位置上玩家不点击屏幕时，小鸟在下一位置下降的高度 $y$。

接下来 $k$ 行，每行 $3$ 个整数 $p,l,h$，每两个整数之间用一个空格隔开。每行表示一个管道，其中 $p$ 表示管道的横坐标，$l$ 表示此管道缝隙的下边沿高度，$h$ 表示管道缝隙上边沿的高度（输入数据保证 $p$ 各不相同，但不保证按照大小顺序给出）。

输出格式

共两行。

第一行，包含一个整数，如果可以成功完成游戏，则输出 $1$，否则输出 $0$。

第二行，包含一个整数，如果第一行为 $1$，则输出成功完成游戏需要最少点击屏幕数，否则，输出小鸟最多可以通过多少个管道缝隙。

样例 #1

样例输入 #1

10 10 6 
3 9  
9 9  
1 2  
1 3  
1 2  
1 1  
2 1  
2 1  
1 6  
2 2  
1 2 7 
5 1 5 
6 3 5 
7 5 8 
8 7 9 
9 1 3

样例输出 #1

1
6

样例 #2

样例输入 #2

10 10 4 
1 2  
3 1  
2 2  
1 8  
1 8  
3 2  
2 1  
2 1  
2 2  
1 2  
1 0 2 
6 7 9 
9 1 4 
3 8 10

样例输出 #2

0
3

提示

【输入输出样例说明】

如下图所示，蓝色直线表示小鸟的飞行轨迹，红色直线表示管道。

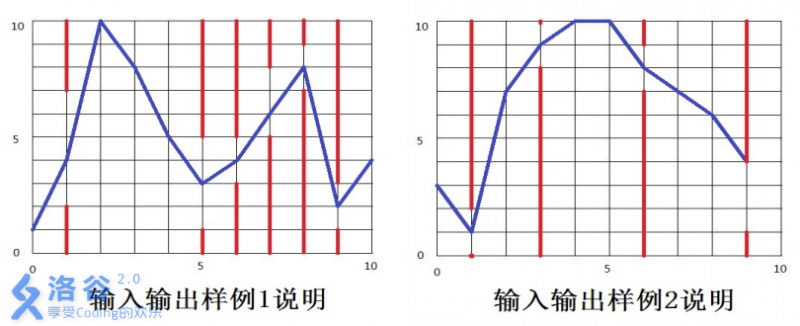
【数据范围】

对于 $30\%$ 的数据：$5\le n\le 10,5\le m\le 10,k=0$，保证存在一组最优解使得同一单位时间最多点击屏幕 $3$ 次；

对于 $50\%$ 的数据：$5\le n\le 20,5\le m\le 10$，保证存在一组最优解使得同一单位时间最多点击屏幕 $3$ 次；

对于 $70\%$ 的数据：$5\le n\le 1000,5\le m\le 100$；

对于 $100\%$ 的数据：$5\le n\le 10000$，$5\le m\le 1000$，$0\le k<n$，$0<x,y<m$，$0<p<n$，$0\le l<h\le m$， $l+1<h$。

题解

解题思路

恩，这题是一道背包。就是说小鸟在往上飞的时候是完全背包，然后往下掉的时候是01背包。

为了不冲突，就是先做完全，然后再做01，最后将不合法的剔除。

这道题是一个动态规划问题，需要确定状态和状态转移方程。

首先，我们可以定义一个二维数组$dp[i][j]$，表示小鸟到达位置$(i,j)$时的最小点击次数。其中，$i$表示横坐标位置，取值范围为$0$到$n$，$j$表示小鸟的高度，取值范围为$0$到$m$。

状态转移方程如下：

当j不等于$m$时（小鸟不在最大高度），$dp[i][j]$的值可以通过以下两种方式得到：

小鸟在当前位置$(i,j)$点击屏幕，上升到高度$j+x[i]$，此时的点击次数为$dp[i-1][j+x[i]]+1$。
小鸟在上一个位置$(i-1,j)$点击屏幕，上升到高度$j+x[i-1]$，然后下降到高度$j$，此时的点击次数为$dp[i-1][j+x[i-1]]+1$。
所以，$dp[i][j]$的值为上述两种方式中的较小值。
当j等于$m$时（小鸟在最大高度），$dp[i][j]$的值可以通过以下两种方式得到：

小鸟在当前位置$(i,j)$点击屏幕，上升到高度$j+x[i]$，此时的点击次数为$dp[i-1][j+x[i]]+1$。
小鸟在上一个位置$(i-1,j)$点击屏幕，上升到高度$j+x[i-1]$，然后下降到高度j，此时的点击次数为$dp[i-1][j+x[i-1]]+1$。

所以，$dp[i][j]$的值为上述两种方式中的较小值。

对于管道的处理：

如果当前位置$(i,j)$处有管道，即$p[i]$为$true$，则将管道的数量$k$减$1$。

在状态转移方程中，当计算$dp[i][j]$的值时，只考虑在管道缝隙内部的高度范围，即$l[i]+1$到$h[i]-1$之间的高度。

最后，遍历最后一行$dp[n][j]$，找到其中的最小值$ans$，即为小鸟成功完成游戏所需的最少点击次数。如果$ans$小于一个极大值$MAXDP$，则输出$1$和$ans$；否则，输出$0$和原始管道数量$k$。

考点

动态规划,dp 枚举 背包

时间复杂度

$O(N{M}^2)$

AC代码

#pragma GCC optimize(2) 
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int MAXDP=200005;
long long read(){long long ans=0,f=1;char ch=getchar();while(!isdigit(ch)){f*=(ch=='-')?-1:1;ch=getchar();}while(isdigit(ch)){ans=(ans<<1)+(ans<<3)+(ch^48);ch=getchar();}return ans*f;
}
int l[10010],h[10010];
int dp[10010][1010];
int x[10010],y[10010];
bool p[10010];
signed main(){int n,i,j,k,m,w;n=read();m=read();k=read();for(i=0;i<n;i++){x[i]=read();y[i]=read();l[i]=0;h[i]=m+1;}l[n]=0;h[n]=m+1;for(i=0;i<k;i++){w=read();l[w]=read();h[w]=read();p[w]=true;}for(i=1;i<=n;i++){for(j=0;j<=m;j++){dp[i][j]=MAXDP;}}dp[0][0]=MAXDP;for(i=1;i<=m;i++){dp[0][i]=0;}for(i=1;i<=n;i++){for(j=x[i-1];j<=m;j++){if(j==m){for(w=m-x[i-1];w<=m;w++){dp[i][j]=min(dp[i][j],dp[i-1][w]+1);dp[i][j]=min(dp[i][j],dp[i][w]+1);}}dp[i][j]=min(dp[i][j],dp[i-1][j-x[i-1]]+1);dp[i][j]=min(dp[i][j],dp[i][j-x[i-1]]+1);}for(j=max((long long)1,l[i]+1);j<=min(m-y[i-1],h[i]-1);j++){dp[i][j]=min(dp[i][j],dp[i-1][j+y[i-1]]);}for(j=l[i];j>=1;j--){dp[i][j]=MAXDP;}for(j=h[i];j<=m;j++){dp[i][j]=MAXDP;}}int ans=MAXDP;int cnt=k;for(i=n;i>=1;i--){for(j=l[i]+1;j<=h[i]-1;j++){ans=min(ans,dp[i][j]);}if(ans<MAXDP){break;}if(p[i]==true){k--;}    }if(cnt==k){printf("1\n%lld",ans);}else{printf("0\n%lld",k);}return 0;
}

---